Time in physics - AbsoluteAstronomy.com

Time in physics is defined by its measurement

Operational definition

An operational definition defines something in terms of the specific process or set of validation tests used to determine its presence and quantity. That is, one defines something in terms of the operations that count as measuring it. The term was coined by Percy Williams Bridgman and is a part of...

: time is what a clock

Clock

A clock is an instrument used to indicate, keep, and co-ordinate time. The word clock is derived ultimately from the Celtic words clagan and clocca meaning "bell". A silent instrument missing such a mechanism has traditionally been known as a timepiece...

reads. It is a scalar

Scalar (physics)

In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...

quantity and, like length

Length

In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...

, mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

, and charge

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

, is usually described as a fundamental quantity. Time can be combined mathematically with other physical quantities to derive

Derive

Derive may refer to:*Derive , a commercial computer algebra system made by Texas Instruments*Dérive, the spontaneous exploration of urban landscapes guided by aesthetic instinct....

other concepts such as motion

Motion (physics)

In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...

, kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

and time-dependent fields

Field (physics)

In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...

. Timekeeping is a complex of technological and scientific issues, and part of the foundation of recordkeeping.
! scientific notation

Scientific notation

Scientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...

|-
! natural units

Natural units

In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...

|-
! algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

|-
! geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

|-
! vector notation

Vector notation

This page is an overview of the common notations used when working with vectors, which may be spatial or more abstract members of vector spaces....

|-
! optics

Optics

Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...

|-
! operators
|-
! differential equations
|-
! partial differential equations
|-
! electrical engineering

Electrical engineering

Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...

|-
! signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

Markers of time

Before there were clocks, time was measured by those physical processes which were understandable to each epoch of civilization:

the first appearance (see: heliacal rising
Heliacal rising
The heliacal rising of a star occurs when it first becomes visible above the eastern horizon for a brief moment just before sunrise, after a period of time when it had not been visible....

) of Sirius
Sirius
Sirius is the brightest star in the night sky. With a visual apparent magnitude of −1.46, it is almost twice as bright as Canopus, the next brightest star. The name "Sirius" is derived from the Ancient Greek: Seirios . The star has the Bayer designation Alpha Canis Majoris...

to mark the flooding of the Nile
Flooding of the Nile
has been an important natal cycle in Egypt since ancient times. It is celebrated by Egyptians as an annual holiday for two weeks starting August 15, known as Wafaa El-Nil. It is also celebrated in the Coptic Church by ceremonially throwing a martyr's relic into the river, hence the name, Esba`...

each year
the periodic succession of night
Night
Night or nighttime is the period of time when the sun is below the horizon. This occurs after dusk. The opposite of night is day...

and day
Day
A day is a unit of time, commonly defined as an interval equal to 24 hours. It also can mean that portion of the full day during which a location is illuminated by the light of the sun...

, one after the other, in seemingly eternal succession
the position on the horizon of the first appearance of the sun at dawn
the position of the sun in the sky
the marking of the moment of noon
Noon
Noon is usually defined as 12 o'clock in the daytime. The word noon is also used informally to mean midday regarding the location of the sun not the middle of a persons day. Although this is a time around the middle of the day when people in many countries take a lunch break...

time during the day
the length of the shadow cast by a gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....

Eventually, it became possible to characterize the passage of time with instrumentation, using operational definition

Operational definition

s. Simultaneously, our conception of time has evolved, as shown below.

The unit of measurement of time: the second

In the International System of Units

International System of Units

The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...

(SI), the unit of time is the second

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

(symbol:

). It is a SI base unit

SI base unit

The International System of Units defines seven units of measure as a basic set from which all other SI units are derived. These SI base units and their physical quantities are:* metre for length...

, and it is currently defined as "the duration of periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium

Caesium

Caesium or cesium is the chemical element with the symbol Cs and atomic number 55. It is a soft, silvery-gold alkali metal with a melting point of 28 °C , which makes it one of only five elemental metals that are liquid at room temperature...

133 atom."

The state of the art in timekeeping

! Measurement

Measurement

Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...

|-
! Scientific notation

Scientific notation

|-
! Natural units

Natural units

The UTC

Coordinated Universal Time

Coordinated Universal Time is the primary time standard by which the world regulates clocks and time. It is one of several closely related successors to Greenwich Mean Time. Computer servers, online services and other entities that rely on having a universally accepted time use UTC for that purpose...

timestamp

Timestamp

A timestamp is a sequence of characters, denoting the date or time at which a certain event occurred. A timestamp is the time at which an event is recorded by a computer, not the time of the event itself...

in use worldwide is an atomic time standard. The relative accuracy of such a time standard is currently on the order of 10⁻¹⁵ (corresponding to 1 second in approximately 30 million years). The smallest time step considered observable is called the Planck time

Planck time

In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...

, which is approximately 5.391×10⁻⁴⁴ seconds - many orders of magnitude below the resolution of current time standards.

Conceptions of time

Both Galileo and Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

and most people up until the 20th century thought that time was the same for everyone everywhere. This is the basis for timelines, where time is a parameter

Parameter

Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....

. Our modern conception of time is based on Einstein

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

's theory of relativity

Theory of relativity

The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....

, in which rates of time run differently depending on relative motion, and space

Space

Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...

and time are merged into spacetime

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

, where we live on a world line

World line

In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...

rather than a timeline. Thus time is part of a coordinate, in this view. Physicists believe the entire Universe

Universe

The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...

and therefore time itself began about 13.7 billion years ago in the big bang

Big Bang

The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...

. (See Time in Cosmology below) Whether it will ever come to an end is an open question. (See philosophy of physics

Philosophy of physics

In philosophy, the philosophy of physics studies the fundamental philosophical questions underlying modern physics, the study of matter and energy and how they interact. The philosophy of physics begins by reflecting on the basic metaphysical and epistemological questions posed by physics:...

Regularities in nature

In order to measure time, one can record the number of occurrences (events) of some periodic

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

phenomenon

Phenomenon

A phenomenon , plural phenomena, is any observable occurrence. Phenomena are often, but not always, understood as 'appearances' or 'experiences'...

. The regular recurrences of the seasons, the motion

Motion (physics)

s of the sun

Sun

The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

, moon

Moon

The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...

and star

Star

A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...

s were noted and tabulated for millennia, before the laws of physics were formulated. The sun was the arbiter of the flow of time, but time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

was known only to the hour

Hour

The hour is a unit of measurement of time. In modern usage, an hour comprises 60 minutes, or 3,600 seconds...

for millennia

Millennium

A millennium is a period of time equal to one thousand years —from the Latin phrase , thousand, and , year—often but not necessarily related numerically to a particular dating system....

, hence, the use of the gnomon

Gnomon

The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....

was known across most of the world, especially Eurasia

Eurasia

Eurasia is a continent or supercontinent comprising the traditional continents of Europe and Asia ; covering about 52,990,000 km2 or about 10.6% of the Earth's surface located primarily in the eastern and northern hemispheres...

, and at least as far southward as the jungles of Southeast Asia

Southeast Asia

Southeast Asia, South-East Asia, South East Asia or Southeastern Asia is a subregion of Asia, consisting of the countries that are geographically south of China, east of India, west of New Guinea and north of Australia. The region lies on the intersection of geological plates, with heavy seismic...

I farm the land from which I take my food.

I watch the sun rise and sun set.

Kings can ask no more.

--Ancient Chinese Proverb, 3500 years ago.

In particular, the astronomical observatories maintained for religious purposes became accurate enough to ascertain the regular motions of the stars, and even some of the planets.

At first, timekeeping was done by hand by priests, and then for commerce, with watchmen to note time as part of their duties.
The tabulation of the equinox

Equinox

An equinox occurs twice a year, when the tilt of the Earth's axis is inclined neither away from nor towards the Sun, the center of the Sun being in the same plane as the Earth's equator...

es, the sandglass

Marine sandglass

Marine sandglass, is an ancient marine instrument employed to measure the time at sea when used as a 30 minute hourglass. It was also used together with the chip log, to measure the boat speed through the water in knots .Originally, it consisted of two glass bottles one above the other with both...

, and the water clock

Water clock

A water clock or clepsydra is any timepiece in which time is measured by the regulated flow of liquid into or out from a vessel where the amount is then measured.Water clocks, along with sundials, are likely to be the oldest time-measuring instruments, with the only exceptions...

became more and more accurate, and finally reliable. For ships at sea, boys were used to turn the sandglass

Marine sandglass

es and to call the hours.

Mechanical clocks

Richard of Wallingford

Richard of Wallingford was an English mathematician who made major contributions to astronomy/astrology and horology while serving as abbot of St Albans Abbey in Hertfordshire.-Biography:...

(1292–1336), abbot of St. Alban's abbey, famously built a mechanical clock as an astronomical orrery

Orrery

An orrery is a mechanical device that illustrates the relative positions and motions of the planets and moons in the Solar System in a heliocentric model. Though the Greeks had working planetaria, the first orrery that was a planetarium of the modern era was produced in 1704, and one was presented...

about 1330.

By the time of Richard of Wallingford, the use of ratchet

Ratchet (device)

A ratchet is a device that allows continuous linear or rotary motion in only one direction while preventing motion in the opposite direction. Because most socket wrenches today use ratcheting handles, the term "ratchet" alone is often used to refer to a ratcheting wrench, and the terms "ratchet"...

s and gear

Gear

A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....

s allowed the towns of Europe

Europe

Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...

to create mechanisms to display the time on their respective town clocks; by the time of the scientific revolution, the clocks became miniaturized enough for families to share a personal clock, or perhaps a pocket watch. At first, only kings could afford them. Pendulum clock

Pendulum clock

A pendulum clock is a clock that uses a pendulum, a swinging weight, as its timekeeping element. The advantage of a pendulum for timekeeping is that it is a resonant device; it swings back and forth in a precise time interval dependent on its length, and resists swinging at other rates...

s were widely used in the 18th and 19th century. They have largely been replaced in general use by quartz and digital clock

Digital clock

A digital clock is a type of clock that displays the time digitally, i.e. in cyphers, as opposed to an analog clock, where the time is displayed by hands. Digital clocks are often associated with electronic drives, but the "digital" description refers only to the display, not to the drive mechanism...

s. Atomic clocks can theoretically keep accurate time for millions of years. They are appropriate for standard

Standardization

Standardization is the process of developing and implementing technical standards.The goals of standardization can be to help with independence of single suppliers , compatibility, interoperability, safety, repeatability, or quality....

s and scientific use.

Galileo: the flow of time

In 1583, Galileo Galilei

Galileo Galilei

Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...

(1564–1642) discovered that a pendulum's harmonic motion

Harmonic oscillator

In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....

has a constant period, which he learned by timing the motion of a swaying lamp in harmonic motion

Harmonic motion

Harmonic motion can mean:*The motion of a Harmonic oscillator , which can be:**Simple harmonic motion**Complex harmonic motion*Keplers laws of planetary motion...

at mass

Mass (liturgy)

"Mass" is one of the names by which the sacrament of the Eucharist is called in the Roman Catholic Church: others are "Eucharist", the "Lord's Supper", the "Breaking of Bread", the "Eucharistic assembly ", the "memorial of the Lord's Passion and Resurrection", the "Holy Sacrifice", the "Holy and...

at the cathedral of Pisa

Pisa

Pisa is a city in Tuscany, Central Italy, on the right bank of the mouth of the River Arno on the Tyrrhenian Sea. It is the capital city of the Province of Pisa...

, with his pulse

Pulse

In medicine, one's pulse represents the tactile arterial palpation of the heartbeat by trained fingertips. The pulse may be palpated in any place that allows an artery to be compressed against a bone, such as at the neck , at the wrist , behind the knee , on the inside of the elbow , and near the...

.

In his Two New Sciences

Two New Sciences

The Discourses and Mathematical Demonstrations Relating to Two New Sciences was Galileo's final book and a sort of scientific testament covering much of his work in physics over the preceding thirty years.After his Dialogue Concerning the Two Chief World Systems, the Roman Inquisition had banned...

(1638), Galileo

Galileo Galilei

used a water clock

Water clock

to measure the time taken for a bronze ball to roll a known distance down an inclined plane

Inclined plane

The inclined plane is one of the original six simple machines; as the name suggests, it is a flat surface whose endpoints are at different heights. By moving an object up an inclined plane rather than completely vertical, the amount of force required is reduced, at the expense of increasing the...

; this clock was

"a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water, which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for a part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results."

Galileo's experimental setup to measure the literal flow of time, in order to describe the motion of a ball, preceded Isaac Newton

Isaac Newton

's statement in his Principia

Principia

Principia could refer to:*Philosophiae Naturalis Principia Mathematica, Isaac Newton's three-volume work containing explanations of his laws of motion and his law of universal gravitation*Principia , a stem-group coralline alga...

I do not define time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

, space

Space

, place

Location (geography)

The terms location and place in geography are used to identify a point or an area on the Earth's surface or elsewhere. The term 'location' generally implies a higher degree of can certainty than "place" which often has an ambiguous boundary relying more on human/social attributes of place identity...

and motion

Motion (physics)

, as being well known to all.

The Galilean transformation

Galilean transformation

The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...

s assume that time is the same for all reference frames

Frame of reference

A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...

Newton's physics: linear time

In or around 1665, when Isaac Newton

Isaac Newton

(1643–1727) derived the motion of objects falling under gravity, the first clear formulation for mathematical physics

Mathematical physics

Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...

of a treatment of time began: linear time, conceived as a universal clock.

Absolute, true, and mathematical time, of itself, and from its own nature flows equably without regard to anything external, and by another name is called duration: relative, apparent, and common time, is some sensible and external (whether accurate or unequable) measure of duration by the means of motion, which is commonly used instead of true time; such as an hour, a day, a month, a year.

The water clock

Water clock

mechanism described by Galileo was engineered to provide laminar flow

Laminar flow

Laminar flow, sometimes known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross currents...

of the water during the experiments, thus providing a constant flow of water for the durations of the experiments, and embodying what Newton called duration.

In this section, the relationships listed below treat time as a parameter which serves as an index

Index

Index may refer to:-Business:* Index , a defunct UK catalogue retailer formerly owned by the Littlewoods group and known as Littlewoods Index* INDEX, a market research fair in Lucknow, India* Index fund, a collective investment scheme...

to the behavior of the physical system under consideration. Because Newton's fluent

Fluent

Fluent can refer to:* fluency, in linguistics, the ability to communicate quickly.* fluent , in mathematics, a continuous function* fluent , in artificial intelligence, a condition that varies over time...

s treat a linear flow of time (what he called mathematical time), time could be considered to be a linearly varying parameter, an abstraction of the march of the hours on the face of a clock. Calendars and ship's logs could then be mapped to the march of the hours, days, months, years and centuries.
! differential equations
|-
! partial differential equations
Lagrange

Joseph Louis Lagrange

Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...

(1736–1813) would aid in the formulation of a simpler version of Newton's equations. He started with an energy term, L, named the Lagrangian in his honor, and formulated Lagrange's equations:

The dotted quantities,

denote a function which corresponds to a Newtonian fluxion

Method of Fluxions

Method of Fluxions is a book by Isaac Newton. The book was completed in 1671, and published in 1736. Fluxions is Newton's term for differential calculus...

, whereas

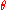denote a function which corresponds to a Newtonian fluent. But linear time is the parameter for the relationship between the

and the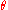

of the physical system under consideration.
Some decades later, it was found that the second order equation of Lagrange or Newton can be more easily solved or visualized by suitable transformation to sets of first order differential equations.

Lagrange's equations can be transformed, under a Legendre transformation

Legendre transformation

In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...

, to Hamilton's equations; the Hamiltonian

Hamiltonian mechanics

Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...

formulation for the equations of motion of some conjugate variables p,q (for example, momentum p and position q) is:

! Operator

Operator (physics)

In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....

s
|-
! Poisson bracket

Poisson bracket

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...

s
|-

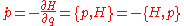
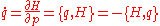
in the Poisson bracket

Poisson bracket

notation and clearly shows the dependence of the time variation of conjugate variables p,q on an energy expression.

This relationship, it was to be found, also has corresponding forms

Commutator

In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...

in quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

as well as in the classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

shown above. These relationships bespeak a conception of time which is reversible.

Thermodynamics and the paradox of irreversibility

By 1798, Benjamin Thompson

Benjamin Thompson

Sir Benjamin Thompson, Count Rumford , FRS was an American-born British physicist and inventor whose challenges to established physical theory were part of the 19th century revolution in thermodynamics. He also served as a Lieutenant-Colonel in the Loyalist forces in America during the American...

(1753–1814) had discovered that work could be transformed to heat

Heat

In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...

without limit - a precursor of the conservation of energy or

1st law of thermodynamics
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...

In 1824 Sadi Carnot

Nicolas Léonard Sadi Carnot

Nicolas Léonard Sadi Carnot was a French military engineer who, in his 1824 Reflections on the Motive Power of Fire, gave the first successful theoretical account of heat engines, now known as the Carnot cycle, thereby laying the foundations of the second law of thermodynamics...

(1796–1832) scientifically analyzed the steam engines with his Carnot cycle

Carnot cycle

The Carnot cycle is a theoretical thermodynamic cycle proposed by Nicolas Léonard Sadi Carnot in 1824 and expanded by Benoit Paul Émile Clapeyron in the 1830s and 40s. It can be shown that it is the most efficient cycle for converting a given amount of thermal energy into work, or conversely,...

, an abstract engine. Rudolf Clausius

Rudolf Clausius

Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...

(1822–1888) noted a measure of disorder, or entropy

Entropy

Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

, which affects the continually decreasing amount of free energy which is available to a Carnot engine in the:

2nd law of thermodynamics
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

Thus the continual march of a thermodynamic system, from lesser to greater entropy, at any given temperature, defines an arrow of time

Arrow of time

The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...

. In particular, Stephen Hawking

Stephen Hawking

Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...

identifies three arrows of time:

Psychological arrow of time - our perception of an inexorable flow.
Thermodynamic arrow of time - distinguished by the growth of entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

.
Cosmological arrow of time - distinguished by the expansion of the universe.

Entropy is maximum in an isolated thermodynamic system, and increases. In contrast, Erwin Schrödinger

Erwin Schrödinger

Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...

(1887–1961) pointed out that life

Life

Life is a characteristic that distinguishes objects that have signaling and self-sustaining processes from those that do not, either because such functions have ceased , or else because they lack such functions and are classified as inanimate...

depends on a "negative entropy flow". Ilya Prigogine

Ilya Prigogine

Ilya, Viscount Prigogine was a Russian-born naturalized Belgian physical chemist and Nobel Laureate noted for his work on dissipative structures, complex systems, and irreversibility.-Biography :...

(1917–2003) stated that other thermodynamic systems which, like life, are also far from equilibrium, can also exhibit stable spatio-temporal structures. Soon afterward, the Belousov-Zhabotinsky reaction

Belousov-Zhabotinsky reaction

A Belousov–Zhabotinsky reaction, or BZ reaction, is one of a class of reactions that serve as a classical example of non-equilibrium thermodynamics, resulting in the establishment of a nonlinear chemical oscillator. The only common element in these oscillating systems is the inclusion of bromine...

s were reported, which demonstrate oscillating colors in a chemical solution. These nonequilibrium thermodynamic branches reach a bifurcation point

Bifurcation theory

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...

, which is unstable, and another thermodynamic branch becomes stable in its stead.

Electromagnetism and the speed of light

In 1864, James Clerk Maxwell

James Clerk Maxwell

James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...

(1831–1879) presented a combined theory of electricity

Electricity

Electricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire...

and magnetism

Magnetism

Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...

. He combined all the laws then known relating to those two phenomenon into four equations. These vector calculus equations which use the del operator

Del

In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...

(

) are known as Maxwell's equations

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

for electromagnetism

Electromagnetism

Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...

.

In free space (that is, space not containing electric charge

Electric charge

s), the equations take the form (using SI units

International System of Units

):
! vector notation

Vector notation

This page is an overview of the common notations used when working with vectors, which may be spatial or more abstract members of vector spaces....

|-
! partial differential equations

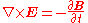
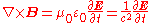
where

ε₀ and μ₀ are the electric permittivity and the magnetic permeability of free space

Vacuum permeability

The physical constant μ0, commonly called the vacuum permeability, permeability of free space, or magnetic constant is an ideal, physical constant, which is the value of magnetic permeability in a classical vacuum...

;

c =

is the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

in free space, 299 792 458 m

Metre

The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

;

E is the electric field;

B is the magnetic field.

These equations allow for solutions in the form of electromagnetic waves. The wave is formed by an electric field and a magnetic field oscillating together, perpendicular to each other and to the direction of propagation. These waves always propagate at the speed of light c, regardless of the velocity of the electric charge that generated them.

The fact that light is predicted to always travel at speed c would be incompatible with Galilean relativity if Maxwell's equations were assumed to hold in any inertial frame (reference frame with constant velocity), because the Galilean transformations predict the speed to decrease (or increase) in the reference frame of an observer traveling parallel (or antiparallel) to the light.

It was expected that there was one absolute reference frame, that of the luminiferous aether

Luminiferous aether

In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....

, in which Maxwell's equations held unmodified in the known form.

The Michelson-Morley experiment

Michelson-Morley experiment

The Michelson–Morley experiment was performed in 1887 by Albert Michelson and Edward Morley at what is now Case Western Reserve University in Cleveland, Ohio. Its results are generally considered to be the first strong evidence against the theory of a luminiferous ether and in favor of special...

failed to detect any difference in the relative speed of light due to the motion of the Earth relative to the luminiferous aether, suggesting that Maxwell's equations did, in fact, hold in all frames. In 1875, Hendrik Lorentz

Hendrik Lorentz

Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...

(1853–1928) discovered Lorentz transformation

Lorentz transformation

In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...

s, which left Maxwell's equations unchanged, allowing Michelson and Morley's negative result to be explained. Henri Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

(1854–1912) noted the importance of Lorentz' transformation and popularized it. In particular, the railroad car description can be found in Science and Hypothesis, which was published before Einstein's articles of 1905.

The Lorentz transformation predicted space contraction and time dilation

Time dilation

In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...

; until 1905, the former was interpreted as a physical contraction of objects moving with respect to the aether, due to the modification of the intermolecular forces (of electric nature), while the latter was thought to be just a mathematical stipulation.

Einstein's physics: spacetime

Main articles: special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

(1905), general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

(1915).

Albert Einstein

's 1905 special relativity

Special relativity

challenged the notion of absolute time, and could only formulate a definition of synchronization

Synchronization

Synchronization is timekeeping which requires the coordination of events to operate a system in unison. The familiar conductor of an orchestra serves to keep the orchestra in time....

for clocks that mark a linear flow of time:
Einstein showed that if the speed of light is not changing between reference frames, space and time must be so that the moving observer will measure the same speed of light as the stationary one because velocity is defined by space and time:

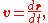where r is position and t is time.

Indeed, the Lorentz transformation (for two reference frames in relative motion, whose x axis is directed in the direction of the relative velocity)

! algebra

Algebra

|-
! trigonometry

Trigonometry

Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...

can be said to "mix" space and time in a way similar to the way a Euclidean rotation around the z axis mixes x and y coordinates. Consequences of this include relativity of simultaneity

Relativity of simultaneity

In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...

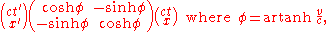More specifically, the Lorentz transformation is a hyperbolic rotation

which is a change of coordinates in the four-dimensional Minkowski space

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

, a dimension of which is ct. (In Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

an ordinary rotation

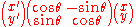is the corresponding change of coordinates.) The speed of light c can be seen as just a conversion factor needed because we measure the dimensions of spacetime in different units; since the metre

Metre

is currently defined in terms of the second, it has the exact value of . We would need a similar factor in Euclidean space if, for example, we measured width in nautical miles and depth in feet. In physics, sometimes units of measurement in which c = 1

Natural units

are used to simplify equations.

Time in a "moving" reference frame is shown to run more slowly than in a "stationary" one by the following relation (which can be derived by the Lorentz transformation by putting ∆x′ = 0, ∆τ = ∆t′):

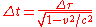
where:

∆τ is the time between two events as measured in the moving reference frame in which they occur at the same place (e.g. two ticks on a moving clock); it is called the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...

between the two events;
∆t is the time between these same two events, but as measured in the stationary reference frame;
v is the speed of the moving reference frame relative to the stationary one;
c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

.

Moving objects therefore are said to show a slower passage of time. This is known as time dilation

Time dilation

.

These transformations are only valid for two frames at constant relative velocity. Naively applying them to other situations gives rise to such paradox

Paradox

Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...

es as the twin paradox

Twin paradox

In physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...

.

That paradox can be resolved using for instance Einstein's General theory of relativity, which uses Riemannian geometry

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...

, geometry in accelerated, noninertial reference frames. Employing the metric tensor

Metric tensor

In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...

which describes Minkowski space

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

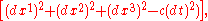
Einstein developed a geometric solution to Lorentz's transformation that preserves Maxwell's equations

Maxwell's equations

. His field equations give an exact relationship between the measurements of space and time in a given region of spacetime

Spacetime

and the energy density of that region.

Einstein's equations predict that time should be altered by the presence of gravitational fields (see the Schwarzschild metric

Schwarzschild metric

In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...

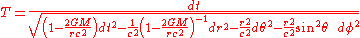
Where:

is the gravitational time dilation

Gravitational time dilation

Gravitational time dilation is the effect of time passing at different rates in regions of different gravitational potential; the lower the gravitational potential, the more slowly time passes...

of an object at a distance of

is the change in coordinate time, or the interval of coordinate time.

is the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

is the mass

Mass

generating the field

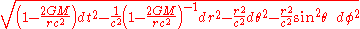is the change in proper time

Proper time

In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...

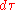, or the interval of proper time

Proper time

.

Or one could use the following simpler approximation:

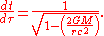
Time runs slower the stronger the gravitational field, and hence acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

, is. The predictions of time dilation are confirmed by particle acceleration

Particle accelerator

A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...

experiments and cosmic ray

Cosmic ray

Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...

evidence, where moving particles decay more slowly

Particle decay

Particle decay is the spontaneous process of one elementary particle transforming into other elementary particles. During this process, an elementary particle becomes a different particle with less mass and an intermediate particle such as W boson in muon decay. The intermediate particle then...

than their less energetic counterparts. Gravitational time dilation gives rise to the phenomenon of gravitational redshift

Gravitational redshift

In astrophysics, gravitational redshift or Einstein shift describes light or other forms of electromagnetic radiation of certain wavelengths that originate from a source that is in a region of a stronger gravitational field that appear to be of longer wavelength, or redshifted, when seen or...

and delays in signal travel time

Travel time

Travel time may refer to* Travel, movement of people between locations* Travel journal, record made by a voyager* Propagation speed, term in physics to measure things such as the speed of light or radio waves...

near massive objects such as the sun. The Global Positioning System

Global Positioning System

The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...

must also adjust signals to account for this effect.

According to Einstein's general theory of relativity, a freely moving particle traces a history in spacetime that maximises its proper time. This phenomenon is also referred to as the principle of maximal aging, and was described by Taylor

Edwin F. Taylor

Edwin F. Taylor is an American physicist known for his contributions to the teaching of physics. Taylor was editor of the American Journal of Physics, and is author of several introductory books to physics...

and Wheeler

John Archibald Wheeler

John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...

as:

"Principle of Extremal Aging: The path a free object takes between two events in spacetime is the path for which the time lapse between these events, recorded on the object's wristwatch, is an extremum."

Einstein's theory was motivated by the assumption that every point in the universe can be treated as a 'center', and that correspondingly, physics must act the same in all reference frames. His simple and elegant theory shows that time is relative to an inertial frame. In an inertial frame, Newton's first law holds; it has its own local geometry, and therefore its own measurements of space and time; there is no 'universal clock. An act of synchronization must be performed between two systems, at the least.

Time in quantum mechanics

There is a time parameter in the equations of quantum mechanics

Quantum mechanics

. The Schrödinger equation

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

is
! physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

|-
! quantum mechanics

Quantum mechanics

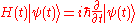
One solution can be

.
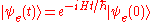where

is called the time evolution operator, and H is the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

.

But the Schrödinger picture

Schrödinger picture

In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...

shown above is equivalent to the Heisenberg picture

Heisenberg picture

In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...

, which enjoys a similarity to the Poisson brackets of classical mechanics. The Poisson bracket

Poisson bracket

s are superseded by a nonzero commutator

Commutator

, say [H,A] for observable

Observable

In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...

A, and Hamiltonian H:

This equation denotes an uncertainty relation

Uncertainty principle

In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...

in quantum physics. For example, with time (the observable A), the energy E (from the Hamiltonian H) gives:

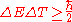
where

is the uncertainty in energy

is the uncertainty in time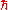

is Planck's constant

The more precisely

Accuracy and precision

In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...

one measures the duration of a sequence of events

Phenomenon

A phenomenon , plural phenomena, is any observable occurrence. Phenomena are often, but not always, understood as 'appearances' or 'experiences'...

the less precisely one can measure the energy associated with that sequence and vice versa. This equation is different from the standard uncertainty principle because time is not an operator

Operator (physics)

in quantum mechanics.

Corresponding commutator

Commutator

relations also hold for momentum p and position q, which are conjugate variables

Conjugate variables

Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals of one-another, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty in physics called the Heisenberg uncertainty...

of each other, along with a corresponding uncertainty principle in momentum and position, similar to the energy and time relation above.

Quantum mechanics explains the properties of the periodic table

Periodic table

The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...

of the elements

Chemical element

A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...

. Starting with Otto Stern

Otto Stern

Otto Stern was a German physicist and Nobel laureate in physics.-Biography:Stern was born in Sohrau, now Żory in the German Empire's Kingdom of Prussia and studied at Breslau, now Wrocław in Lower Silesia....

's and Walter Gerlach

Walter Gerlach

Walter Gerlach was a German physicist who co-discovered spin quantization in a magnetic field, the Stern-Gerlach effect.-Education:Gerlach was born in Biebrich, Hessen-Nassau....

's experiment with molecular beams in a magnetic field, Isidor Rabi (1898–1988), was able to modulate

Modulate

Modulate is Bob Mould's fifth solo album, released in 2002. Although a few tracks on his previous release, The Last Dog and Pony Show, had featured tape loops and samples, Mould shocked his fans with such a dramatic embrace of electronica...

the magnetic resonance

Magnetic resonance

Magnetic resonance can mean:*Nuclear magnetic resonance*Electron spin resonance*Magnetic resonance imaging *Functional magnetic resonance imaging *Muon spin spectroscopy...

of the beam. In 1945 Rabi then suggested that this technique be the basis of a clock using the resonant frequency of an atomic beam.

John Cramer

John G. Cramer

John G. Cramer is a professor of physics at the University of Washington in Seattle, the United States. When not teaching, he works with the STAR detector at the new Relativistic Heavy Ion Collider at Brookhaven National Laboratory, and the particle accelerator at CERN in Geneva, Switzerland...

is preparing an experiment to determine whether quantum entanglement

Quantum entanglement

Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...

is also nonlocal in time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

as it is in space

Space

. This can also be stated as 'sending a signal back in time'. Cramer has recently published an update indicating that the final experiment will take more time to prepare.

Dynamical systems

See dynamical systems and chaos theory, dissipative structures

One could say that time is a parameterization of a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

that allows the geometry of the system to be manifested and operated on. It has been asserted that time is an implicit consequence of chaos

Chaos theory

Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

(i.e. nonlinearity

Nonlinearity

In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...

/irreversibility

Irreversibility

In science, a process that is not reversible is called irreversible. This concept arises most frequently in thermodynamics, as applied to processes....

): the characteristic time

Characteristic time

The characteristic time is an estimate of the order of magnitude of the reaction time scale. It can loosely be defined as the inverse of the reaction rate...

, or rate of information entropy

Information entropy

In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...

production, of a system

System

System is a set of interacting or interdependent components forming an integrated whole....

. Mandelbrot

Mandelbrot

Mandelbrot, may refer to:* Benoît Mandelbrot , a mathematician associated with fractal geometry* Mandelbrot set, a fractal popularized by Benoît Mandelbrot* Mandelbrot Competition, a math competition- See also :...

introduces intrinsic time in his book Multifractals and 1/f noise.

Signalling

! electrical engineering

Electrical engineering

|-
! signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

Signalling is one application of the electromagnetic waves described above. In general, a signal is part of communication

Communication

Communication is the activity of conveying meaningful information. Communication requires a sender, a message, and an intended recipient, although the receiver need not be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast...

between parties and places. One example might be a yellow ribbon

Yellow ribbon

The yellow ribbon is used for various symbolic purposes. It is often worn on one's person or tied around a tree in one's front yard.- Earliest Evidence unearthed at Pompeii :...

tied to a tree, or the ringing of a church bell

Church bell

A church bell is a bell which is rung in a church either to signify the hour or the time for worshippers to go to church, perhaps to attend a wedding, funeral, or other service...

. A signal can be part of a conversation

Conversation

Conversation is a form of interactive, spontaneous communication between two or more people who are following rules of etiquette.Conversation analysis is a branch of sociology which studies the structure and organization of human interaction, with a more specific focus on conversational...

, which involves a protocol

Communications protocol

A communications protocol is a system of digital message formats and rules for exchanging those messages in or between computing systems and in telecommunications...

. Another signal might be the position of the hour hand on a town clock or a railway station. An interested party might wish to view that clock, to learn the time. See: Time ball

Time ball

A time ball is a large painted wooden or metal ball that drops at a predetermined time, principally to enable sailors to check their marine chronometers from their boats offshore...

, an early form of Time signal

Time signal

A time signal is a visible, audible, mechanical, or electronic signal used as a reference to determine the time of day.-Audible and visible time signals:...

We as observers can still signal different parties and places as long as we live within their past light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

. But we cannot receive signals from those parties and places outside our past light cone.

Along with the formulation of the equations for the electromagnetic wave, the field of telecommunication

Telecommunication

Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...

could be founded.
In 19th century telegraphy

Telegraphy

Telegraphy is the long-distance transmission of messages via some form of signalling technology. Telegraphy requires messages to be converted to a code which is known to both sender and receiver...

, electrical circuits, some spanning continent

Continent

A continent is one of several very large landmasses on Earth. They are generally identified by convention rather than any strict criteria, with seven regions commonly regarded as continents—they are : Asia, Africa, North America, South America, Antarctica, Europe, and Australia.Plate tectonics is...

s and ocean

Ocean

An ocean is a major body of saline water, and a principal component of the hydrosphere. Approximately 71% of the Earth's surface is covered by ocean, a continuous body of water that is customarily divided into several principal oceans and smaller seas.More than half of this area is over 3,000...

s, could transmit code

Code

A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....

s - simple dots, dashes and spaces. From this, a series of technical issues have emerged; see :Category:Synchronization. But it is safe to say that our signalling systems can be only approximately synchronized

Synchronization

Synchronization is timekeeping which requires the coordination of events to operate a system in unison. The familiar conductor of an orchestra serves to keep the orchestra in time....

, a plesiochronous

Plesiochronous

The term Plesiochronous is derived from the Greek plesio, meaning near, and chronos, time, and refers to the fact that plesiochronous systems run in a state where different parts of the system are almost, but not quite perfectly, synchronised....

condition, from which jitter

Jitter

Jitter is the undesired deviation from true periodicity of an assumed periodic signal in electronics and telecommunications, often in relation to a reference clock source. Jitter may be observed in characteristics such as the frequency of successive pulses, the signal amplitude, or phase of...

need be eliminated.

That said, system

System

System is a set of interacting or interdependent components forming an integrated whole....

s can be synchronized (at an engineering approximation), using technologies like GPS. The GPS satellites must account for the effects of gravitation and other relativistic factors in their circuitry. See: Self-clocking signal

Self-clocking signal

In telecommunications and electronics, a self-clocking signal is one that can be decoded without the need for a separate clock signal or other source of synchronization...

Technology for timekeeping standards

The primary time standard

Primary time standard

In telecommunications, a primary time standard is a time standard that does not require calibration against another time standard.Examples of primary time, are caesium standards and hydrogen masers....

in the U.S. is currently NIST-F1

NIST-F1

NIST-F1 is a cesium fountain clock or atomic clock in the National Institute of Standards and Technology in Boulder, Colorado, and serves as the United States' primary time and frequency standard...

, a laser

Laser

A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...

-cooled Cs

Caesium

fountain, the latest in a series of time and frequency standards, from the ammonia

Ammonia

Ammonia is a compound of nitrogen and hydrogen with the formula . It is a colourless gas with a characteristic pungent odour. Ammonia contributes significantly to the nutritional needs of terrestrial organisms by serving as a precursor to food and fertilizers. Ammonia, either directly or...

-based atomic clock (1949) to the caesium

Caesium

-based NBS-1 (1952) to NIST-7 (1993). The respective clock uncertainty declined from 10,000 nanoseconds per day to 0.5 nanoseconds per day in 5 decades. In 2001 the clock uncertainty for NIST-F1 was 0.1 nanoseconds/day. Development of increasingly accurate frequency standards is underway.

In this time and frequency standard, a population of caesium atoms is laser-cooled to temperatures of one microkelvin. The atoms collect in a ball shaped by six lasers, two for each spatial dimension, vertical (up/down), horizontal (left/right), and back/forth. The vertical lasers push the caesium ball through a microwave cavity. As the ball is cooled, the caesium population cools to its ground state and emits light at its natural frequency, stated in the definition of second above. Eleven physical effects are accounted for in the emissions from the caesium population, which are then controlled for in the NIST-F1 clock. These results are reported to BIPM.

Additionally, a reference hydrogen maser is also reported to BIPM as a frequency standard for TAI

TAI

Three letter acronym TAI may refer to:* IATA airport code for Ta'izz International Airport* ICAO code for TACA International Airlines* Transports Aériens Intercontinentaux, a now defunct French airline...

(international atomic time

International Atomic Time

International Atomic Time is a high-precision atomic coordinate time standard based on the notional passage of proper time on Earth's geoid...

).

The measurement of time is overseen by BIPM (Bureau International des Poids et Mesures), located in Sèvres

Sèvres

Sèvres is a commune in the southwestern suburbs of Paris, France. It is located from the centre of Paris.The town is known for its porcelain manufacture, the Manufacture nationale de Sèvres, making the famous Sèvres porcelain, as well as being the location of the International Bureau of Weights...

, France, which ensures uniformity of measurements and their traceability to the International System of Units

International System of Units

(SI

Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...

) worldwide. BIPM operates under authority of the Metre Convention, a diplomatic treaty between fifty-one nations, the Member States of the Convention, through a series of Consultative Committees, whose members are the respective national metrology laboratories.

Time in cosmology

The equations of general relativity predict a non-static universe. However, Einstein accepted only a static universe, and modified the Einstein field equation to reflect this by adding the cosmological constant

Cosmological constant

In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...

, which he later described as the biggest mistake of his life. But in 1927, Georges LeMaître

Georges Lemaître

Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...

(1894–1966) argued, on the basis of general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, that the universe originated in a primordial explosion. At the fifth Solvay conference

Solvay Conference

The International Solvay Institutes for Physics and Chemistry, located in Brussels, were founded by the Belgian industrialist Ernest Solvay in 1912, following the historic invitation-only 1911 Conseil Solvay, the turning point in world physics...

, that year, Einstein brushed him off with "" (“Your math is correct, but your physics is abominable”). In 1929, Edwin Hubble

Edwin Hubble

Edwin Powell Hubble was an American astronomer who profoundly changed the understanding of the universe by confirming the existence of galaxies other than the Milky Way - our own galaxy...

(1889–1953) announced his discovery of the expanding universe. The current generally accepted cosmological model, the Lambda-CDM model

Lambda-CDM model

ΛCDM or Lambda-CDM is an abbreviation for Lambda-Cold Dark Matter, which is also known as the cold dark matter model with dark energy...

, has a positive cosmological constant and thus not only an expanding universe but an accelerating expanding universe.

If the universe were expanding, then it must have been much smaller and therefore hotter and denser in the past. George Gamow

George Gamow

George Gamow , born Georgiy Antonovich Gamov , was a Russian-born theoretical physicist and cosmologist. He discovered alpha decay via quantum tunneling and worked on radioactive decay of the atomic nucleus, star formation, stellar nucleosynthesis, Big Bang nucleosynthesis, cosmic microwave...

(1904–1968) hypothesized that the abundance of the elements in the Periodic Table of the Elements, might be accounted for by nuclear reactions in a hot dense universe. He was disputed by Fred Hoyle

Fred Hoyle

Sir Fred Hoyle FRS was an English astronomer and mathematician noted primarily for his contribution to the theory of stellar nucleosynthesis and his often controversial stance on other cosmological and scientific matters—in particular his rejection of the "Big Bang" theory, a term originally...

(1915–2001), who invented the term 'Big Bang

Big Bang

' to disparage it. Fermi

Enrico Fermi

Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...

and others noted that this process would have stopped after only the light elements were created, and thus did not account for the abundance of heavier elements.

Gamow's prediction was a 5–10 kelvin

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

black body radiation temperature for the universe, after it cooled during the expansion. This was corroborated by Penzias and Wilson in 1965. Subsequent experiments arrived at a 2.7 kelvin temperature, corresponding to an age of the universe

Age of the universe

The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...

of 13.7 billion years after the Big Bang.

This dramatic result has raised issues: what happened between the singularity of the Big Bang and the Planck time, which, after all, is the smallest observable time. When might have time separated out from the spacetime foam; there are only hints based on broken symmetries (see Spontaneous symmetry breaking

Spontaneous symmetry breaking

Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....

, Timeline of the Big Bang

Timeline of the Big Bang

This timeline of the Big Bang describes the history of the universe according to the prevailing scientific theory of how the universe came into being, using the cosmological time parameter of comoving coordinates...

, and the articles in :Category:Physical cosmology).

General relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

gave us our modern notion of the expanding universe that started in the Big Bang. Using relativity and quantum theory we have been able to roughly reconstruct the history of the universe. In our epoch

Age of the universe

, during which electromagnetic waves can propagate without being disturbed by conductors or charges, we can see the stars, at great distances from us, in the night sky. (Before this epoch, there was a time, 300,000 years after the big bang

Big Bang

, during which starlight would not have been visible.)

Reprise

Ilya Prigogine

Ilya, Viscount Prigogine was a Russian-born naturalized Belgian physical chemist and Nobel Laureate noted for his work on dissipative structures, complex systems, and irreversibility.-Biography :...

's reprise is "Time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

precedes existence

Existence

In common usage, existence is the world we are aware of through our senses, and that persists independently without them. In academic philosophy the word has a more specialized meaning, being contrasted with essence, which specifies different forms of existence as well as different identity...

". He contrasts the views of Newton, Einstein and quantum physics which offer a symmetric view of time (as discussed above) with his own views, which point out that statistical and thermodynamic physics can explain irreversible phenomena

Irreversibility

In science, a process that is not reversible is called irreversible. This concept arises most frequently in thermodynamics, as applied to processes....

as well as the arrow of time

Arrow of time

The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...

and the Big Bang

Big Bang

Markers of time

The unit of measurement of time: the second

The state of the art in timekeeping

Conceptions of time

Regularities in nature

Mechanical clocks

Galileo: the flow of time

Newton's physics: linear time

Thermodynamics and the paradox of irreversibility

Electromagnetism and the speed of light

Einstein's physics: spacetime

Time in quantum mechanics

Dynamical systems

Signalling

Technology for timekeeping standards

Time in cosmology

Reprise

Further reading