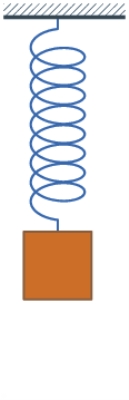
Harmonic oscillator - AbsoluteAstronomy.com

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force

Restoring force

Restoring force, in a physics context, is a variable force that gives rise to an equilibrium in a physical system. If the system is perturbed away from the equilibrium, the restoring force will tend to bring the system back toward equilibrium....

, F, proportional

Proportionality (mathematics)

In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...

to the displacement, x:

where k is a positive constant

Coefficient

In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

.

If F is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion

Simple harmonic motion

Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....

: sinusoidal oscillation

Oscillation

Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...

s about the equilibrium point, with a constant amplitude

Amplitude

Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...

and a constant frequency

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

(which does not depend on the amplitude).

If a frictional force (damping

Damping

In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...

) proportional to the velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can:

Oscillate with a frequency smaller than in the non-damped case, and an amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...

decreasing with time (underdamped oscillator).
Decay exponentially to the equilibrium position, without oscillations (overdamped oscillator).

If an external time dependent force is present, the harmonic oscillator is described as a driven oscillator.

Mechanical examples include pendula

Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...

(with small angles of displacement), masses connected to spring

Spring (device)

A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...

s, and acoustical system

Acoustics

Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...

s. Other analogous systems include electrical harmonic oscillators such as RLC circuit

RLC circuit

An RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The RLC part of the name is due to those letters being the usual electrical symbols for resistance, inductance and capacitance respectively...

s. The harmonic oscillator model is very important in physics, because any mass subject to a force in stable equilibrium acts as a harmonic oscillator for small vibrations. Harmonic oscillators occur widely in nature and are exploited in many manmade devices, such as clocks

Clock

A clock is an instrument used to indicate, keep, and co-ordinate time. The word clock is derived ultimately from the Celtic words clagan and clocca meaning "bell". A silent instrument missing such a mechanism has traditionally been known as a timepiece...

and radio circuits. They are the source of virtually all sinusoidal vibrations and waves.

Simple harmonic oscillator

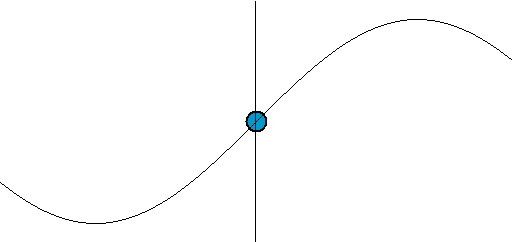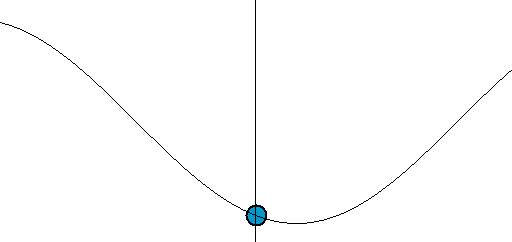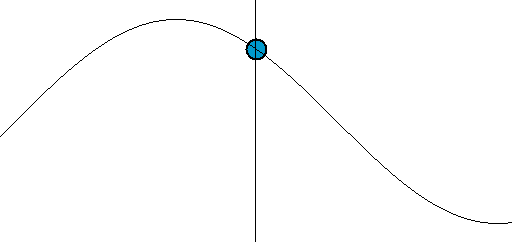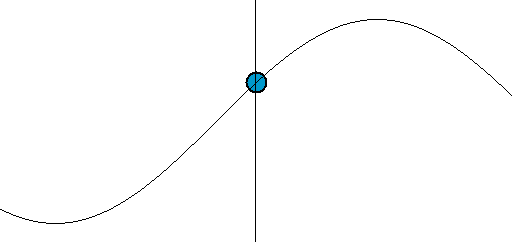
A simple harmonic oscillator is an oscillator that is neither driven nor damped

Damping

. It consists of a mass m,which experiences a single force, F, which pulls the mass in the direction of the point x=0 and depends only on the mass's position x and a constant k. Newton's second law for the system is

Solving this differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

, we find that the motion is described by the function

where

The motion is periodic

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

— repeating itself in a sinusoidal

Sine wave

The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...

fashion with constant amplitude, A. In addition to its amplitude, the motion of a simple harmonic oscillator is characterized by its period

Frequency

T, the time for a single oscillation or its frequency f = , the number of cycles per unit time. The position at a given time t also depends on the phase

Phase (waves)

Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...

, φ, which determines the starting point on the sine wave. The period and frequency are determined by the size of the mass m and the force constant k, while the amplitude and phase are determined by the starting position and velocity

Velocity

.

The velocity and acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

of a simple harmonic oscillator oscillate with the same frequency as the position but with shifted phases. The velocity is maximum for zero displacement, while the acceleration is in the opposite direction as the displacement.

The potential energy stored in a simple harmonic oscillator at position x is

Damped harmonic oscillator

In real oscillators, friction, or damping, slows the motion of the system. In many vibrating systems the frictional force F_f can be modeled as being proportional to the velocity v of the object: , where c is called the viscous damping coefficient.

Newton's second law for damped harmonic oscillators is then

This is rewritten into the form

where

is called the 'undamped angular frequency

Angular frequency

In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...

of the oscillator' and

is called the 'damping ratio'.

The value of the damping ratio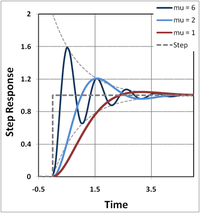 ζ critically determines the behavior of the system. A damped harmonic oscillator can be:

Overdamped (ζ > 1): The system returns (exponentially decays) to equilibrium without oscillating. Larger values of the damping ratio ζ return to equilibrium slower.
Critically damped (ζ = 1): The system returns to equilibrium as quickly as possible without oscillating. This is often desired for the damping of systems such as doors.
Underdamped (ζ < 1): The system oscillates (with a slightly different frequency than the undamped case) with the amplitude gradually decreasing to zero. The angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...

of the underdamped harmonic oscillator is given by

The Q factor

Q factor

In physics and engineering the quality factor or Q factor is a dimensionless parameter that describes how under-damped an oscillator or resonator is, or equivalently, characterizes a resonator's bandwidth relative to its center frequency....

of a damped oscillator is defined as

Q is related to the damping ratio by the equation

Driven harmonic oscillators

Driven harmonic oscillators are damped oscillators further affected by an externally applied force F(t).

Newton's second law takes the form

It is usually rewritten into the form

This equation can be solved exactly for any driving force using the solutions z(t) to the unforced equation, which satisfy

and which can be expressed as damped sinusoidal oscillations,

in the case where ζ ≤ 1. The amplitude A and phase φ determine the behavior needed to match the initial conditions.

Step input

In the case ζ < 1 and a unit step input with x(0) = 0:

the solution is:

with phase φ given by

This behavior is found in (for example) feedback amplifiers

Step response

The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...

, where the amplifier design is adjusted to obtain the fastest step response possible without undue overshoot or undershoot and with an adequate settling time.

The time an oscillator needs to adapt to changed external conditions is of the order τ = 1/(ζω₀). In physics, the adaptation is called relaxation, and τ is called the relaxation time.

In electrical engineering, a multiple of τ is called the settling time, i.e. the time necessary to insure the signal is within a fixed departure from final value, typically within 10%. The term overshoot refers to the extent the maximum response exceeds final value, and undershoot refers to the extent the response falls below final value for times following the maximum response.

Sinusoidal driving force

In the case of a sinusoidal driving force:

where

is the driving amplitude and

is the driving frequency

Frequency

for a sinusoidal driving mechanism. This type of system appears in AC

Alternating current

In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....

driven RLC circuit

RLC circuit

s (resistor

Electrical resistance

The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...

-inductor

Inductor

An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...

-capacitor

Capacitor

A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...

) and driven spring systems having internal mechanical resistance or external air resistance.

The general solution is a sum of a transient

Transient (oscillation)

A transient event is a short-lived burst of energy in a system caused by a sudden change of state.The source of the transient energy may be an internal event or a nearby event...

solution that depends on initial conditions, and a steady state

Steady state

A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...

that is independent of initial conditions and depends only on the driving amplitude

, driving frequency,

, undamped angular frequency

, and the damping ratio

.

The steady-state solution is proportional to the driving force with an induced phase change of

where

is the absolute value of the impedance

Mechanical impedance

Mechanical impedance is a measure of how much a structure resists motion when subjected to a given force. It relates forces with velocities acting on a mechanical system. The mechanical impedance of a point on a structure is the ratio of the force applied at a point to the resulting velocity at...

or linear response function

Linear response function

A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...

and

is the phase

Phase (waves)

Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...

of the oscillation relative to the driving force.

For a particular driving frequency called the resonance

Resonance

In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...

frequency

, the amplitude (for a given

) is maximum. This resonance effect only occurs when

, i.e. for significantly underdamped systems. For strongly underdamped systems the value of the amplitude can become quite large near the resonance frequency.

The transient solutions are the same as the unforced (

) damped harmonic oscillator

Damping

and represent the systems response to other events that occurred previously. The transient solutions typically die out rapidly enough that they can be ignored.

Parametric oscillators

A parametric oscillator

Parametric oscillator

A parametric oscillator is a harmonic oscillator whose parameters oscillate in time. For example, a well known parametric oscillator is a child pumping a swing by periodically standing and squatting to increase the size of the swing's oscillations. The varying of the parameters drives the system...

is a harmonic oscillator whose parameters oscillate in time.
A familiar example of both parametric and driven oscillation is playing on a swing. Rocking back and forth pumps the swing as a driven harmonic oscillator, but once moving, the swing can also be parametrically driven by alternately standing and squatting at key points in the swing. The varying of the parameters drives the system. Examples of parameters that may be varied are its resonance frequency

and damping

.

Parametric oscillators are used in many applications. The classical varactor parametric oscillator oscillates when the diode's capacitance is varied periodically. The circuit that varies the diode's capacitance is called the "pump" or "driver". In microwave electronics, waveguide

Waveguide (electromagnetism)

In electromagnetics and communications engineering, the term waveguide may refer to any linear structure that conveys electromagnetic waves between its endpoints. However, the original and most common meaning is a hollow metal pipe used to carry radio waves...

/YAG based parametric oscillators operate in the same fashion. The designer varies a parameter periodically to induce oscillations.

Parametric oscillators have been developed as low-noise amplifiers, especially in the radio and microwave frequency range. Thermal noise is minimal, since a reactance (not a resistance) is varied. Another common use is frequency conversion, e.g., conversion from audio to radio frequencies. For example, the Optical parametric oscillator

Optical parametric oscillator

An optical parametric oscillator is a parametric oscillator which oscillates at optical frequencies. It converts an input laser wave into two output waves of lower frequency by means of second order nonlinear optical interaction. The sum of the output waves frequencies is equal to the input wave...

converts an input laser

Laser

A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...

wave into two output waves of lower frequency (

).

Parametric resonance occurs in a mechanical system when a system is parametrically excited and oscillates at one of its resonant frequencies. Parametric excitation differs from forcing, since the action appears as a time varying modification on a system parameter. This effect is different from regular resonance because it exhibits the instability

Instability

In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...

phenomenon.

Universal oscillator equation

The equation

is known as the universal oscillator equation since all second order linear oscillatory systems can be reduced to this form. This is done through nondimensionalization

Nondimensionalization

Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...

.

If the forcing function is f(t) = cos(ωt) = cos(ωt_cτ) = cos(ωτ), where ω = ωt_c, the equation becomes

The solution to this differential equation contains two parts, the "transient" and the "steady state".

Transient solution

The solution based on solving the ordinary differential equation

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

is for arbitrary constants c₁ and c₂

The transient solution is independent of the forcing function.

Steady-state solution

Apply the "complex variables

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

method" by solving the auxiliary equation below and then finding the real part of its solution:

Supposing the solution is of the form

Its derivatives from zero to 2nd order are

Substituting these quantities into the differential equation gives

Dividing by the exponential term on the left results in

Equating the real and imaginary parts results in two independent equations

Amplitude part

Squaring both equations and adding them together gives

By convention the positive root is taken since amplitude is usually considered a positive quantity. Therefore,

Compare this result with the theory section on resonance

Resonance

In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...

, as well as the "magnitude part" of the RLC circuit

RLC circuit

. This amplitude function is particularly important in the analysis and understanding of the frequency response

Frequency response

Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...

of second-order systems.

Phase part

To solve for φ, divide both equations to get

This phase function is particularly important in the analysis and understanding of the frequency response

Frequency response

of second-order systems.

Full solution

Combining the amplitude and phase portions results in the steady-state solution

The solution of original universal oscillator equation is a superposition

Superposition principle

In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...

(sum) of the transient and steady-state solutions

For a more complete description of how to solve the above equation, see linear ODEs with constant coefficients.

Equivalent systems

Harmonic oscillators occurring in a number of areas of engineering are equivalent in the sense that their mathematical models are identical (see universal oscillator equation above). Below is a table showing analogous quantities in four harmonic oscillator systems in mechanics and electronics. If analogous parameters on the same line in the table are given numerically equal values, the behavior of the oscillators—their output waveform, resonant frequency, damping factor, etc.—are the same.

Translational Mechanical	Torsional Mechanical	Series RLC Circuit	Parallel RLC Circuit
Position	Angle	Charge Charge (physics) In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...	Voltage Voltage Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
Velocity Velocity In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...	Angular velocity Angular velocity In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...	Current Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
Mass Mass Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...	Moment of inertia Moment of inertia In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...	Inductance Inductance In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit...	Capacitance Capacitance In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
Spring constant Hooke's law In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...	Torsion constant	Elastance	Susceptance Susceptance In electrical engineering, susceptance is the imaginary part of admittance. The inverse of admittance is impedance and the real part of admittance is conductance. In SI units, susceptance is measured in siemens...
Friction Friction Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...	Rotational friction	Resistance Electrical resistance The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...	Conductance
Drive force Force In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...	Drive torque Torque Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
Undamped resonant frequency Resonance In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies... :

Differential equation:

Application to a conservative force

The problem of the simple harmonic oscillator occurs frequently in physics, because a mass at equilibrium under the influence of any conservative force

Conservative force

A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...

, in the limit of small motions, behaves as a simple harmonic oscillator.

A conservative force is one that has a potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

function. The potential energy function of a harmonic oscillator is:

Given an arbitrary potential energy function

, one can do a Taylor expansion

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

in terms of

around an energy minimum (

) to model the behavior of small perturbations from equilibrium.

Because

is a minimum, the first derivative evaluated at

must be zero, so the linear term drops out:

The constant term

Constant term

In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....

V(x₀) is arbitrary and thus may be dropped, and a coordinate transformation allows the form of the simple harmonic oscillator to be retrieved:

Thus, given an arbitrary potential energy function

with a non-vanishing second derivative, one can use the solution to the simple harmonic oscillator to provide an approximate solution for small perturbations around the equilibrium point.

Simple pendulum

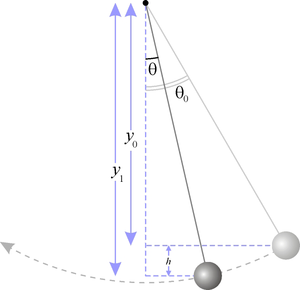
Assuming no damping and small amplitudes, the differential equation governing a simple pendulum is

The solution to this equation is given by:

where

is the largest angle attained by the pendulum. The period

Sine

In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....

, the time for one complete oscillation, is given by

divided by whatever is multiplying the time in the argument of the cosine (

here).

Pendulum swinging over turntable

Simple harmonic motion can in some cases be considered to be the one-dimensional projection

Projection (mathematics)

Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...

of two-dimensional circular motion

Circular motion

In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...

. Consider a long pendulum

Pendulum

swinging over the turntable of a record player. On the edge of the turntable there is an object. If the object is viewed from the same level as the turntable, a projection of the motion of the object seems to be moving backwards and forwards on a straight line orthogonal to the view direction, sinusoidally like the pendulum.

Spring–mass system

When a spring is stretched or compressed by a mass, the spring develops a restoring force. Hooke's law

Hooke's law

In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...

gives the relationship of the force exerted by the spring when the spring is compressed or stretched a certain length:

where F is the force, k is the spring constant, and x is the displacement of the mass with respect to the equilibrium position. This relationship shows that the distance of the spring is always opposite to the force of the spring.

By using either force balance or an energy method, it can be readily shown that the motion of this system is given by the following differential equation:

...the latter evidently being Newton's second law of motion.

If the initial displacement is A, and there is no initial velocity, the solution of this equation is given by:

Given an ideal massless spring,

is the mass on the end of the spring. If the spring itself has mass, its effective mass

Effective mass (spring-mass system)

In a spring-mass system the mass of the spring m, as well as the suspended mass M, have an influence on the motion. However, since not all of the spring moves at the same velocity as the suspended mass, the mass of the spring cannot be simply added to the suspended mass...

must be included in

Energy variation in the spring–damping system

In terms of energy, all systems have two types of energy, potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

and kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

. When a spring is stretched or compressed, it stores elastic potential energy, which then is transferred into kinetic energy. The potential energy within a spring is determined by the equation

When the spring is stretched or compressed, kinetic energy of the mass gets converted into potential energy of the spring. By conservation of energy, assuming the datum is defined at the equilibrium position, when the spring reaches its maximum potential energy, the kinetic energy of the mass is zero. When the spring is released, it tries to return to equilibrium, and all its potential energy converts to kinetic energy of the mass.

External links

Harmonic Oscillator from The Chaos Hypertextbook
A Java applet of harmonic oscillator with damping proportional to velocity or damping caused by dry friction

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Simple harmonic oscillator

Damped harmonic oscillator

Driven harmonic oscillators

Step input

Sinusoidal driving force

Parametric oscillators

Universal oscillator equation

Transient solution

Steady-state solution

Amplitude part

Phase part

Full solution

Equivalent systems

Application to a conservative force

Simple pendulum

Pendulum swinging over turntable

Spring–mass system

Energy variation in the spring–damping system

See also

External links