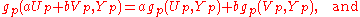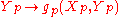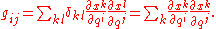Metric tensor
Encyclopedia
In the mathematical
field of differential geometry, a metric tensor is a type of function defined on a manifold
(such as a surface
in space) which takes as input a pair of tangent vector
s v and w and produces a real number
(scalar
) g(v,w) in a way that generalizes many of the familiar properties of the dot product
of vectors in Euclidean space
. In the same way as a dot product, metric tensors are used to define the length of, and angle between, tangent vectors.
A manifold equipped with a metric tensor is known as a Riemannian manifold
. By integration
, the metric tensor allows one to define and compute the length of curves on the manifold. The curve connecting two points that has the smallest length is called a geodesic
, and its length is the distance that a passenger in the manifold needs to traverse to go from one point to the other. Equipped with this notion of length, a Riemannian manifold is a metric space
, meaning that it has a distance function
d(p,q) whose value at a pair of points p and q is the distance from p to q. Conversely, the metric tensor itself is the derivative
of the distance function (taken in a suitable manner). Thus the metric tensor gives the infinitesimal distance on the manifold.
While the notion of a metric tensor was known in some sense to mathematicians such as Carl Gauss from the early 19th century, it was not until the early 20th century that its properties as a tensor
were understood by, in particular, Gregorio Ricci-Curbastro
and Tullio Levi-Civita
who first codified the notion of a tensor. The metric tensor is an example of a tensor field
, meaning that relative to a local coordinate system on the manifold, a metric tensor takes on the form of a symmetric matrix whose entries transform covariantly under changes to the coordinate system. Thus a metric tensor is a covariant symmetric tensor. From the coordinate-independent point of view, a metric tensor is defined to be a nondegenerate symmetric bilinear form
on each tangent space that varies smoothly
from point to point.
in his 1827 Disquisitiones generales circa superficies curvas (General investigations of curved surfaces) considered a surface parametrically
, with the Cartesian coordinates x, y, and z of points on the surface depending on two auxiliary variables u and v. Thus a parametric surface is (in today's terms) a vector valued function
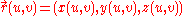
depending on an ordered pair
of real variables (u,v), and defined in an open set
D in the uv-plane. One of the chief aims of Gauss' investigations was to deduce those features of the surface which could be described by a function which would remain unchanged if the surface underwent a transformation in space (such as bending the surface without stretching it), or a change in the particular parametric form of the same geometrical surface.
One natural such invariant quantity is the length of a curve drawn along the surface. Another is the angle
between a pair of curves drawn along the surface and meeting at a common point, or tangent vector
s at the same point of the surface. A third such quantity is the area
of a piece of the surface. The study of these invariants of a surface led Gauss to introduce the predecessor of the modern notion of the metric tensor.
[a,b], then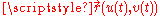 will trace out a parametric curve in M. The arclength of that curve is given by the integral
will trace out a parametric curve in M. The arclength of that curve is given by the integral
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry, a metric tensor is a type of function defined on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(such as a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
in space) which takes as input a pair of tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s v and w and produces a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
) g(v,w) in a way that generalizes many of the familiar properties of the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of vectors in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In the same way as a dot product, metric tensors are used to define the length of, and angle between, tangent vectors.
A manifold equipped with a metric tensor is known as a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. By integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, the metric tensor allows one to define and compute the length of curves on the manifold. The curve connecting two points that has the smallest length is called a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
, and its length is the distance that a passenger in the manifold needs to traverse to go from one point to the other. Equipped with this notion of length, a Riemannian manifold is a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, meaning that it has a distance function
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d(p,q) whose value at a pair of points p and q is the distance from p to q. Conversely, the metric tensor itself is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the distance function (taken in a suitable manner). Thus the metric tensor gives the infinitesimal distance on the manifold.
While the notion of a metric tensor was known in some sense to mathematicians such as Carl Gauss from the early 19th century, it was not until the early 20th century that its properties as a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
were understood by, in particular, Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
and Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
who first codified the notion of a tensor. The metric tensor is an example of a tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
, meaning that relative to a local coordinate system on the manifold, a metric tensor takes on the form of a symmetric matrix whose entries transform covariantly under changes to the coordinate system. Thus a metric tensor is a covariant symmetric tensor. From the coordinate-independent point of view, a metric tensor is defined to be a nondegenerate symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
on each tangent space that varies smoothly
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
from point to point.
Introduction
Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in his 1827 Disquisitiones generales circa superficies curvas (General investigations of curved surfaces) considered a surface parametrically
Parametric surface
A parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
, with the Cartesian coordinates x, y, and z of points on the surface depending on two auxiliary variables u and v. Thus a parametric surface is (in today's terms) a vector valued function
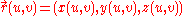
depending on an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of real variables (u,v), and defined in an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
D in the uv-plane. One of the chief aims of Gauss' investigations was to deduce those features of the surface which could be described by a function which would remain unchanged if the surface underwent a transformation in space (such as bending the surface without stretching it), or a change in the particular parametric form of the same geometrical surface.
One natural such invariant quantity is the length of a curve drawn along the surface. Another is the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
between a pair of curves drawn along the surface and meeting at a common point, or tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s at the same point of the surface. A third such quantity is the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of a piece of the surface. The study of these invariants of a surface led Gauss to introduce the predecessor of the modern notion of the metric tensor.
Arclength
If the variables u and v are taken to depend on a third variable, t, taking values in an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a,b], then
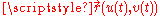 will trace out a parametric curve in M. The arclength of that curve is given by the integral
will trace out a parametric curve in M. The arclength of that curve is given by the integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
-
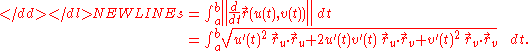
where represents the Euclidean norm. Here the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
represents the Euclidean norm. Here the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
has been applied, and the subscripts denote partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s. The integrand is the restriction to the curve of the square root of the (quadraticQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
) differentialDifferential (mathematics)In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
where
The quantity ds in is called the line elementLine elementA line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
, while ds2 is called the first fundamental formFirst fundamental formIn differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
of M. Intuitively, it represents the principal partPrincipal partIn mathematics, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series of a function.-Laurent series definition:...
of the square of the displacement undergone by when u is increased by du units, and v is increased by dv units.
when u is increased by du units, and v is increased by dv units.
Using matrix notation, the first fundamental form becomes
Coordinate transformations
Suppose now that a different parameterization is selected, by allowing u and v to depend on another pair of variables u′ and v′. Then the analog of for the new variables is
The chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
relates E′, F′, and G′ to E,F, and G via the matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
equation
where the superscript T denotes the matrix transpose. The matrix with the coefficients E, F, and G arranged in this way therefore transforms by the Jacobian matrix of the coordinate change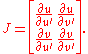
A matrix which transforms in this way is one kind of what is called a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. The matrix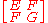
with the transformation law is known as the metric tensor of the surface.
Invariance of arclength under coordinate transformations
first observed the significance of a system of coefficients E, F, and G, that transformed in this way on passing from one system of coordinates to another. The upshot is that the first fundamental form is invariant under changes in the coordinate system, and that this follows exclusively from the transformation properties of E, F, and G. Indeed, by the chain rule,
so that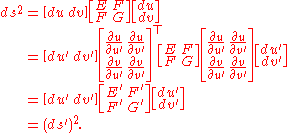
Inner product of two tangent vectors
Another interpretation of the metric tensor, also considered by Gauss, is that it provides a way in which to compute the angle between two tangent vectorTangent vectorA tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s to the surface. In contemporary terms, the metric tensor allows one to compute the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of tangent vectors in a manner independent of the parametric description of the surface. Any tangent vector at a point of the parametric surface M can be written in the form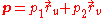
for suitable real numbers p1 and p2. If two tangent vectors are given

then using the bilinearBilinearBilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
ity of the dot product,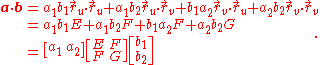
This is plainly a function of the four variables a1, b1, a2, and b2. It is more profitably viewed, however, as a function that takes a pair of arguments a = [a1 a2] and b = [b1 b2] which are vectors in the uv-plane. That is, put
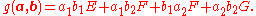
This is a symmetric functionSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
in a and b, meaning that
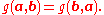
It is also bilinear meaning that it is linearLinear functionalIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
in each variable a and b separately. That is,
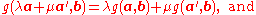

for any vectors a, a′, b, and b′ in the uv plane, and any real numbers μ and λ.
Euclidean norm of a tangent vector
The Euclidean norm of a tangent vector a is simply the square root of the inner product of the vector with itself:
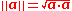
Angle between two tangent vectors
The angle θ between two tangent vectors a and b can be calculated from their inner product:

Therefore,
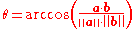
Area
The surface areaSurface areaSurface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
is another numerical quantity which should depend only on the surface itself, and not on how it is parameterized. If the surface M is parameterized by the function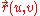 over the domain D in the uv-plane, then the surface area of M is given by the integral
over the domain D in the uv-plane, then the surface area of M is given by the integral

where × denotes the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, and the absolute value denotes the length of a vector in Euclidean space. By Lagrange's identity for the cross product, the integral can be written

where det is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
.
Definition
Let M be a smooth manifold of dimension n; for instance a surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(in the case n = 2) or hypersurfaceHypersurfaceIn geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
in the Cartesian space Rn+1. At each point p ∈ M there is a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
TpM, called the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
, consisting of all tangent vectors to the manifold at the point p. A metric at p is a function gp(Xp,Yp) which takes as inputs a pair of tangent vectors Xp and Yp at p, and produces as an output a real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
), so that the following conditions are satisfied:
- gp is bilinearBilinearBilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
. A function of two vector arguments is bilinear if it is linear separately in each argument. Thus if Up, Vp, Yp are three tangent vectors at p and a and b are real numbers, then
- gp is symmetricSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
. A function of two vector arguments is symmetric provided that for all vectors Xp and Yp,
- gp is nondegenerate. A bilinear function is nondegenerate provided that, for every tangent vector Xp ≠ 0, the function
-
- obtained by holding Xp constant and allowing Yp to vary is not identically zero. That is, for every Xp ≠ 0 there exists a Yp such that gp(Xp,Yp) ≠ 0.
A metric tensor g on M assigns to each point p of M a metric gp in the tangent space at p in a way that varies smoothlySmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
with p. More precisely, given any open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U of manifold M and any (smooth) vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s X and Y on U, the real function
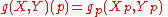
is a smooth function of p.
Components of the metric
The components of the metric in any basis of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, or frameFrame bundleIn mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
, f = (X1, …, Xn) are given by
The n2 functions gij[f] form the entries of an n×n symmetric matrix, G[f]. If
are two vectors at p ∈ U, then the value of the metric applied to v and w is determined by the coefficients by bilinearity:

Denoting the matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(gij[f]) by G[f] and arranging the components of the vectors v and w into column vectors v[f] and w[f],

where v[f]T and w[f]T denote the transpose of the vectors v[f] and w[f], respectively. Under a change of basisChange of basisIn linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
of the form
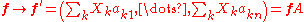
for some invertible n×n matrix A = (aij), the matrix of components of the metric changes by A as well. That is,
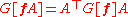
or, in terms of the entries of this matrix,

For this reason, the system of quantities gij[f] is said to transform covariantly with respect to changes in the frame f.
Metric in coordinates
A system of n real valued functions (x1, …, xn), giving a local coordinate systemLocal coordinatesLocal coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
on an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U in M, determines a basis of vector fields on U

The metric g has components relative to this frame given by
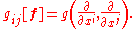
Relative to a new system of local coordinates, say
the metric tensor will determine a different matrix of coefficients,
This new system of functions is related to the original gij(f) by means of the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
so that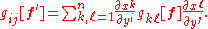
Or, in terms of the matrices G[f] = (gij[f]) and G[f′] = (gij[f′]),
where Dy denotes the Jacobian matrix of the coordinate change.
Signature of a metric
Associated to any metric tensor is the quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
defined in each tangent space by

If qm is positive for all non-zero Xm, then the metric is positive definite at m. If the metric is positive definite at every m ∈ M, then g is called a Riemannian metric. More generally, if the quadratic forms qm have constant signature independent of m, then the signature of g is this signature, and g is called a pseudo-Riemannian metric. If M is connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, then the signature of qm does not depend on m.
By Sylvester's law of inertiaSylvester's law of inertiaSylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
, a basis of tangent vectors Xi can be chosen locally so that the quadratic form diagonalizes in the following manner

for some p between 1 and n. Any two such expressions of q (at the same point m of M) will have the same number p of positive signs. The signature of g is the pair of integers (p, n − p), signifying that there are p positive signs and n − p negative signs in any such expression. Equivalently, the metric has signature (p,n − p) if the matrix gij of the metric has p positive and n − p negative eigenvalues.
Certain metric signatures which arise frequently in applications are:
- If g has signature (n, 0), then g is a Riemannian metric, and M is called a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. Otherwise, g is a pseudo-Riemannian metric, and M is called a pseudo-Riemannian manifoldPseudo-Riemannian manifoldIn differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
(the term semi-Riemannian is also used).
- If M is four-dimensional with signature (1,3) or (3,1), then the metric is called Lorentzian. More generally, a metric tensor in dimension n other than 4 of signature (1,n − 1) or (n − 1, 1) is sometimes also called Lorentzian.
- If M is 2n-dimensional and g has signature (n,n), then the metric is called ultrahyperbolic.
Inverse metric
Let f = (X1, …, Xn) be a basis of vector fields, and as above let G[f] be the matrix of coeffients
One can consider the inverse matrix G[f]−1, which is identified with the inverse metric (or conjugate or dual metric). The inverse metric satisfies a transformation law when the frame f is changed by a matrix A via
The inverse metric transforms contravariantly, or with respect to the inverse of the change of basis matrix A. Whereas the metric itself provides a way to measure the length of (or angle between) vector fields, the inverse metric supplies a means of measuring the length of (or angle between) covector fields; that is, fields of linear functionalLinear functionalIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s.
To see this, suppose that α is a covector field. To wit, for each point p, α determines a function αp defined on tangent vectors at p so that the following linearityLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
condition holds for all tangent vectors Xp and Yp, and all real numbers a and b:
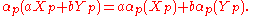
As p varies, α is assumed to be a smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
in the sense that
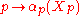
is a smooth function of p for any smooth vector field X.
Any covector field α has components in the basis of vector fields f. These are determined by

Denote the row vector of these components by
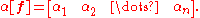
Under a change of f by a matrix A, α[f] changes by the rule

That is, the row vector of components α[f] transforms as a covariant vector.
For a pair α and β of covector fields, define the inverse metric applied to these two covectors by
The resulting definition, although it involves the choice of basis f, does not actually depend on f in an essential way. Indeed, changing basis to fA gives
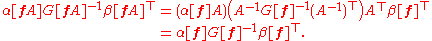
So that the right-hand side of equation is unaffected by changing the basis f to any other basis fA whatsoever. Consequently, the equation may be assigned a meaning independently of the choice of basis. The entries of the matrix G[f] are denoted by gij, where the indices i and j have been raised to indicate the transformation law .
Raising and lowering indices
In a basis of vector fields f = (X1, …, Xn), any smooth tangent vector field X can be written in the form
for some uniquely determined smooth functions v1, …, vn. Upon changing the basis f by a nonsingular matrix A, the coefficients vi change in such a way that equation remains true. That is,
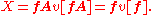
Consequently, v[fA] = A−1v[f]. In other words, the components of a vector transform contravariantly (with respect to the inverse) under a change of basis by the nonsingular matrix A. The contravariance of the components of v[f] is notationally designated by placing the indices of vi[f] in the upper position.
A frame also allows covectors to be expressed in terms of their components. For the basis of vector fields f = (X1, …, Xn) define the dual basis to be the linear functionalLinear functionalIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s (θ1[f], …, θn[f]) such that
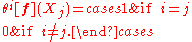
That is, θi[f](Xj) = δji, the Kronecker delta. Let
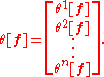
Under a change of basis f → fA for a nonsingular matrix A, θ[f] transforms via
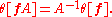
Any linear functional α on tangent vectors can be expanded in terms of the dual basis θ
where a[f] denotes the row vector [a1[f] … an[f] ]. The components ai transform when the basis f is replaced by fA in such a way that equation continues to hold. That is,

whence, because θ[fA] = A−1θ[f], it follows that a[fA] = a[f]A. That is, the components a transform covariantly (by the matrix A rather than its inverse). The covariance of the components of a[f] is notationally designated by placing the indices of ai[f] in the lower position.
Now, the metric tensor gives a means to identify vectors and covectors as follows. Holding Xp fixed, the function

of tangent vector Yp defines a linear functionalLinear functionalIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the tangent space at p. This operation takes a vector Xp at a point p and produces a covector gp(Xp, −). In a basis of vector fields f, if a vector field X has components v[f], then the components of the covector field g(X, −) in the dual basis are given by the entries of the row vector
Under a change of basis f→fA, the right-hand side of this equation transforms via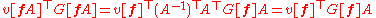
so that a[fA] = a[f]A: a transforms covariantly. The operation of associating to the (contravariant) components of a vector field v[f] = [v1[f] v2[f] … vn[f] ]T the (covariant) components of the covector field a[f] = [a1[f] a2[f] … an[f] ] where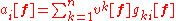
is called lowering the index.
To raise the index, one applies the same construction but with the inverse metric instead of the metric. If a[f] = [a1[f] a2[f] … an[f] ] are the components of a covector in the dual basis θ[f], then the column vector
has components which transform contravariantly: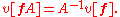
Consequently, the quantity X = fv[f] does not depend on the choice of basis f in an essential way, and thus defines a vector field on M. The operation associating to the (covariant) components of a covector a[f] the (contravariant) components of a vector v[f] given is called raising the index. In components, is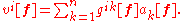
Induced metric
Let U be an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in Rn, and let φ be a continuously differentiable function from U into the Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rm where m > n. The mapping φ is called an immersion if φ is an injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and the Jacobian matrix of φ has rank n at every point of U. The image of φ is called an immersed submanifold.
Suppose that φ is an immersion onto the submanifold M ⊂ Rm. The usual Euclidean dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
in Rm is a metric which, when restricted to vectors tangent to M, gives a means for taking the dot product of these tangent vectors. This is called the induced metric.
Suppose that v is a tangent vector at a point of U, say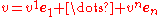
where ei are the standard coordinate vectors in Rn. When φ is applied to U, the vector v goes over to the vector tangent to M given by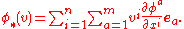
(This is called the pushforward of v along φ.) Given two such vectors, v and w, the induced metric is defined by
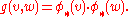
It follows from a straightforward calculation that the matrix of the induced metric in the basis of coordinate vector fields e is given by
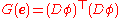
where Dφ is the Jacobian matrix:
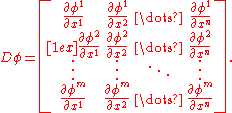
Intrinsic definitions of a metric
The notion of a metric can be defined intrinsically using the language of fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s and vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s. In these terms, a metric tensor is a function
from the fiber product of the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M to R such that the restriction of g to each fiber is a nondegenerate bilinear mapping

The mapping is required to be continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and often continuously differentiable, smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, or real analytic, depending on the case of interest, and whether M can support such a structure.
Metric as a section of a bundle
By the universal property of the tensor product, any bilinear mapping gives rise naturallyNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
to a sectionSection (fiber bundle)In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
g⊗ of the dualDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the tensor product bundle of TM with itself
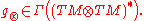
The section g⊗ is defined on simple elements of TM⊗TM by
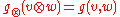
and is defined on arbitrary elements of TM⊗TM by extending linearly to linear combinations of simple elements. The original bilinear form g is symmetric if and only if
where
is the braiding map.
Since M is finite-dimensional, there is a natural isomorphism

so that g⊗ is regarded also as a section of the bundle T*M⊗T*M of the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*M with itself. Since g is symmetric as a bilinear mapping, it follows that g⊗ is a symmetric tensor.
Metric in a vector bundle
More generally, one may speak of a metric in a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
. If E is a vector bundle over a manifold M, then a metric is a mapping

from the fiber product of E to R which is bilinear in each fiber:
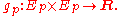
Using duality as above, a metric is often identified with a sectionSection (fiber bundle)In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
bundle , (See metric (vector bundle)Metric (vector bundle)In differential geometry, the notion of a metric tensor can be extended to an arbitrary vector bundle. Specifically, if M is a topological manifold and E → M a vector bundle on M, then a metric on E is a bundle map g : E ×M E → M × R from the fiber product of E with itself...
, (See metric (vector bundle)Metric (vector bundle)In differential geometry, the notion of a metric tensor can be extended to an arbitrary vector bundle. Specifically, if M is a topological manifold and E → M a vector bundle on M, then a metric on E is a bundle map g : E ×M E → M × R from the fiber product of E with itself...
.)
Tangent-cotangent isomorphism
The metric tensor gives a natural isomorphism from the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
to the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, sometimes called the musical isomorphismMusical isomorphismIn mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
. This isomorphism is obtained by setting, for each tangent vector Xp ∈ TpM,
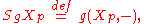
the linear functionalLinear functionalIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on TpM which sends a tangent vector Yp at p to gp(Xp,Yp). That is, in terms of the pairing [−,−] between TpM and its dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
Tp*M,
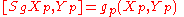
for all tangent vectors Xp and Yp. The mapping Sg is a linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
from TpM to Tp*M. It follows from the definition of non-degeneracy that the kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of Sg is reduced to zero, and so by the rank-nullity theoremRank-nullity theoremIn mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
, Sg is a linear isomorphism. Furthermore, Sg is a symmetric linear transformation in the sense that

for all tangent vectors Xp and Yp.
Conversely, any linear isomorphism S : TpM → TpM defines a non-degenerate bilinear form on TpM by means of

This bilinear form is symmetric if and only if S is symmetric. There is thus a natural one-to-one correspondence between symmetric bilinear forms on TpM and symmetric linear isomorphisms of TpM to the dual Tp*M.
As p varies over M, Sg defines a section of the bundle Hom(TM,T*M) of vector bundle isomorphisms of the tangent bundle to the cotangent bundle. This section has the same smoothness as g: it is continuous, differentiable, smooth, or real-analytic according as g. The mapping Sg, which associates to every vector field on M a covector field on M gives an abstract formulation of "lowering the index" on a vector field. The inverse of Sg is a mapping T*M → TM which, analogously, gives an abstract formulation of "raising the index" on a covector field.
The inverse Sg−1 defines a linear mapping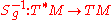
which is nonsingular and symmetric in the sense that
for all covectors α, β. Such a nonsingular symmetric mapping gives rise (by the tensor-hom adjunction) to a map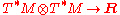
or by the double dual isomorphism to a section of the tensor product
Arclength and the line element
Suppose that g is a Riemannian metric on M. In a local coordinate system xi, i = 1,2,…,n, the metric tensor appears as a matrix, denoted here by G, whose entries are the components gij of the metric tensor relative to the coordinate vector fields.
Let γ(t) be a piecewise differentiable parametric curve in M, for a ≤t ≤ b. The arclength of the curve is defined by
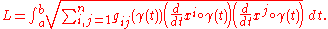
In connection with this geometrical application, the quadraticQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
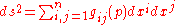
is called the first fundamental formFirst fundamental formIn differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
associated to the metric, while ds is the line elementLine elementA line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
. When ds2 is pulled back to the image of a curve in M, it represents the square of the differential with respect to arclength.
For a pseudo-Riemannian metric, the length formula above is not always defined, because the term under the square root may become negative. We generally only define the length of a curve when the quantity under the square root is always of one sign or the other. In this case, define
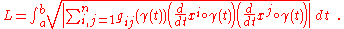
Note that, while these formulas use coordinate expressions, they are in fact independent of the coordinates chosen; they depend only on the metric, and the curve along which the formula is integrated.
The energy, variational principles and geodesics
Given a segment of a curve, another frequently defined quantity is the (kinetic) energy of the curve:
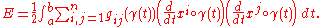
This usage comes from physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, specifically, classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, where the integral E can be seen to directly correspond to the kinetic energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of a point particle moving on the surface of a manifold. Thus, for example, in Jacobi's formulation of Maupertuis principle, the metric tensor can be seen to correspond to the mass tensor of a moving particle.
In many cases, whenever a calculation calls for the length to be used, a similar calculation using the energy may be done as well. This often leads to simpler formulas by avoiding the need for the square-root. Thus, for example, the geodesic equations may be obtained by applying variational principleVariational principleA variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
s to either the length or the energy. In the later case, the geodesic equations are seen to arise from the principle of least actionPrinciple of least actionIn physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
: they describe the motion of a "free particle" (a particle feeling no forces) that is confined to move on the manifold, but otherwise moves freely, with constant momentum, within the manifold.
Canonical measure and volume form
In analogy with the case of surfaces, a metric tensor on an n-dimensional paracompact manifold M gives rise to a natural way to measure the n-dimensional volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of subsets of the manifold. The resulting natural positive Borel measure allows one to develop a theory of integrating functions on the manifold by means of the associated Lebesgue integral.
A measure can be defined, by the Riesz representation theoremRiesz representation theoremThere are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, by giving a positive linear functionalLinear functionalIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
Λ on the space C0(M) of compactly supported continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on M. More precisely, if M is a manifold with a (pseudo-)Riemannian metric tensor g, then there is a unique positive Borel measure μg such that for any coordinate chart (U,φ),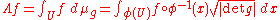
for all ƒ supported in U. Here det g is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix formed by the components of the metric tensor in the coordinate chart. That Λ is well-defined on functions supported in coordinate neighborhoods is justified by Jacobian change of variablesIntegration by substitutionIn calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
. It extends to a unique positive linear functional on C0(M) by means of a partition of unity.
If M is in addition orientedOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, then it is possible to define a natural volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
from the metric tensor. In a positively oriented coordinate system (x1,...,xn) the volume form is represented as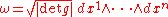
where the dxi are the coordinate differentials and the wedge ∧ denotes the exterior product in the algebra of differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. The volume form also gives a way to integrate functions on the manifold, and this geometric integral agrees with the integral obtained by the canonical Borel measure.
The Euclidean metric
The most familiar example is that of elementary Euclidean geometryEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
: the two-dimensional EuclideanEuclideanEuclidean relates to Euclid , a town or others. It may refer to:Geometry...
metric tensor. In the usual -
-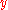 coordinates, we can write
coordinates, we can write

The length of a curve reduces to the formula:
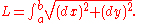
The Euclidean metric in some other common coordinate systems can be written as follows.
Polar coordinates:
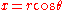

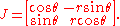
So
by trigonometric identities.
In general, in a Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
xi on a Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the partial derivatives are orthonormal with respect to the Euclidean metric. Thus the metric tensor is the Kronecker delta δij in this coordinate system. The metric tensor with respect to arbitrary (possibly curvilinear) coordinates
are orthonormal with respect to the Euclidean metric. Thus the metric tensor is the Kronecker delta δij in this coordinate system. The metric tensor with respect to arbitrary (possibly curvilinear) coordinates 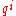 is given by:
is given by:
The round metric on a sphere
The unit sphere in R3 comes equipped with a natural metric induced from the ambient Euclidean metric. In standard spherical coordinates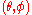 , with
, with 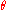 the co-latitude, the angle measured from the z axis, and
the co-latitude, the angle measured from the z axis, and  the angle from the x axis in the xy plane, the metric takes the form
the angle from the x axis in the xy plane, the metric takes the form
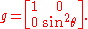
This is usually written in the form

Lorentzian metrics from relativity
In flat Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
(special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
), with coordinates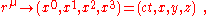 the metric is
the metric is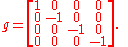
For a curve with—for example—constant time coordinate, the length formula with this metric reduces to the usual length formula. For a timelike curve, the length formula gives the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
along the curve.
In this case, the spacetime interval is written as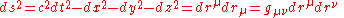 .
.
The Schwarzschild metricSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
describes the spacetime around a spherically symmetric body, such as a planet, or a black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. With coordinates , we can write the metric as
, we can write the metric as
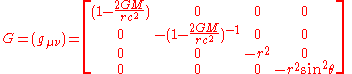
where G (inside the matrix) is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
and M the mass of the body.
See also
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Metric tensor (general relativity)Metric tensor (general relativity)In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
- List of coordinate charts
- Finsler manifoldFinsler manifoldIn mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
External links
- Caltech Tutorial on Relativity — A simple introduction to the basics of metrics in the context of relativity.
- gp is bilinear