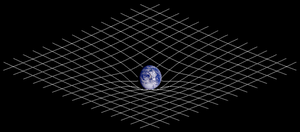
Spacetime - AbsoluteAstronomy.com

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, spacetime (or space-time, space time, space-time continuum) is any mathematical model

Mathematical model

A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...

that combines space

Space

Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...

and time

Time in physics

Time in physics is defined by its measurement: time is what a clock reads. It is a scalar quantity and, like length, mass, and charge, is usually described as a fundamental quantity. Time can be combined mathematically with other physical quantities to derive other concepts such as motion, kinetic...

into a single continuum

Continuum (theory)

Continuum theories or models explain variation as involving a gradual quantitative transition without abrupt changes or discontinuities. It can be contrasted with 'categorical' models which propose qualitatively different states.-In physics:...

. Spacetime is usually interpreted with space as being three-dimensional

Three-dimensional space

Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...

and time playing the role of a fourth dimension

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

that is of a different sort from the spatial dimensions. According to certain Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

perceptions, the universe

Universe

The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...

has three dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

s of space and one dimension of time. By combining space and time into a single manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, physicists have significantly simplified a large number of physical theories

Theoretical physics

Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...

, as well as described in a more uniform way the workings of the universe at both the supergalactic

Physical cosmology

Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...

and subatomic

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

levels.

In non-relativistic classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

, the use of Euclidean space instead of spacetime is appropriate, as time is treated as universal and constant, being independent of the state of motion of an observer. In relativistic

Theory of relativity

The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....

contexts, time cannot be separated from the three dimensions of space, because the observed rate at which time passes for an object depends on the object's velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

relative to the observer and also on the strength of gravitational fields, which can slow the passage of time.

In cosmology

Cosmology

Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...

, the concept of spacetime combines space and time to a single abstract universe

Universe

. Mathematically it is a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

consisting of "events" which are described by some type of coordinate system

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

. Typically three spatial dimensions (length, width, height), and one temporal dimension (time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

) are required. Dimensions are independent components of a coordinate grid needed to locate a point in a certain defined "space". For example, on the globe the latitude

Latitude

In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...

and longitude

Longitude

Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....

are two independent coordinates which together uniquely determine a location. In spacetime, a coordinate grid that spans the 3+1 dimensions locates events

Event (relativity)

In physics, and in particular relativity, an event indicates a physical situation or occurrence, located at a specific point in space and time. For example, a glass breaking on the floor is an event; it occurs at a unique place and a unique time, in a given frame of reference.Strictly speaking, the...

(rather than just points in space), i.e. time is added as another dimension to the coordinate grid. This way the coordinates specify where and when events occur. However, the unified nature of spacetime and the freedom of coordinate choice it allows imply that to express the temporal coordinate in one coordinate system requires both temporal and spatial coordinates in another coordinate system. Unlike in normal spatial coordinates, there are still restrictions for how measurements can be made spatially and temporally (see Spacetime intervals). These restrictions correspond roughly to a particular mathematical model which differs from Euclidean space in its manifest symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

.

Until the beginning of the 20th century, time was believed to be independent of motion, progressing at a fixed rate in all reference frame

Frame of reference

A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...

s; however, later experiments revealed that time slowed down at higher speeds of the reference frame relative to another reference frame (with such slowing called "time dilation

Time dilation

In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...

" explained in the theory of "special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

"). Many experiments have confirmed time dilation, such as atomic clock

Atomic clock

An atomic clock is a clock that uses an electronic transition frequency in the microwave, optical, or ultraviolet region of the electromagnetic spectrum of atoms as a frequency standard for its timekeeping element...

s onboard a Space Shuttle

Space Shuttle

The Space Shuttle was a manned orbital rocket and spacecraft system operated by NASA on 135 missions from 1981 to 2011. The system combined rocket launch, orbital spacecraft, and re-entry spaceplane with modular add-ons...

running slower than synchronized Earth-bound inertial clocks and the relativistic decay

Particle decay

Particle decay is the spontaneous process of one elementary particle transforming into other elementary particles. During this process, an elementary particle becomes a different particle with less mass and an intermediate particle such as W boson in muon decay. The intermediate particle then...

of muon

Muon

The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...

s from cosmic ray

Cosmic ray

Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...

showers. The duration of time can therefore vary for various events and various reference frame

Frame of reference

s.
When dimensions are understood as mere components of the grid system, rather than physical attributes of space, it is easier to understand the alternate dimensional views as being simply the result of coordinate transformations.

The term spacetime has taken on a generalized meaning beyond treating spacetime events with the normal 3+1 dimensions. It is really the combination of space and time. Other proposed spacetime theories include additional dimensions—normally spatial but there exist some speculative theories that include additional temporal dimensions and even some that include dimensions that are neither temporal nor spatial. How many dimensions are needed to describe the universe is still an open question. Speculative theories such as string theory

String theory

String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...

predict 10 or 26 dimensions (with M-theory

M-theory

In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...

predicting 11 dimensions: 10 spatial and 1 temporal), but the existence of more than four dimensions would only appear to make a difference at the subatomic level.

Spacetime in literature

Incas regarded space and time as a single concept, named pacha . The peoples of the Andes

Andes

The Andes is the world's longest continental mountain range. It is a continual range of highlands along the western coast of South America. This range is about long, about to wide , and of an average height of about .Along its length, the Andes is split into several ranges, which are separated...

have kept this understanding until now.

Arthur Schopenhauer

Arthur Schopenhauer

Arthur Schopenhauer was a German philosopher known for his pessimism and philosophical clarity. At age 25, he published his doctoral dissertation, On the Fourfold Root of the Principle of Sufficient Reason, which examined the four separate manifestations of reason in the phenomenal...

wrote in §18 of On the Fourfold Root of the Principle of Sufficient Reason
On the Fourfold Root of the Principle of Sufficient Reason
On the Fourfold Root of the Principle of Sufficient Reason was originally published as a doctoral dissertation in 1813. The German philosopher Arthur Schopenhauer revised this important work and re-published it in 1847....

(1813): "...the representation of coexistence is impossible in Time alone; it depends, for its completion, upon the representation of Space; because, in mere Time, all things follow one another, and in mere Space all things are side by side; it is accordingly only by the combination of Time and Space that the representation of coexistence arises."

The idea of a unified spacetime is stated by Edgar Allan Poe

Edgar Allan Poe

Edgar Allan Poe was an American author, poet, editor and literary critic, considered part of the American Romantic Movement. Best known for his tales of mystery and the macabre, Poe was one of the earliest American practitioners of the short story and is considered the inventor of the detective...

in his essay on cosmology titled Eureka
Eureka (Edgar Allan Poe)
Eureka is a lengthy non-fiction work by American author Edgar Allan Poe which he subtitled "A Prose Poem", though it has also been subtitled as "An Essay on the Material and Spiritual Universe". Adapted from a lecture he had presented, Eureka describes Poe's intuitive conception of the nature of...

(1848) that "Space and duration are one." In 1895, in his novel The Time Machine
The Time Machine
The Time Machine is a science fiction novella by H. G. Wells, published in 1895 for the first time and later adapted into at least two feature films of the same name, as well as two television versions, and a large number of comic book adaptations. It indirectly inspired many more works of fiction...

, H.G. Wells wrote, "There is no difference between time and any of the three dimensions of space except that our consciousness moves along it", and that "any real body must have extension in four directions: it must have Length, Breadth, Thickness, and Duration."

Mathematical concept

The first reference to spacetime as a mathematical concept was in 1754 by Jean le Rond d'Alembert

Jean le Rond d'Alembert

Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...

in the article Dimension in Encyclopedie

Encyclopédie

Encyclopédie, ou dictionnaire raisonné des sciences, des arts et des métiers was a general encyclopedia published in France between 1751 and 1772, with later supplements, revised editions, and translations. It was edited by Denis Diderot and Jean le Rond d'Alembert...

. Another early venture was by Joseph Louis Lagrange

Joseph Louis Lagrange

Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...

in his Theory of Analytic Functions (1797, 1813). He said, "One may view mechanics as a geometry of four dimensions, and mechanical analysis as an extension of geometric analysis".

After discovering quaternion

Quaternion

In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...

s, William Rowan Hamilton

William Rowan Hamilton

Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...

commented, "Time is said to have only one dimension, and space to have three dimensions. ... The mathematical quaternion partakes of both these elements; in technical language it may be said to be 'time plus space', or 'space plus time': and in this sense it has, or at least involves a reference to, four dimensions. And how the One of Time, of Space the Three, Might in the Chain

Classical Hamiltonian quaternions

William Rowan Hamilton invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties...

of Symbols girdled be." Hamilton's biquaternions, which have algebraic properties sufficient to model spacetime and its symmetry, were in play for more than a half-century before formal relativity. For instance, William Kingdon Clifford

William Kingdon Clifford

William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...

noted their relevance.

Another important antecedent to spacetime was the work of James Clerk Maxwell

James Clerk Maxwell

James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...

as he used partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

s to develop electrodynamics with the four parameters. Lorentz

Hendrik Lorentz

Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...

discovered some invariances

Lorentz transformation

In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...

of Maxwell's equations

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

late in the 19th century which were to become the basis of Einstein's theory of special relativity. Fiction authors were also in on the game, as mentioned above. It has always been the case that time and space are measured using real numbers, and the suggestion that the dimensions of space and time are comparable could have been raised by the first people to have formalized physics, but ultimately, the contradictions between Maxwell's laws and Galilean relativity had to come to a head with the realization of the import of finitude of the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

.

While spacetime can be viewed as a consequence of Albert Einstein

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

's 1905 theory of special relativity

Special relativity

, it was first explicitly proposed mathematically by one of his teachers, the mathematician Hermann Minkowski

Hermann Minkowski

Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...

, in a 1908 essay building on and extending Einstein's work. His concept of Minkowski space

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

is the earliest treatment of space and time as two aspects of a unified whole, the essence of special relativity

Special relativity

. The idea of Minkowski space also led to special relativity being viewed in a more geometrical way, this geometric viewpoint of spacetime being important in general relativity too. (For an English translation of Minkowski's article, see Lorentz et al. 1952.) The 1926 thirteenth edition of the Encyclopædia Britannica
Encyclopædia Britannica
The Encyclopædia Britannica , published by Encyclopædia Britannica, Inc., is a general knowledge English-language encyclopaedia that is available in print, as a DVD, and on the Internet. It is written and continuously updated by about 100 full-time editors and more than 4,000 expert...

included an article by Einstein titled "Space-Time".

Basic concepts

Spacetimes are the arenas in which all physical events take place—an event is a point in spacetime specified by its time and place. For example, the motion of planet

Planet

A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...

s around the sun

Sun

The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

may be described in a particular type of spacetime, or the motion of light

Light

Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...

around a rotating star

Star

A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...

may be described in another type of spacetime. The basic elements of spacetime are events. In any given spacetime, an event is a unique position at a unique time. Because events are spacetime points, an example of an event in classical relativistic physics is

, the location of an elementary (point-like) particle at a particular time. A spacetime itself can be viewed as the union of all events in the same way that a line is the union of all of its points, formally organized into a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, a space which can be described at small scales using coordinates systems.

A spacetime is independent of any observer. However, in describing physical phenomena (which occur at certain moments of time in a given region of space), each observer chooses a convenient metrical coordinate system

Coordinate system

. Events are specified by four real numbers in any such coordinate system. The trajectories of elementary (point-like) particles through space and time are thus a continuum of events called the world line

World line

In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...

of the particle. Extended or composite objects (consisting of many elementary particles) are thus a union of many worldlines twisted together by virtue of their interactions through spacetime into a "world-braid" (permitting a fascinating connection with the myth of the Moirae

Moirae

The Moirae, Moerae or Moirai , in Greek mythology, were the white-robed incarnations of destiny . Their number became fixed at three...

to be made).

However, in physics, it is common to treat an extended object as a "particle" or "field" with its own unique (e.g. center of mass) position at any given time, so that the world line of a particle or light beam is the path that this particle or beam takes in the spacetime and represents the history of the particle or beam. The world line of the orbit of the Earth (in such a description) is depicted in two spatial dimensions x and y (the plane of the Earth's orbit) and a time dimension orthogonal to x and y. The orbit of the Earth is an ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

in space alone, but its worldline is a helix

Helix

A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...

in spacetime.

The unification of space and time is exemplified by the common practice of selecting a metric (the measure that specifies the interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

between two events in spacetime) such that all four dimensions are measured in terms of units

Units of measurement

A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...

of distance: representing an event as

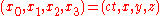(in the Lorentz metric) or

(in the original Minkowski metric) where

is the speed of light

Speed of light

. The metrical descriptions of Minkowski Space

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

and spacelike, lightlike, and timelike intervals given below follow this convention, as do the conventional formulations of the Lorentz transformation

Lorentz transformation

Spacetime intervals

In a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, the separation between two points is measured by the distance between the two points. A distance is purely spatial, and is always positive. In spacetime, the separation between two events is measured by the interval

Invariant interval

In physics, the invariant interval is the measure of separation between two arbitrarily close events in the spacetime of general or special theory of relativity. It is invariant under the coordinate transformations from the covariance group of the theory...

between the two events, which takes into account not only the spatial separation between the events, but also their temporal separation. The interval between two events is defined as:

(spacetime interval),

where c is the speed of light, and Δr and Δt denote differences of the space and time coordinates, respectively, between the events.

(Note that the choice of signs for

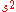above follows the space-like convention (-+++). Other treatments reverse the sign of

.)

Spacetime intervals may be classified into three distinct types based on whether the temporal separation (

) or the spatial separation (

) of the two events is greater.

Certain types of worldlines

World line

(called geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s of the spacetime) are the shortest paths between any two events, with distance being defined in terms of spacetime intervals. The concept of geodesics becomes critical in general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, since geodesic motion may be thought of as "pure motion" (inertial motion

Fictitious force

A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....

) in spacetime, that is, free from any external influences.

Time-like interval

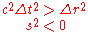
For two events separated by a time-like interval, enough time passes between them for there to be a cause-effect relationship between the two events. For a particle traveling through space at less than the speed of light, any two events which occur to or by the particle must be separated by a time-like interval. Event pairs with time-like separation define a negative squared spacetime interval (

) and may be said to occur in each other's future or past. There exists a reference frame

Frame of reference

such that the two events are observed to occur in the same spatial location, but there is no reference frame in which the two events can occur at the same time.

The measure of a time-like spacetime interval is described by the proper time

Proper time

In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...

(proper time). The proper time interval would be measured by an observer with a clock traveling between the two events in an inertial reference frame, when the observer's path intersects each event as that event occurs. (The proper time defines a real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

, since the interior of the square root is positive.)

Light-like interval

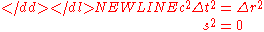
In a light-like interval, the spatial distance between two events is exactly balanced by the time between the two events. The events define a squared spacetime interval of zero (

). Light-like intervals are also known as "null" intervals.

Events which occur to or are initiated by a photon

Photon

In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...

along its path (i.e., while traveling at

, the speed of light) all have light-like separation. Given one event, all those events which follow at light-like intervals define the propagation of a light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

, and all the events which preceded from a light-like interval define a second (graphically inverted, which is to say "pastward") light cone.

Space-like interval

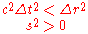
When a space-like interval separates two events, not enough time passes between their occurrences for there to exist a causal relationship crossing the spatial distance between the two events at the speed of light or slower. Generally, the events are considered not to occur in each other's future or past. There exists a reference frame

Frame of reference

such that the two events are observed to occur at the same time, but there is no reference frame in which the two events can occur in the same spatial location.

For these space-like event pairs with a positive squared spacetime interval (

), the measurement of space-like separation is the proper distance:

(proper distance).

Like the proper time of time-like intervals, the proper distance (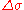

) of space-like spacetime intervals is a real number value.

Mathematics of spacetimes

For physical reasons, a spacetime continuum is mathematically defined as a four-dimensional, smooth, connected Lorentzian manifold

. This means the smooth Lorentz metric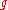

has signature

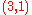. The metric determines the geometry of spacetime, as well as determining the geodesic

Geodesic

s of particles and light beams. About each point (event) on this manifold, coordinate charts are used to represent observers in reference frames. Usually, Cartesian coordinates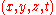

are used. Moreover, for simplicity's sake, the speed of light

is usually assumed to be unity.

A reference frame (observer) can be identified with one of these coordinate charts; any such observer can describe any event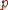

. Another reference frame may be identified by a second coordinate chart about

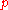. Two observers (one in each reference frame) may describe the same event

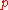but obtain different descriptions.

Usually, many overlapping coordinate charts are needed to cover a manifold. Given two coordinate charts, one containing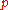

(representing an observer) and another containing

(representing another observer), the intersection of the charts represents the region of spacetime in which both observers can measure physical quantities and hence compare results. The relation between the two sets of measurements is given by a non-singular coordinate transformation on this intersection. The idea of coordinate charts as local observers who can perform measurements in their vicinity also makes good physical sense, as this is how one actually collects physical data—locally.

For example, two observers, one of whom is on Earth, but the other one who is on a fast rocket to Jupiter, may observe a comet crashing into Jupiter (this is the event

). In general, they will disagree about the exact location and timing of this impact, i.e., they will have different 4-tuples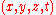

(as they are using different coordinate systems). Although their kinematic descriptions will differ, dynamical (physical) laws, such as momentum conservation and the first law of thermodynamics, will still hold. In fact, relativity theory requires more than this in the sense that it stipulates these (and all other physical) laws must take the same form in all coordinate systems. This introduces tensors into relativity, by which all physical quantities are represented.

Geodesics are said to be time-like, null, or space-like if the tangent vector to one point of the geodesic is of this nature. The paths of particles and light beams in spacetime are represented by time-like and null (light-like) geodesics (respectively).

Topology

The assumptions contained in the definition of a spacetime are usually justified by the following considerations.

The connectedness

Connectedness

In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...

assumption serves two main purposes. First, different observers making measurements (represented by coordinate charts) should be able to compare their observations on the non-empty intersection of the charts. If the connectedness assumption were dropped, this would not be possible. Second, for a manifold, the properties of connectedness and path-connectedness are equivalent and, one requires the existence of paths (in particular, geodesic

Geodesic

s) in the spacetime to represent the motion of particles and radiation.

Every spacetime is paracompact. This property, allied with the smoothness of the spacetime, gives rise to a smooth linear connection

Connection (principal bundle)

In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...

, an important structure in general relativity. Some important theorems on constructing spacetimes from compact and non-compact manifolds include the following:

A compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

manifold can be turned into a spacetime if, and only if, its Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

is 0. (Proof idea: the existence of a Lorentzian metric is shown to be equivalent to the existence of a nonvanishing vector field.)
Any non-compact 4-manifold can be turned into a spacetime.

Spacetime symmetries

Often in relativity, spacetimes that have some form of symmetry are studied. As well as helping to classify spacetimes, these symmetries usually serve as a simplifying assumption in specialized work. Some of the most popular ones include:

Axisymmetric spacetimes
Spherically symmetric spacetime
Spherically symmetric spacetime
A spherically symmetric spacetime is a spacetime whose isometry group contains a subgroup which is isomorphic to the group SO and the orbits of this group are 2-dimensional spheres . The isometries are then interpreted as rotations and a spherically symmetric spacetime is often described as one...

s
Static spacetime
Static spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...

s
Stationary spacetime
Stationary spacetime
In general relativity, specifically in the Einstein field equations, a spacetime is said to be stationary if it admits a Killing vector that is asymptotically timelike....

s.

Causal structure

The causal structure of a spacetime describes causal relationships between pairs of points in the spacetime based on the existence of certain types of curves joining the points.

Spacetime in special relativity

The geometry of spacetime in special relativity is described by the Minkowski metric on R⁴. This spacetime is called Minkowski space. The Minkowski metric is usually denoted by

and can be written as a four-by-four matrix:

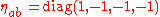
where the Landau–Lifshitz space-like convention is being used. A basic assumption of relativity is that coordinate transformations must leave spacetime intervals invariant. Intervals are invariant under Lorentz transformation

Lorentz transformation

s. This invariance property leads to the use of four-vector

Four-vector

In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...

s (and other tensors) in describing physics.

Strictly speaking, one can also consider events in Newtonian physics as a single spacetime. This is Galilean-Newtonian relativity, and the coordinate systems are related by Galilean transformation

Galilean transformation

The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...

s. However, since these preserve spatial and temporal distances independently, such a spacetime can be decomposed into spatial coordinates plus temporal coordinates, which is not possible in the general case.

Spacetime in general relativity

In general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, it is assumed that spacetime is curved by the presence of matter (energy), this curvature being represented by the Riemann tensor. In special relativity

Special relativity

, the Riemann tensor is identically zero, and so this concept of "non-curvedness" is sometimes expressed by the statement Minkowski spacetime is flat.

The earlier discussed notions of time-like, light-like and space-like intervals in special relativity can similarly be used to classify one-dimensional curves through curved spacetime. A time-like curve can be understood as one where the interval between any two infinitesimal

Infinitesimal

Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...

ly close events on the curve is time-like, and likewise for light-like and space-like curves. Technically the three types of curves are usually defined in terms of whether the tangent vector at each point on the curve is time-like, light-like or space-like. The world line

World line

of a slower-than-light object will always be a time-like curve, the world line of a massless particle such as a photon will be a light-like curve, and a space-like curve could be the world line of a hypothetical tachyon

Tachyon

A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...

. In the local neighborhood of any event, time-like curves that pass through the event will remain inside that event's past and future light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

s, light-like curves that pass through the event will be on the surface of the light cones, and space-like curves that pass through the event will be outside the light cones. One can also define the notion of a 3-dimensional "spacelike hypersurface", a continuous 3-dimensional "slice" through the 4-dimensional property with the property that every curve that is contained entirely within this hypersurface is a space-like curve.

Many spacetime continua have physical interpretations which most physicists would consider bizarre or unsettling. For example, a compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

spacetime has closed timelike curve

Closed timelike curve

In mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...

s, which violate our usual ideas of causality (that is, future events could affect past ones). For this reason, mathematical physicists usually consider only restricted subsets of all the possible spacetimes. One way to do this is to study "realistic" solutions of the equations of general relativity. Another way is to add some additional "physically reasonable" but still fairly general geometric restrictions and try to prove interesting things about the resulting spacetimes. The latter approach has led to some important results, most notably the Penrose–Hawking singularity theorems.

Quantized spacetime

In general relativity, spacetime is assumed to be smooth and continuous—and not just in the mathematical sense. In the theory of quantum mechanics, there is an inherent discreteness present in physics. In attempting to reconcile these two theories, it is sometimes postulated that spacetime should be quantized at the very smallest scales. Current theory is focused on the nature of spacetime at the Planck scale

Planck scale

In particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...

. Causal sets

Causal sets

The causal sets programme is an approach to quantum gravity. Its founding principle is that spacetime is fundamentally discrete and that the spacetime events are related by a partial order...

, loop quantum gravity

Loop quantum gravity

Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...

, string theory

String theory

, and black hole thermodynamics

Black hole thermodynamics

In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...

all predict a quantized

Quantization (physics)

In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...

spacetime with agreement on the order of magnitude. Loop quantum gravity makes precise predictions about the geometry of spacetime at the Planck scale.

Privileged character of 3+1 spacetime

There are two kinds of dimensions, spatial (bidirectional) and temporal (unidirectional). Let the number of spatial dimensions be N and the number of temporal dimensions be T. That N = 3 and T = 1, setting aside the compactified dimensions invoked by string theory

String theory

and undetectable to date, can be explained by appealing to the physical consequences of letting N differ from 3 and T differ from 1. The argument is often of an anthropic

Anthropic principle

In astrophysics and cosmology, the anthropic principle is the philosophical argument that observations of the physical Universe must be compatible with the conscious life that observes it. Some proponents of the argument reason that it explains why the Universe has the age and the fundamental...

character.

Immanuel Kant

Immanuel Kant

Immanuel Kant was a German philosopher from Königsberg , researching, lecturing and writing on philosophy and anthropology at the end of the 18th Century Enlightenment....

argued that 3-dimensional space was a consequence of the inverse square law of universal gravitation. While Kant's argument is historically important, John D. Barrow

John D. Barrow

-External links:****** The Forum-Publications available on the Internet:************...

says that it "...gets the punch-line back to front: it is the three-dimensionality of space that explains why we see inverse-square force laws in Nature, not vice-versa." (Barrow 2002: 204). This is because the law of gravitation (or any other inverse-square law

Inverse-square law

In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....

) follows from the concept of flux

Flux

In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...

and the proportional relationship of flux density and the strength of field. If N = 3, then 3-dimensional solid objects have surface areas proportional to the square of their size in any selected spatial dimension. In particular, a sphere of radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

r has area of 4πr ². More generally, in a space of N dimensions, the strength of the gravitational attraction between two bodies separated by a distance of r would be inversely proportional to r^N−1.

In 1920, Paul Ehrenfest

Paul Ehrenfest

Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...

showed that if we fix T = 1 and let N > 3, the orbit

Orbit

In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...

of a planet

Planet

about its sun cannot remain stable. The same is true of a star's orbit around the center of its galaxy

Galaxy

A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...

. Ehrenfest also showed that if N is even, then the different parts of a wave

Wave

In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...

impulse will travel at different speeds. If N > 3 and odd, then wave impulses become distorted. Only when N = 3 or 1 are both problems avoided. In 1922, Hermann Weyl

Hermann Weyl

Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...

showed that Maxwell

James Clerk Maxwell

's theory of electromagnetism

Electromagnetism

Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...

works only when N = 3 and T = 1, writing that this fact "...not only leads to a deeper understanding of Maxwell's theory, but also of the fact that the world is four dimensional, which has hitherto always been accepted as merely 'accidental,' become intelligible through it."
Finally, Tangherlini showed in 1963 that when N > 3, electron orbitals

Atomic orbital

An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...

around nuclei cannot be stable; electrons would either fall into the nucleus

Atomic nucleus

The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...

or disperse.
Max Tegmark

Max Tegmark

Max Tegmark is a Swedish-American cosmologist. Tegmark is a professor at the Massachusetts Institute of Technology and belongs to the scientific directorate of the Foundational Questions Institute.-Early life:...

expands on the preceding argument in the following anthropic

Anthropic principle

manner. If T differs from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equation

Partial differential equation

s. In such a universe, intelligent life capable of manipulating technology could not emerge. Moreover, if T > 1, Tegmark maintains that proton

Proton

The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....

s and electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

s would be unstable and could decay into particles having greater mass than themselves. (This is not a problem if the particles have a sufficiently low temperature.) If N > 3, Ehrenfest's argument above holds; atoms as we know them (and probably more complex structures as well) could not exist. If N < 3, gravitation of any kind becomes problematic, and the universe is probably too simple to contain observers. For example, when N < 3, nerves cannot cross without intersecting.

In general, it is not clear how physical law could function if T differed from 1. If T > 1, subatomic particles which decay after a fixed period would not behave predictably, because time-like geodesic

Geodesic

s would not be necessarily maximal. N = 1 and T = 3 has the peculiar property that the speed of light

Speed of light

in a vacuum is a lower bound on the velocity of matter; all matter consists of tachyon

Tachyon

s.

Hence anthropic and other arguments rule out all cases except N = 3 and T = 1—which happens to describe the world about us. Curiously, the cases N = 3 or 4 have the richest and most difficult geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

and topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

. There are, for example, geometric statements whose truth or falsity is known for all N except one or both of 3 and 4. N = 3 was the last case of the Poincaré conjecture

Poincaré conjecture

In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...

to be proved.

For an elementary treatment of the privileged status of N = 3 and T = 1, see chpt. 10 (esp. Fig. 10.12) of Barrow; for deeper treatments, see §4.8 of Barrow and Tipler (1986) and Tegmark. Barrow has repeatedly cited the work of Whitrow

Gerald James Whitrow

Gerald James Whitrow was a British mathematician, cosmologist and science historian.After completing school at Christ's Hospital, he obtained a scholarship at Christ Church, Oxford in 1930, earning his first degree in 1933, the MA in 1937, and the PhD in 1939...

.

String theory

String theory

hypothesizes that matter and energy are composed of tiny vibrating strings of various types, most of which are embedded in dimensions that exist only on a scale no larger than the Planck length. Hence N = 3 and T = 1 do not characterize string theory, which embeds vibrating strings in coordinate grids having 10, or even 26, dimensions.

The Causal dynamical triangulation (CDT) theory is a background independent theory which derives the observed 3+1 spacetime from a minimal set of assumptions, and needs no adjusting factors. It does not assume any pre-existing arena (dimensional space), but rather attempts to show how the spacetime fabric itself evolves. It shows spacetime to be 2-d near the Planck scale

Planck scale

In particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...

, and reveals a fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

structure on slices of constant time, but spacetime becomes 3+1-d in scales significantly larger than Planck. So, CDT may become the first theory which doesn't postulate but really explains observed number of spacetime dimensions.

External links

Stanford Encyclopedia of Philosophy
Stanford Encyclopedia of Philosophy
The Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...

: "Space and Time: Inertial Frames" by Robert DiSalle.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.