Nonlinearity
Encyclopedia
- This article describes the use of the term nonlinearity in mathematics. For other meanings, see nonlinearity (disambiguation)Nonlinearity (disambiguation)Nonlinear generally refers to a situation that has a disproportionate cause and effect.In science and mathematics, nonlinearity can refer to:* Nonlinear optics, in physics, examines the properties of light in media in which the polarization responds nonlinearly to the electric field.* Nonlinear...
.
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a nonlinear system is one that does not satisfy the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, or one whose output is not directly proportional to its input; a linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
fulfills these conditions. In other words, a nonlinear system is any problem where the variable(s) to be solved for cannot be written as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of independent components. A nonhomogeneous
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
system, which is linear apart from the presence of a function of the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s, is nonlinear according to a strict definition, but such systems are usually studied alongside linear systems, because they can be transformed to a linear system of multiple variables.
Nonlinear problems are of interest to engineer
Engineer
An engineer is a professional practitioner of engineering, concerned with applying scientific knowledge, mathematics and ingenuity to develop solutions for technical problems. Engineers design materials, structures, machines and systems while considering the limitations imposed by practicality,...
s, physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
s and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s because most physical systems are inherently nonlinear in nature. Nonlinear equations are difficult to solve and give rise to interesting phenomena such as chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
. The weather is famously chaotic, where simple changes in one part of the system produce complex effects throughout.
Definition
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a linear function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(or map)
 is one which satisfies both of the following properties:
is one which satisfies both of the following properties:
- additivity,

- homogeneity,

(Additivity implies homogeneity for any rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
α, and, for continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s, for any real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
α. For a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
α, homogeneity does not follow from additivity; for example, an antilinear map is additive but not homogeneous.) The conditions of additivity and homogeneity are often combined in the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...

An equation written as

is called linear if
 is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if
is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if  .
.The definition
 is very general in that
is very general in that  can be any sensible mathematical object (number, vector, function, etc.), and the function
can be any sensible mathematical object (number, vector, function, etc.), and the function  can literally be any mapping
can literally be any mappingMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
, including integration or differentiation with associated constraints (such as boundary values). If
 contains differentiation
contains differentiationDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
 , the result will be a differential equation
, the result will be a differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
.
Nonlinear algebraic equations
Nonlinear algebraic equations, which are also called polynomial equations, are defined by equating polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s to zero. For example,

For a single polynomial equation, root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
s can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However,
systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a difficult branch of modern mathematics. It is even difficult to decide if a given algebraic system has complex solutions (see Hilbert's Nullstellensatz
Hilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
). Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
are now well understood and efficient methods exist for solving them.
Nonlinear recurrence relations
A nonlinear recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
defines successive terms of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
and the relations that define the various Hofstadter sequence
Hofstadter sequence
In mathematics, a Hofstadter sequence is a member of a family of related integer sequences defined by non-linear recurrence relations.-Sequences presented in Gödel, Escher, Bach: an Eternal Golden Braid:...
s.
Nonlinear differential equations
A systemSimultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s is said to be nonlinear if it is not a linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics, the Lotka–Volterra equations in biology, and the Black–Scholes PDE in finance.
One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
prevents the construction of new solutions.
Ordinary differential equations
First order ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s are often exactly solvable by separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, especially for autonomous equations. For example, the nonlinear equation

will easily yield u = (x + C)−1 as a general solution. The equation is nonlinear because it may be written as

and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u2 term were replaced with u, the problem would be linear (the exponential decay problem).
Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed form
Closed form
-Maths:* Closed-form expression, a finitary expression* Closed differential form, a differential form \alpha with the property that d\alpha = 0-Poetry:* In poetry analysis, a type of poetry that exhibits regular structure, such as meter or a rhyming pattern;...
solutions, though implicit solutions and solutions involving nonelementary integral
Nonelementary integral
In mathematics, a nonelementary antiderivative is an antiderivative for which it can be shown that there exists no formula in terms of elementary functions . A theorem by Liouville in 1835 provided the first proof that nonelementary antiderivatives exist...
s are encountered.
Common methods for the qualitative analysis of nonlinear ordinary differential equations include:
- Examination of any conserved quantities, especially in Hamiltonian systemHamiltonian systemIn physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
s. - Examination of dissipative quantities (see Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
) analogous to conserved quantities. - Linearization via Taylor expansion.
- Change of variables into something easier to study.
- Bifurcation theoryBifurcation theoryBifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
. - PerturbationPerturbation theoryPerturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
methods (can be applied to algebraic equations too).
Partial differential equations
The most common basic approach to studying nonlinear partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, as seen in the similarity transform or separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, which is always useful whether or not the resulting ordinary differential equation(s) is solvable.
Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis
Scale analysis (mathematics)
Scale analysis is a powerful tool used in the mathematical sciences for the simplification of equations with many terms. First the approximate magnitude of individual terms in the equations is determined...
to simplify a general, natural equation in a certain specific boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
. For example, the (very) nonlinear Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation.
Other methods include examining the characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
and using the methods outlined above for ordinary differential equations.
Pendula

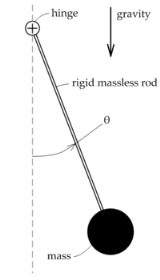
Pendulum (mathematics)
The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.- Simple gravity pendulum :...
under influence of gravity. Using Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, it may be shown that the motion of a pendulum can be described by the dimensionless nonlinear equation
 (one should note that in this equation g = L = 1)
(one should note that in this equation g = L = 1)where gravity points "downwards" and
 is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use
is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use  as an integrating factor
as an integrating factorIntegrating factor
In mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus, in this case often multiplying through by an...
, which would eventually yield

which is an implicit solution involving an elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral
Nonelementary integral
In mathematics, a nonelementary antiderivative is an antiderivative for which it can be shown that there exists no formula in terms of elementary functions . A theorem by Liouville in 1835 provided the first proof that nonelementary antiderivatives exist...
(nonelementary even if
 ).
).Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at
 , called the small angle approximation, is
, called the small angle approximation, is
since
 for
for  . This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at
. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at  , corresponding to the pendulum being straight up:
, corresponding to the pendulum being straight up:
since
 for
for  . The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that
. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that  will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.
will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.One more interesting linearization is possible around
 , around which
, around which  :
:
This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact) phase portrait
Phase portrait
A phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is representated by a different curve, or point....
s and approximate periods.
Types of nonlinear behaviors
- IndeterminismIndeterminismIndeterminism is the concept that events are not caused, or not caused deterministically by prior events. It is the opposite of determinism and related to chance...
- the behavior of a system cannot be predicted. - Multistability - alternating between two or more exclusive states.
- Aperiodic oscillations - functions that do not repeat values after some period (otherwise known as chaotic oscillations or chaos).
Examples of nonlinear equations
See also the list of nonlinear partial differential equationsSoftware for solving nonlinear system
- interalg: solver from OpenOptOpenOptOpenOpt is an open-source framework for numerical optimization, nonlinear equations and systems of them. It is licensed under the BSD license, making it available to be used in both open- and closed-code software. The package already has some essential ....
/ FuncDesignerFuncDesignerFuncDesigner is a computer algebra system written as a Python module. It is cross-platform software , with a completely free license....
frameworks for searching either any or all solutions of nonlinear algebraic equations system - A collection of non-linear models and demo applets (in Monash University's Virtual Lab)
- FyDiK Software for simulations of nonlinear dynamical systems
See also
- InteractionInteractionInteraction is a kind of action that occurs as two or more objects have an effect upon one another. The idea of a two-way effect is essential in the concept of interaction, as opposed to a one-way causal effect...
- Aleksandr Mikhailovich Lyapunov
- Dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
- Linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
- Mode couplingMode couplingIn the term mode coupling, as used in physics and electrical engineering, the word "mode" refers to eigenmodes of an idealized, "unperturbed", linear system. Most often, these eigenmodes are plane waves...
- Volterra seriesVolterra SeriesThe Volterra series is a model for non-linear behavior similar to the Taylor series. It differs from the Taylor series in its ability to capture 'memory' effects. The Taylor series can be used to approximate the response of a nonlinear system to a given input if the output of this system depends...
- Vector solitonVector solitonIn physical optics or wave optics, a vector soliton is a solitary wave with multiple components coupled together that maintains its shape during propagation. Ordinary solitons maintain their shape but have effectively only one polarization component, while vector solitons have two distinct...
External links
- Command and Control Research Program (CCRP)
- New England Complex Systems Institute: Concepts in Complex Systems
- Nonlinear Dynamics I: Chaos at MIT's OpenCourseWare
- Nonlinear Models Nonlinear Model Database of Physical Systems (MATLAB)
- The Center for Nonlinear Studies at Los Alamos National Laboratory

