Riemannian geometry - AbsoluteAstronomy.com

Riemannian geometry is the branch of differential geometry that studies Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

s, smooth manifolds

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

with a Riemannian metric, i.e. with an inner product on the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

at each point which varies smoothly

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

from point to point. This gives, in particular, local notions of angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

, length of curves

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

, surface area

Surface area

Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...

, and volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

. From those some other global quantities can be derived by integrating

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

local contributions.

Riemannian geometry originated with the vision of Bernhard Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

expressed in his inaugurational lecture Ueber die Hypothesen, welche der Geometrie zu Grunde liegen (English: On the hypotheses on which geometry is based). It is a very broad and abstract generalization of the differential geometry of surfaces

Differential geometry of surfaces

In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....

in R³. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s on them, with techniques that can be applied to the study of differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

s of higher dimensions. It enabled Einstein

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

's general relativity theory, made profound impact on group theory

Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

and representation theory

Representation theory

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

, as well as analysis, and spurred the development of algebraic

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

and differential topology

Differential topology

In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...

Introduction

Riemannian geometry was first put forward in generality by Bernhard Riemann

Bernhard Riemann

in the nineteenth century. It deals with a broad range of geometries whose metric properties vary from point to point, as well as two standard types of Non-Euclidean geometry

Non-Euclidean geometry

Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...

, spherical geometry

Spherical geometry

Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....

and hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

, as well as Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

itself.

Any smooth manifold admits a Riemannian metric, which often helps to solve problems of differential topology

Differential topology

. It also serves as an entry level for the more complicated structure of pseudo-Riemannian manifold

Pseudo-Riemannian manifold

In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...

s, which (in four dimensions) are the main objects of the theory of general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

. Other generalizations of Riemannian
geometry include Finsler geometry

Finsler manifold

In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...

and spray spaces.

There exists a close analogy of differential geometry with the mathematical structure of defects in regular crystals.
Dislocations and Disclination

Disclination

A disclination is a line defect in which rotational symmetry is violated. In analogy with dislocations in crystals, the term, disinclination, for liquid crystals first used by F. C. Frank and since then has been modified to its current usage, disclination.It is a defect in the orientation of...

s produce torsions an curvature.

The following articles provide some useful introductory material:

Metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
Curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
Curvature tensor
Curvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
List of differential geometry topics
Glossary of Riemannian and metric geometry
Glossary of Riemannian and metric geometry
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology....

.

Classical theorems in Riemannian geometry

What follows is an incomplete list of the most classical theorems in Riemannian geometry. The choice is made depending on its importance, beauty, and simplicity of formulation. Most of the results can be found in the classic monograph by Jeff Cheeger

Jeff Cheeger

Jeff Cheeger , is a mathematician. Cheeger is professor at the Courant Institute of Mathematical Sciences at New York University in New York City. His main interests are differential geometry and its applications to topology and analysis.-Biography:He graduated from Harvard University with a B.A....

and D. Ebin (see below).

The formulations given are far from being very exact or the most general.
This list is oriented to those who already know the basic definitions and want to know what these definitions are about.

General theorems

Gauss–Bonnet theorem
Gauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...

The integral of the Gauss curvature on a compact 2-dimensional Riemannian manifold is equal to where denotes the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

of M. This theorem has a generalization to any compact even-dimensional Riemannian manifold, see generalized Gauss-Bonnet theorem
Generalized Gauss-Bonnet theorem
In mathematics, the generalized Gauss–Bonnet theorem presents the Euler characteristic of a closed even-dimensional Riemannian manifold as an integral of a certain polynomial derived from its curvature...

.
Nash embedding theorem
Nash embedding theorem
The Nash embedding theorems , named after John Forbes Nash, state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path...

s also called fundamental theorems of Riemannian geometry
Fundamental theorem of Riemannian geometry
In Riemannian geometry, the fundamental theorem of Riemannian geometry states that on any Riemannian manifold there is a unique torsion-free metric connection, called the Levi-Civita connection of the given metric...

. They state that every Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

can be isometrically embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

Rⁿ.

Geometry in large

In all of the following theorems we assume some local behavior of the space (usually formulated using curvature assumption) to derive some information about the global structure of the space, including either some information on the topological type of the manifold or on the behavior of points at "sufficiently large" distances.

Pinched sectional curvature

Sphere theorem
Sphere theorem
In Riemannian geometry, the sphere theorem, also known as the quarter-pinched sphere theorem, strongly restricts the topology of manifolds admitting metrics with a particular curvature bound. The precise statement of the theorem is as follows...

. If M is a simply conneced compact n-dimensional Riemannian manifold with sectional curvature strictly pinched between 1/4 and 1 then M is diffeomorphic to a sphere.
Cheeger's finiteness theorem. Given constants C, D and V, there are only finitely many (up to diffeomorphism) compact n-dimensional Riemannian manifolds with sectional curvature , diameter and volume .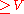
Gromov's almost flat manifolds. There is an such that if an n-dimensional Riemannian manifold has a metric with sectional curvature and diameter then its finite cover is diffeomorphic to a nil manifold.

Sectional curvature bounded below

Cheeger-Gromoll's Soul theorem
Soul theorem
In mathematics, the soul theorem is a theorem of Riemannian geometry that largely reduces the study of complete manifolds of non-negative sectional curvature to that of the compact case. Cheeger and Gromoll proved the theorem in 1972 by generalizing a 1969 result of Gromoll and Meyer...

. If M is a non-compact complete non-negatively curved n-dimensional Riemannian manifold, then M contains a compact, totally geodesic submanifold S such that M is diffeomorphic to the normal bundle of S (S is called the soul of M.) In particular, if M has strictly positive curvature everywhere, then it is diffeomorphic to Rⁿ. G. Perelman in 1994 gave an astonishingly elegant/short proof of the Soul Conjecture: M is diffeomorphic to Rⁿ if it has positive curvature at only one point.
Gromov's Betti number theorem. There is a constant C=C(n) such that if M is a compact connected n-dimensional Riemannian manifold with positive sectional curvature then the sum of its Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....

s is at most C.
Grove–Petersen's finiteness theorem. Given constants C, D and V, there are only finitely many homotopy types of compact n-dimensional Riemannian manifolds with sectional curvature , diameter and volume .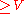

Sectional curvature bounded above

The Cartan–Hadamard theorem
Cartan–Hadamard theorem
The Cartan–Hadamard theorem is a statement in Riemannian geometry concerning the structure of complete Riemannian manifolds of non-positive sectional curvature. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space via the exponential map at any point...

states that a complete simply connected Riemannian manifold M with nonpositive sectional curvature is diffeomorphic to the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

R^n with n = dim M via the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....

at any point. It implies that any two points of a simply connected complete Riemannian manifold with nonpositive sectional curvature are joined by a unique geodesic.
The geodesic flow of any compact Riemannian manifold with negative sectional curvature is ergodic.
If M is a complete Riemannian manifold with sectional curvature bounded above by a strictly negative constant k then it is a CAT(k) space
CAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...

. Consequently, its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

Γ = π₁(M) is Gromov hyperbolic
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...

. This has many implications for the structure of the fundamental group:

it is finitely presented;
the word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...

for Γ has a positive solution;
the group Γ has finite virtual cohomological dimension
Cohomological dimension
In abstract algebra, cohomological dimension is an invariant which measures the homological complexity of representations of a group. It has important applications in geometric group theory, topology, and algebraic number theory....

;
it contains only finitely many conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

es of elements of finite order;
the abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

subgroups of Γ are virtually cyclic, so that it does not contain a subgroup isomorphic to Z×Z.

Ricci curvature bounded below

Myers theorem. If a compact Riemannian manifold has positive Ricci curvature then its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

is finite.
Splitting theorem. If a complete n-dimensional Riemannian manifold has nonnegative Ricci curvature and a straight line (i.e. a geodesic which minimizes distance on each interval) then it is isometric to a direct product of the real line and a complete (n-1)-dimensional Riemannian manifold which has nonnegative Ricci curvature.
Bishop–Gromov inequality
Bishop–Gromov inequality
In mathematics, the Bishop–Gromov inequality is a comparison theorem in Riemannian geometry, named after Richard L. Bishop and Mikhail Gromov. It is closely related to Myers' theorem, and is the key point in the proof of Gromov's compactness theorem....

. The volume of a metric ball of radius r in a complete n-dimensional Riemannian manifold with positive Ricci curvature has volume at most that of the volume of a ball of the same radius r in Euclidean space.
Gromov's compactness theorem
Gromov's compactness theorem (geometry)
In Riemannian geometry, Gromov's compactness theorem states thatthe set of Riemannian manifolds of a given dimension, with Ricci curvature ≥ c and diameter ≤ D is relatively compact in the Gromov-Hausdorff metric. It was proved by Mikhail Gromov....

. The set of all Riemannian manifolds with positive Ricci curvature and diameter at most D is pre-compact
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

in the Gromov-Hausdorff metric
Gromov-Hausdorff convergence
In mathematics, Gromov–Hausdorff convergence, named after Mikhail Gromov and Felix Hausdorff, is a notion for convergence of metric spaces which is a generalization of Hausdorff convergence.-Gromov–Hausdorff distance:...

.

Negative Ricci curvature

The isometry group
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

of a compact Riemannian manifold with negative Ricci curvature is discrete
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...

.
Any smooth manifold of dimension admits a Riemannian metric with negative Ricci curvature. (This is not true for surfaces.)

Positive scalar curvature

The n-dimensional torus does not admit a metric with positive scalar curvature.
If the injectivity radius
Glossary of Riemannian and metric geometry
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology....

of a compact n-dimensional Riemannian manifold is then the average scalar curvature is at most n(n-1).