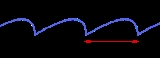
Periodic function
Encyclopedia
In mathematics
, a periodic function is a function
that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillation
s, wave
s, and other phenomena that exhibit periodicity
. Any function which is not periodic is called aperiodic.
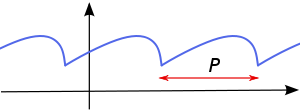
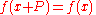
for all values of x. If there exists a least positive
constant P with this property, it is called the prime period. A function with period P will repeat on intervals of length P, and these intervals
are sometimes also referred to as periods.
Geometrically, a periodic function can be defined as a function whose graph exhibits translational symmetry
. Specifically, a function f is periodic with period P if the graph of f is invariant
under translation
in the x-direction by a distance of P. This definition of periodic can be extended to other geometric shapes and patterns, such as periodic tessellation
s of the plane.
A function that is not periodic is called aperiodic.
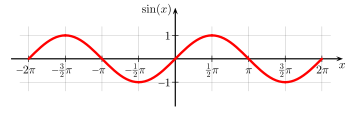For example, the sine function is periodic with period 2π, since
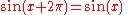
for all values of x. This function repeats on intervals of length 2π (see the graph to the right).
Everyday examples are seen when the variable is time; for instance the hands of a clock
or the phases of the moon
show periodic behaviour. Periodic motion is motion in which the position(s) of the system are expressible as periodic functions, all with the same period.
For a function on the real number
s or on the integer
s, that means that the entire graph
can be formed from copies of one particular portion, repeated at regular intervals.
A simple example of a periodic function is the function f that gives the "fractional part" of its argument. Its period is 1. In particular,
The graph of the function f is the sawtooth wave
.
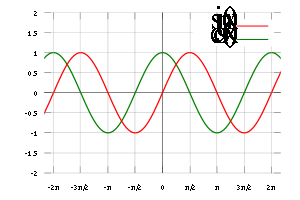The trigonometric function
s sine and cosine are common periodic functions, with period 2π (see the figure on the right). The subject of Fourier series
investigates the idea that an 'arbitrary' periodic function is a sum of trigonometric functions with matching periods.
According to the definition above, some exotic functions, for example the Dirichlet function, are also periodic; in the case of Dirichlet function, any nonzero rational number is a period.
If f(x) is a function with period P, then f(ax+b), where a is a positive constant, is periodic with period P/a. For example, f(x)=sinx has period 2π, therefore sin(5x) will have period 2π/5.
s can have two incommensurate periods without being constant. The elliptic function
s are such functions.
("Incommensurate" in this context means not real multiples of each other.)
we have the common period function:
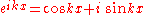
As you can see, since the cosine and sine functions are periodic, and the complex exponential above is made up of cosine/sine waves, then the above (actually Euler's formula
) has the following property. If L is the period of the function then:
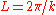
s and Floquet theory, which govern the solution of various periodic differential equations. In this context, the solution (in one dimension) is typically a function of the form:
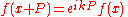
where k is a real or complex number (the Bloch wavevector or Floquet exponent). Functions of this form are sometimes called Bloch-periodic in this context. A periodic function is the special case k = 0, and an antiperiodic function is the special case k = π/P.
you encounter the problem, that Fourier series
represent periodic functions
and that Fourier series satisfy convolution theorem
s
(i.e. convolution
of Fourier series corresponds to multiplication of represented periodic function and vice versa),
but periodic functions cannot be convolved with the usual definition,
since the involved integrals diverge.
A possible way out is to define a periodic function on a bounded but periodic domain.
To this end you can use the notion of a quotient space
:
.
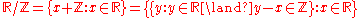That is, each element in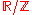
is an equivalence class
of real number
s that share the same fractional part
.
Thus a function like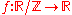
is a representation of a 1-periodic function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a periodic function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s, wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s, and other phenomena that exhibit periodicity
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
. Any function which is not periodic is called aperiodic.
Definition
A function f is said to be periodic with period P if (for some nonzero constant P) we have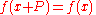for all values of x. If there exists a least positive
constant P with this property, it is called the prime period. A function with period P will repeat on intervals of length P, and these intervals
are sometimes also referred to as periods.
Geometrically, a periodic function can be defined as a function whose graph exhibits translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. Specifically, a function f is periodic with period P if the graph of f is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
in the x-direction by a distance of P. This definition of periodic can be extended to other geometric shapes and patterns, such as periodic tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s of the plane.
A function that is not periodic is called aperiodic.
Examples
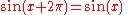
for all values of x. This function repeats on intervals of length 2π (see the graph to the right).
Everyday examples are seen when the variable is time; for instance the hands of a clock
Clock
A clock is an instrument used to indicate, keep, and co-ordinate time. The word clock is derived ultimately from the Celtic words clagan and clocca meaning "bell". A silent instrument missing such a mechanism has traditionally been known as a timepiece...
or the phases of the moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
show periodic behaviour. Periodic motion is motion in which the position(s) of the system are expressible as periodic functions, all with the same period.
For a function on the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or on the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, that means that the entire graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
can be formed from copies of one particular portion, repeated at regular intervals.
A simple example of a periodic function is the function f that gives the "fractional part" of its argument. Its period is 1. In particular,
- f( 0.5 ) = f( 1.5 ) = f( 2.5 ) = ... = 0.5.
The graph of the function f is the sawtooth wave
Sawtooth wave
The sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
.
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s sine and cosine are common periodic functions, with period 2π (see the figure on the right). The subject of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
investigates the idea that an 'arbitrary' periodic function is a sum of trigonometric functions with matching periods.
According to the definition above, some exotic functions, for example the Dirichlet function, are also periodic; in the case of Dirichlet function, any nonzero rational number is a period.
Properties
If a function f is periodic with period P, then for all x in the domain of f and all integers n,- f(x + nP) = f(x).
If f(x) is a function with period P, then f(ax+b), where a is a positive constant, is periodic with period P/a. For example, f(x)=sinx has period 2π, therefore sin(5x) will have period 2π/5.
Double-periodic functions
A function whose domain is the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s can have two incommensurate periods without being constant. The elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s are such functions.
("Incommensurate" in this context means not real multiples of each other.)
Complex example
Using complex variablesComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
we have the common period function:
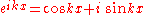
As you can see, since the cosine and sine functions are periodic, and the complex exponential above is made up of cosine/sine waves, then the above (actually Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
) has the following property. If L is the period of the function then:
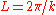
Antiperiodic functions
One common generalization of periodic functions is that of antiperiodic functions. This is a function f such that f(x + P) = −f(x) for all x. (Thus, a P-antiperiodic function is a 2P-periodic function.)Bloch-periodic functions
A further generalization appears in the context of Bloch waveBloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
s and Floquet theory, which govern the solution of various periodic differential equations. In this context, the solution (in one dimension) is typically a function of the form:
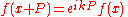
where k is a real or complex number (the Bloch wavevector or Floquet exponent). Functions of this form are sometimes called Bloch-periodic in this context. A periodic function is the special case k = 0, and an antiperiodic function is the special case k = π/P.
Quotient spaces as domain
In signal processingSignal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
you encounter the problem, that Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
represent periodic functions
and that Fourier series satisfy convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
s
(i.e. convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of Fourier series corresponds to multiplication of represented periodic function and vice versa),
but periodic functions cannot be convolved with the usual definition,
since the involved integrals diverge.
A possible way out is to define a periodic function on a bounded but periodic domain.
To this end you can use the notion of a quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
:
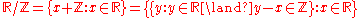.That is, each element in
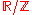is an equivalence classof real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s that share the same fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
.
Thus a function like
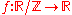
is a representation of a 1-periodic function.
See also
- Periodic sequencePeriodic sequenceIn mathematics, a periodic sequence is a sequence for which the same terms are repeated over and over:The number p of repeated terms is called the period.-Definition:A periodic sequence is a sequence a1, a2, a3, ... satisfying...
- Almost periodic functionAlmost periodic functionIn mathematics, an almost periodic function is, loosely speaking, a function of a real number that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov,...
- AmplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
- Definite pitch
- Doubly periodic function
- Floquet theory
- FrequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
- OscillationOscillationOscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
- Quasiperiodic functionQuasiperiodic functionIn mathematics, a function is said to be quasiperiodic when it has some similarity to a periodic function but does not meet the strict definition.A simple case is if the function obeys the equation:...
- WavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
- Periodic summation