Euclidean space - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Euclidean space is the Euclidean plane and three-dimensional space

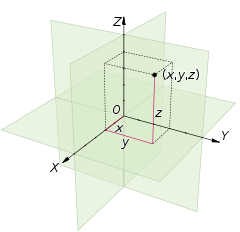
Three-dimensional space

Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...

of Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

, as well as the generalizations of these notions to higher dimensions. The term “Euclidean” distinguishes these spaces from the curved space

Curved space

Curved space often refers to a spatial geometry which is not “flat” where a flat space is described by Euclidean geometry. Curved spaces can generally be described by Riemannian geometry though some simple cases can be described in other ways. Curved spaces play an essential role in General...

s of non-Euclidean geometry

Non-Euclidean geometry

Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...

and Einstein's

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

general theory of relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, and is named for the Greek

Greeks

The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....

mathematician Euclid of Alexandria

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

.

Classical Greek geometry defined the Euclidean plane and Euclidean three-dimensional space using certain postulates

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

, while the other properties of these spaces were deduced as theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

s. In modern mathematics, it is more common to define Euclidean space using Cartesian coordinates and the ideas of analytic geometry

Analytic geometry

Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...

. This approach brings the tools of algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

and calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

to bear on questions of geometry, and has the advantage that it generalizes easily to Euclidean spaces of more than three dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

s.

From the modern viewpoint, there is essentially only one Euclidean space of each dimension. In dimension one this is the real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

; in dimension two it is the Cartesian plane; and in higher dimensions it is the real coordinate space

Coordinate space

In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...

with three or more real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

coordinates. Thus a point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

in Euclidean space is a tuple

Tuple

In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

of real numbers, and distances are defined using the Euclidean distance formula

Euclidean distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

. Mathematicians often denote the n-dimensional Euclidean space by

, or sometimes

if they wish to emphasize its Euclidean nature. Euclidean spaces have finite dimension.

Intuitive overview

One way to think of the Euclidean plane is as a set of point

Point (geometry)

s satisfying certain relationships, expressible in terms of distance and angle. For example, there are two fundamental operations on the plane. One is translation

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

, which means a shifting of the plane so that every point is shifted in the same direction and by the same distance. The other is rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

about a fixed point in the plane, in which every point in the plane turns about that fixed point through the same angle. One of the basic tenets of Euclidean geometry is that two figures (that is, subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

s) of the plane should be considered equivalent (congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

) if one can be transformed into the other by some sequence of translations, rotations and reflection

Reflection (mathematics)

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

s. (See Euclidean group

Euclidean group

In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...

.)

In order to make all of this mathematically precise, one must clearly define the notions of distance, angle, translation, and rotation. The standard way to do this, as carried out in the remainder of this article, is to define the Euclidean plane as a two-dimensional real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

equipped with an inner product. For then:

the vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....

s in the vector space correspond to the points of the Euclidean plane,
the addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....

operation in the vector space corresponds to translation, and
the inner product implies notions of angle and distance, which can be used to define rotation.

Once the Euclidean plane has been described in this language, it is actually a simple matter to extend its concept to arbitrary dimensions. For the most part, the vocabulary, formulas, and calculations are not made any more difficult by the presence of more dimensions. (However, rotations are more subtle in high dimensions, and visualizing high-dimensional spaces remains difficult, even for experienced mathematicians.)

A final wrinkle is that Euclidean space is not technically a vector space but rather an affine space

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

, on which a vector space acts

Group action

In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...

. Intuitively, the distinction just says that there is no canonical choice of where the origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

should go in the space, because it can be translated anywhere. In this article, this technicality is largely ignored.

Real coordinate space

Let R denote the field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s. For any positive integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

n, the set of all n-tuple

Tuple

s of real numbers forms an n-dimensional vector space over R, which is denoted Rⁿ and sometimes called real coordinate space. An element of Rⁿ is written

where each x_i is a real number. The vector space operations on Rⁿ are defined by

The vector space Rⁿ comes with a standard basis

Standard basis

In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...

An arbitrary vector in Rⁿ can then be written in the form

Rⁿ is the prototypical example of a real n-dimensional vector space. In fact, every real n-dimensional vector space V is isomorphic to Rⁿ. This isomorphism is not canonical, however. A choice of isomorphism is equivalent to a choice of basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

for V (by looking at the image of the standard basis for Rⁿ in V). The reason for working with arbitrary vector spaces instead of Rⁿ is that it is often preferable to work in a coordinate-free manner (that is, without choosing a preferred basis).

Euclidean structure

Euclidean space is more than just a real coordinate space. In order to apply Euclidean geometry one needs to be able to talk about the distances between points and the angles between lines or vectors. The natural way to obtain these quantities is by introducing and using the standard inner product (also known as the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

) on Rⁿ. The inner product of any two real n-vectors x and y is defined by

The result is always a real number. Furthermore, the inner product of x with itself is always nonnegative. This product allows us to define the "length" of a vector x as

This length function satisfies the required properties of a norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

and is called the Euclidean norm on Rⁿ.

The (non-reflex) angle θ (0° ≤ θ ≤ 180°) between x and y is then given by

where cos⁻¹ is the arccosine function.

Finally, one can use the norm to define a metric

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

(or distance function) on Rⁿ by

This distance function is called the Euclidean metric
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

. It can be viewed as a form of the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

.

Real coordinate space together with this Euclidean structure is called Euclidean space and often denoted Eⁿ. (Many authors refer to Rⁿ itself as Euclidean space, with the Euclidean structure being understood). The Euclidean structure makes Eⁿ an inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

(in fact a Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

), a normed vector space

Normed vector space

In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....

, and a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

.

Rotations of Euclidean space are then defined as orientation

Orientation (mathematics)

In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...

-preserving linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

s T that preserve angles and lengths:

In the language of matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

, rotations are special orthogonal matrices.

Topology of Euclidean space

Since Euclidean space is a metric space

Metric space

it is also a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

with the natural topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

induced by the metric. The metric topology on Eⁿ is called the Euclidean topology. A set is open

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

in the Euclidean topology if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

it contains an open ball around each of its points. The Euclidean topology turns out to be equivalent to the product topology

Product topology

In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...

on Rⁿ considered as a product of n copies of the real line

Real line

R (with its standard topology).

An important result on the topology of Rⁿ, that is far from superficial, is Brouwer's invariance of domain

Invariance of domain

Invariance of domain is a theorem in topology about homeomorphic subsets of Euclidean space Rn. It states:The theorem and its proof are due to L.E.J. Brouwer, published in 1912...

. Any subset of Rⁿ (with its subspace topology

Subspace topology

In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...

) that is homeomorphic to another open subset of Rⁿ is itself open. An immediate consequence of this is that R^m is not homeomorphic to Rⁿ if m ≠ n — an intuitively "obvious" result which is nonetheless difficult to prove.

Generalizations

In modern mathematics, Euclidean spaces form the prototypes for other, more complicated geometric objects. For example, a smooth manifold is a Hausdorff

Hausdorff space

In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...

topological space that is locally diffeomorphic to Euclidean space. Diffeomorphism does not respect distance and angle, so these key concepts of Euclidean geometry are lost on a smooth manifold. However, if one additionally prescribes a smoothly varying inner product on the manifold's tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

s, then the result is what is called a Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

. Put differently, a Riemannian manifold is a space constructed by deforming and patching together Euclidean spaces. Such a space enjoys notions of distance and angle, but they behave in a curved

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

, non-Euclidean manner. The simplest Riemannian manifold, consisting of Rⁿ with a constant inner product, is essentially identical to Euclidean n-space itself.

If one alters a Euclidean space so that its inner product becomes negative in one or more directions, then the result is a pseudo-Euclidean space

Pseudo-Euclidean space

A pseudo-Euclidean space is a finite-dimensional real vector space together with a non-degenerate indefinite quadratic form. Such a quadratic form can, after a change of coordinates, be written as...

. Smooth manifolds built from such spaces are called pseudo-Riemannian manifold

Pseudo-Riemannian manifold

In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...

s. Perhaps their most famous application is the theory of relativity

Theory of relativity

The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....

, where empty spacetime

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

with no matter

Matter

Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...

is represented by the flat pseudo-Euclidean space called Minkowski space

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

, spacetimes with matter in them form other pseudo-Riemannian manifolds, and gravity corresponds to the curvature of such a manifold.

Our universe, being subject to relativity, is not Euclidean. This becomes significant in theoretical considerations of astronomy

Astronomy

Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...

and cosmology

Cosmology

Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...

, and also in some practical problems such as global positioning and airplane navigation

Navigation

Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...

. Nonetheless, a Euclidean model of the universe can still be used to solve many other practical problems with sufficient precision.

Intuitive overview

Real coordinate space

Euclidean structure

Topology of Euclidean space

Generalizations

See also