Minkowski space - AbsoluteAstronomy.com

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

and mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Minkowski space or Minkowski spacetime (named after the mathematician Hermann Minkowski

Hermann Minkowski

Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...

) is the mathematical setting in which Einstein's

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

theory of special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

is most conveniently formulated. In this setting the three ordinary dimensions of space

Space

Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...

are combined with a single dimension of time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

to form a four-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

for representing a spacetime

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

.

In theoretical physics

Theoretical physics

Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...

, Minkowski space is often contrasted with Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. While a Euclidean space has only spacelike dimensions, a Minkowski space also has one timelike dimension. Therefore the symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

of a Euclidean space is the Euclidean group

Euclidean group

In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...

and for a Minkowski space it is the Poincaré group

Poincaré group

In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...

.

The spacetime interval between two events in Minkowski Space is either space-like, light-like ('null') or time-like.

History

In 1905–6 it was noted by Henri Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

that, by taking time to be the imaginary part of the fourth spacetime

Spacetime

coordinate √ c
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

t
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

, the Lorentz transformation

Lorentz transformation

In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...

can be regarded as a rotation in a four-dimensional Euclidean space with three real coordinates representing space, and one imaginary coordinate

Imaginary time

Imaginary time is a concept derived from quantum mechanics and is essential in connecting quantum mechanics with statistical mechanics.- In quantum mechanics :...

, representing time, as the fourth dimension. This idea was elaborated by Hermann Minkowski

Hermann Minkowski

who used it to restate the Maxwell equations in four dimensions showing directly their invariance under Lorentz transformation. He further reformulated in four dimensions the then-recent theory of special relativity of Einstein

Albert Einstein

. From this he concluded that time and space should be treated equally and so arose his concept of events taking place in a unified four-dimensional space-time continuum. In a further development he gave an alternative formulation of this idea which did not use the imaginary time coordinate but represented the four variables (x, y, z, t) of space and time in coordinate form in a four dimensional affine space

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

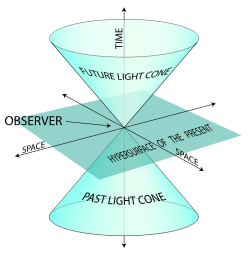
. Points in this space correspond to events in space time. In this space there is defined the light-cone associated with each point (see diagram above) and events not on the light-cone are classified by their relation to the apex as space-like or time-like. It is principally this view of space-time that is current nowadays, although the older view involving imaginary time has also influenced special relativity. Minkowski, aware of the fundamental restatement of the theory which he had made, said:

The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality. – Hermann Minkowski, 1908

For further historical information see references Galison (1979), Corry (1997), Walker (1999)

Structure

Formally, Minkowski space is a four-dimensional real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

equipped with a nondegenerate, symmetric bilinear form with signature

Metric signature

The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...

(−,+,+,+) (Some may also prefer the alternative signature (+,−,−,−); in general, mathematicians and general relativists prefer the former while particle physicists tend to use the latter.) In other words, Minkowski space is a pseudo-Euclidean space

Pseudo-Euclidean space

A pseudo-Euclidean space is a finite-dimensional real vector space together with a non-degenerate indefinite quadratic form. Such a quadratic form can, after a change of coordinates, be written as...

with and (in a broader definition any is allowed). Elements of Minkowski space are called events or four-vector

Four-vector

In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...

s. Minkowski space is often denoted R^1,3 to emphasize the signature, although it is also denoted M⁴ or simply M. It is perhaps the simplest example of a pseudo-Riemannian manifold

Pseudo-Riemannian manifold

In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...

The Minkowski inner product

This inner product is similar to the usual, Euclidean, inner product, but is used to describe a different geometry; the geometry is usually associated with relativity. Let M be a 4-dimensional real vector space. The Minkowski inner product is a map (i.e. given any two vectors v, w in M we define η(v,w) as a real number) which satisfies properties (1), (2), (3) listed here, as well as property (4) given below:

1.	bilinear	η(au+v, w) = aη(u,w) + η(v,w) for all a ∈ R and u, v, w in M.
2	symmetric	η(v,w) = η(w,v) for all v, w ∈ M.
3.	nondegenerate	if η(v,w) = 0 for all w ∈ M then v = 0.

Note that this is not an inner product in the usual sense, since it is not positive-definite

Definite bilinear form

In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...

, i.e. the quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

||v||² = η(v,v) need not be positive. The positive-definite condition has been replaced by the weaker condition of nondegeneracy (every positive-definite form is nondegenerate but not vice-versa). The inner product is said to be indefinite. These misnomer

Misnomer

A misnomer is a term which suggests an interpretation that is known to be untrue. Such incorrect terms sometimes derive their names because of the form, action, or origin of the subject becoming named popularly or widely referenced—long before their true natures were known.- Sources of misnomers...

s, "Minkowski inner product" and "Minkowski metric" conflict with the standard meanings of inner product and metric

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

in pure mathematics; as with many other misnomers the usage of these terms is due to similarity to the mathematical structure.

Just as in Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, two vectors v and w are said to be orthogonal if η(v,w) = 0. But Minkowski space differs by including hyperbolic-orthogonal

Hyperbolic-orthogonal

In plane geometry, two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola.Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.Two particular hyperbolas are frequently used in the plane: x y = 1 ...

events in case v and w span a plane where η takes negative values. This difference is clarified by comparing the Euclidean structure of the ordinary complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

plane to the structure of the plane of split-complex number

Split-complex number

In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...

s. The Minkowski norm of a vector v is defined by

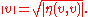
This is not a norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

in the usual sense (it fails to be subadditive), but it does define a useful generalization of the notion of length to Minkowski space. In particular, a vector v is called a unit vector if ||v|| = 1 (i.e.). A basis for M consisting of mutually orthogonal unit vectors is called an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

.

By the Gram–Schmidt process, any inner product space satisfying conditions 1 to 3 above always has an orthonormal basis. Furthermore, the number of positive and negative unit vectors in any such basis is a fixed pair of numbers, equal to the signature of the inner product. This is Sylvester's law of inertia

Sylvester's law of inertia

Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...

.

Then the fourth condition on η can be stated:

4. signature The bilinear form η has signature (−,+,+,+) or (+,−,−,−).

Which signature is used is a matter of convention. Both are fairly common. See sign convention

Sign convention

In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...

Standard basis

A standard basis for Minkowski space is a set of four mutually orthogonal vectors {e₀,e₁,e₂,e₃} such that

−(e₀)² = (e₁)² = (e₂)² = (e₃)² = 1

These conditions can be written compactly in the following form:

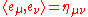
where μ and ν run over the values (0, 1, 2, 3) and the matrix η is given by

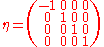
This tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

is frequently called the "Minkowski tensor". Relative to a standard basis, the components of a vector v are written (v⁰,v¹,v²,v³) and we use the Einstein notation

Einstein notation

In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...

to write v = v^μe_μ. The component v⁰ is called the timelike component of v while the other three components are called the spatial components.

In terms of components, the inner product between two vectors v and w is given by

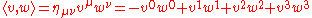
and the norm-squared of a vector v is

v² = η_μν v^μv^ν = −(v⁰)² + (v¹)² + (v²)² + (v³)²

Alternative definition

The section above defines Minkowski space as a vector space

Vector space

. There is an alternative definition of Minkowski space as an affine space

Affine space

which views Minkowski space as a homogeneous space

Homogeneous space

In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...

of the Poincaré group

Poincaré group

In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...

with the Lorentz group

Lorentz group

In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...

as the stabilizer

Group action

In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...

. See Erlangen program

Erlangen program

An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...

.

Note also that the term "Minkowski space" is also used for analogues in any dimension: if n≥2, n-dimensional Minkowski space is a vector space or affine space of real dimension n on which there is an inner product or pseudo-Riemannian metric of signature (n−1,1), i.e., in the above terminology, n−1 "pluses" and one "minus".

Lorentz transformations

All four-vector

Four-vector

s, that is, vectors in Minkowski space, transform in the same manner. In the standard sets of inertial frames as shown by the graph,

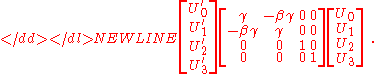
where

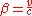
and

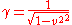
Symmetries

One of the symmetries of Minkowski space is called a "Lorentz boost". This symmetry is often illustrated with a Minkowski diagram

Minkowski diagram

The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...

.

The Poincaré group

Poincaré group

In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...

is the group of isometries of Minkowski spacetime.

Causal structure

Vectors are classified according to the sign of η(v,v). When the standard signature (−,+,+,+) is used, a vector v is:

Timelike	if η(v,v) < 0
Spacelike	if η(v,v) > 0
Null (or lightlike)	if η(v,v) = 0

This terminology comes from the use of Minkowski space in the theory of relativity

Theory of relativity

The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....

. The set of all null vectors at an event of Minkowski space constitutes the light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

of that event. Note that all these notions are independent of the frame of reference. Given a timelike vector v, there is a worldline of constant velocity associated with it. The set {w : η(w,v) = 0 } corresponds to the simultaneous hyperplane at the origin of this worldline. Minkowski space exhibits relativity of simultaneity

Relativity of simultaneity

In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...

since this hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

depends on v. In the plane spanned by v and such a w in the hyperplane, the relation of w to v is hyperbolic-orthogonal

Hyperbolic-orthogonal

.

Once a direction of time is chosen, timelike and null vectors can be further decomposed into various classes. For timelike vectors we have

future directed timelike vectors whose first component is positive, and
past directed timelike vectors whose first component is negative.

Null vectors fall into three classes:

the zero vector, whose components in any basis are (0,0,0,0),
future directed null vectors whose first component is positive, and
past directed null vectors whose first component is negative.

Together with spacelike vectors there are 6 classes in all.

An orthonormal basis for Minkowski space necessarily consists of one timelike and three spacelike unit vectors. If one wishes to work with non-orthonormal bases it is possible to have other combinations of vectors. For example, one can easily construct a (non-orthonormal) basis consisting entirely of null vectors, called a null basis. Over the reals, if two null vectors are orthogonal (zero inner product), then they must be proportional. However, allowing complex numbers, one can obtain a null tetrad which is a basis consisting of null vectors, some of which are orthogonal to each other.

Vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s are called timelike, spacelike or null if the associated vectors are timelike, spacelike or null at each point where the field is defined.

Causality relations

Let x, y ∈ M. We say that

x chronologically precedes y if y − x is future directed timelike.
x causally precedes y if y − x is future directed null

Reversed triangle inequality

If v and w are two equally directed timelike four-vectors, then

where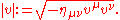

Locally flat spacetime

Strictly speaking, the use of the Minkowski space to describe physical systems over finite distances applies only in the Newtonian limit

Newtonian limit

In physics, the Newtonian limit refers to physical systems without significantly intense gravitation, in the sense that Newton's law of universal gravitation may be used to obtain values that are correct to a high order...

of systems without significant gravitation

Gravitation

Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...

. In the case of significant gravitation, spacetime becomes curved and one must abandon special relativity

Special relativity

in favor of the full theory of general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

.

Nevertheless, even in such cases, Minkowski space is still a good description in an infinitesimally small region

Local reference frame

In theoretical physics, a local reference frame refers to a coordinate system or frame of reference that is only expected to function over a small region or a restricted region of space or spacetime....

surrounding any point (barring gravitational singularities). More abstractly, we say that in the presence of gravity spacetime is described by a curved 4-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

for which the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

to any point is a 4-dimensional Minkowski space. Thus, the structure of Minkowski space is still essential in the description of general relativity.

In the realm of weak gravity, spacetime

Spacetime

becomes flat and looks globally, not just locally, like Minkowski space. For this reason Minkowski space is often referred to as flat spacetime.

External links

Animation clip visualizing Minkowski space in the context of special relativity.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History

Structure

The Minkowski inner product

Standard basis

Alternative definition

Lorentz transformations

Symmetries

Causal structure

Causality relations

Reversed triangle inequality

Locally flat spacetime

See also

External links