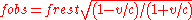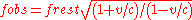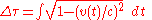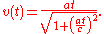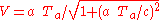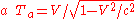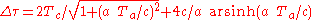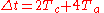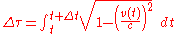
Twin paradox
Encyclopedia
In physics, the twin paradox is a thought experiment
in special relativity
, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth. This result appears puzzling because each twin sees the other twin as traveling, and so, according to a naive application of time dilation
, each should paradoxically
find the other to have aged more slowly. In fact, the result is not a paradox
in the true sense, since it can be resolved within the standard framework of special relativity. The effect has been verified experimentally using measurements of cesium beam atomic clocks
flown in airplanes and satellites.
Starting with Paul Langevin
in 1911, there have been numerous explanations of this paradox, many based upon there being no contradiction because there is no symmetry—only one twin has undergone acceleration and deceleration, thus differentiating the two cases. One version of the asymmetry argument made by Max von Laue
in 1913 is that the traveling twin uses two inertial frames
: one on the way up and the other on the way down. So switching frames is the cause of the difference, not acceleration per se.
Other explanations account for the effects of acceleration. Einstein
, Born
and Møller invoked gravitational time dilation
to explain the aging on the basis of the effects of acceleration. Both gravitational time dilation and special relativity can be used to explain the Hafele-Keating experiment
on time dilation using precise measurements of clocks flown in airplanes.
In his famous work on special relativity
in 1905, Albert Einstein
predicted that when two clock
s were brought together and synchronized, and then one was moved away and brought back, the clock which had undergone the traveling would be found to be lagging behind the clock which had stayed put. Einstein considered this to be a natural consequence of special relativity, not a paradox
as some suggested, and in 1911, he restated and elaborated on this result as printed below, (with physicist Robert Resnick
's comments following Einstein's):
In 1911, Paul Langevin
gave a "striking example" by describing the story of a traveler making a trip at a Lorentz factor
of
. The traveler remains in a projectile for one year of his time, and then reverses direction. Upon return, the traveler will find that he has aged two years, while 200 years have passed on Earth. During the trip, both the traveler and Earth keep sending signals to each other at a constant rate, which places Langevin's story among the Doppler shift versions of the twin paradox. The relativistic effects upon the signal rates are used to account for the different aging rates. The asymmetry that occurred because only the traveler underwent acceleration, is used to explain why there is any difference at all, because "any change of velocity, or any acceleration has an absolute meaning".
Max von Laue
(1911, 1913) elaborated on Langevin's explanation. Using Minkowski's spacetime
formalism, Laue went on to demonstrate that the world line
s of the inertially moving bodies maximize the proper time
elapsed between two events. He also wrote that the asymmetric aging is completely accounted for by the fact that the astronaut twin travels in two separate frames, while the earth twin remains in one frame, and the time of acceleration can be made arbitrarily small compared with the time of inertial motion.
Eventually, Lord Halsbury and others removed any acceleration by introducing the "three-brother" approach. The traveling twin transfers his clock reading to a third one, traveling in the opposite direction. Another way of avoiding acceleration effects is the use of the relativistic Doppler effect.
Neither Einstein nor Langevin considered such results to be literally paradoxical: Einstein only called it "peculiar" while Langevin presented it as a consequence of absolute acceleration."We are going to see this absolute character of the acceleration manifest itself in another form." ("Nous allons voir se manifester sous une autre forme ce caractère absolu de l’accélération."), page 82 of Langevin1911 A paradox in logical and scientific usage refers to results which are inherently contradictory, that is, logically impossible and both men argued that, from the time differential illustrated by the story of the twins, no self-contradiction could be constructed. In other words, neither Einstein nor Langevin saw the story of the twins as constituting a challenge to the self-consistency of relativistic physics.
light years away, at a speed 
(i.e., 80 percent of the speed of light).
(To make the numbers easy, the ship is assumed to attain its full speed immediately upon departure - actually it would need more than a year accelerating at 1 G to get up to speed.)
The Earth-based mission control reasons about the journey this way : the round trip will take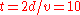
years in Earth time (i.e. everybody on earth will be 10 years older when the ship returns). The amount of time as measured on the ship's clocks and the aging of the travelers during their trip will be reduced by the factor 
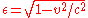, the reciprocal of the Lorentz factor
. In this case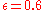
and the travelers will have aged only 0.600×10 = 6 years when they return.
The ship's crew members also calculate the particulars of their trip from their perspective. They know that the distant star system and the Earth are moving relative to the ship at speed
during the trip. In their rest frame the distance between the Earth and the star system is 
= 2.4 light years (length contraction
), for both the outward and return journeys. Each half of the journey takes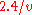
= 3 years, and the round trip takes 2×3 = 6 years. Their calculations show that they will arrive home having aged 6 years. The travelers' final calculation is in complete agreement with the calculations of those on Earth, though they experience the trip quite differently from those who stay at home.
If a pair of twins are born on the day the ship leaves, and one goes on the journey while the other stays on Earth, they will meet again when the traveler is 6 years old and the stay-at-home twin is 10 years old. The calculation illustrates the usage of the phenomenon of length contraction
and the experimentally verified phenomenon of time dilation
to describe and calculate consequences and predictions of Einstein's special theory of relativity.
Special relativity does not claim that all observers are equivalent, only that all observers at rest in inertial reference frames are equivalent. But the space ship jumps frames (accelerates) when it performs a U-turn. In contrast, the twin who stays home remains in the same inertial frame for the whole duration of his brother's flight. No accelerating or decelerating forces apply to the homebound twin.
There are indeed not two but three relevant inertial frames: the one in which the stay-at-home twin remains at rest, the one in which the traveling twin is at rest on his outward trip, and the one in which he is at rest on his way home. It is during the acceleration at the U-turn that the traveling twin switches frames. That is when he must adjust his calculated age of the twin at rest.
In special relativity there is no concept of absolute present. A present is defined as a set of events that are simultaneous from the point of view of a given observer. The notion of simultaneity depends on the frame of reference (see relativity of simultaneity
), so switching between frames requires an adjustment in the definition of the present. If one imagines a present as a (three-dimensional) simultaneity plane in Minkowski space
, then switching frames results in changing the inclination of the plane.
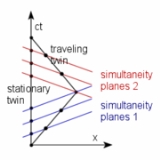
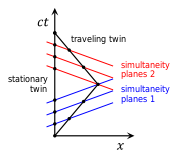In the spacetime diagram on the right, drawn for the reference frame of the stay-at-home twin, that twin's world line coincides with the vertical axis (his position is constant in space, moving only in time). On the first leg of the trip, the second twin moves to the right (black sloped line); and on the second leg, back to the left. Blue lines show the planes of simultaneity for the traveling twin during the first leg of the journey; red lines, during the second leg. Just before turnaround, the traveling twin calculates the age of the resting twin by measuring the interval along the vertical axis from the origin to the upper blue line. Just after turnaround, if he recalculates, he'll measure the interval from the origin to the lower red line. In a sense, during the U-turn the plane of simultaneity jumps from blue to red and very quickly sweeps over a large segment of the world line of the resting twin. The traveling twin reckons that there has been a jump discontinuity in the age of the resting twin.
The twin paradox illustrates a feature of the special relativistic spacetime
model, the Minkowski space
. The world line
s of the inertially moving bodies are the geodesics of Minkowskian spacetime. In Minkowski geometry the world lines of inertially moving bodies maximize the proper time
elapsed between two events.
considerations, as seen in Einstein's original paper on the subject, as well as in all subsequent derivations of the Lorentz transformations.
Because spacetime diagrams incorporate Einstein's clock synchronization, there will be a requisite "jump in time" in the calculation made by a "suddenly returning astronaut" who inherits a "new meaning of simultaneity" in keeping with that clock synchronization (with its lattice of clocks methodology) as explained in Spacetime Physics by John A. Wheeler. Such clock synchronization makes an absolute frame of reference superfluous for all predictive purposes.
If, instead of incorporating Einstein's clock synchronization (lattice of clocks), the astronaut (outgoing and incoming) and the earth-bound party regularly update each other on the status of their clocks by way of sending radio signals (which travel at light speed), then all parties will note an incremental build up of asymmetry in time-keeping, beginning at the "turn around" point. Prior to the "turn around", each party regards the other party's clock to be recording time differently than his own, but the noted difference is symmetrical between the two parties. After the "turn around", the noted differences are not symmetrical, and the asymmetry grows incrementally until the two parties are reunited. Upon finally reuniting, this asymmetry can be seen in the actual difference showing on the two reunited clocks.
Shortly after departure, the traveling twin sees the stay-at-home twin with no time delay. At arrival, the image in the ship screen shows the staying twin as he was 1 year after launch, because radio emitted from Earth 1 year after launch gets to the other star 4 years afterwards and meets the ship there. During this leg of the trip, the traveling twin sees his own clock advance 3 years and the clock in the screen advance 1 year, so it seems to advance at 1/3 the normal rate, just 20 image seconds per ship minute. This combines the effects of time dilation due to motion (by factor ε=0.6, five years on earth are 3 years on ship) and the effect of increasing light-time-delay (which grows from 0 to 4 years).
Of course, the observed frequency of the transmission is also 1/3 the frequency of the transmitter (a reduction in frequency; "red-shifted"). This is called the relativistic Doppler effect
. The frequency of clock-ticks (or of wavefronts) which one sees from a source with rest frequency
is
when the source is moving directly away. This is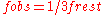
for v/c=0.8.
As for the stay-at-home twin, he gets a slowed signal from the ship for 9 years, at a frequency 1/3 the transmitter frequency. During these 9 years, the clock of the traveling twin in the screen seem to advance 3 years, so both twins see the image of their sibling aging at a rate only 1/3 their own rate. Expressed in other way, they would both see the other's clock run at 1/3 their own clock speed. If they factor out of the calculation the fact that the light-time delay of the transmission is increasing at a rate of 0.8 seconds per second, BOTH can work out that the other twin is aging slower, at 60% rate.
Then the ship turns back toward home. The clock of the staying twin shows ' 1 year after launch' in the screen of the ship, and during the 3 years of the trip back it increases up to '10 years after launch', so the clock in the screen seems to be advancing 3 times faster than usual.
When the source is moving towards the observer, the observed frequency is higher ("blue-shifted") and given by
This is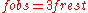
for v/c=0.8.
As for the screen on earth, it shows that trip back beginning 9 years after launch, and the traveling clock in the screen shows that 3 years have passed on the ship. One year later, the ship is back home and the clock shows 6 years. So, during the trip back, BOTH twins see their sibling's clock going 3 times faster than their own. Factoring out the fact that the light-time-delay is decreasing by 0.8 seconds every second, each twin calculates that the other twin is aging at 60% his own aging speed.
The 
(space-time) diagrams at left show the paths of light signals traveling between Earth and ship (1st diagram) and between ship and Earth (2nd diagram). These signals carry the images of each twin and his age-clock to the other twin. The vertical black line is the Earth's path through space time and the other two sides of the triangle show the ship's path through space time (as in the Minkowski diagram above). As far as the sender is concerned, he transmits these at equal intervals (say, once an hour) according to his own clock; but according to the clock of the twin receiving these signals, they are not being received at equal intervals.
After the ship has reached its cruising speed of 0.8 c, each twin would see 1 second pass in the received image of the other twin for every 3 seconds of his own time. That is, each would see the image of the other's clock going slow, not just slow by the ε factor 0.6, but even slower because light-time-delay is increasing 0.8 seconds per second. This is shown in the figures by red light paths. At some point, the images received by each twin change so that each would see 3 seconds pass in the image for every second of his own time. That is, the received signal has been increased in frequency by the Doppler shift. These high frequency images are shown in the figures by blue light paths.
that more blue-shifted (fast aging) images are received by the Ship. Put another way, the space ship sees the image change from a red-shift (slower aging of the image) to a blue-shift (faster aging of the image) at the mid-point of its trip (at the turnaround, 5 years after departure); the Earth sees the image of the ship change from red-shift to blue shift after 9 years (almost at the end of the period that the ship is absent). In the next section, one will see another asymmetry in the images: the Earth twin sees the ship twin age by the same amount in the red and blue shifted images; the ship twin sees the Earth twin age by different amounts in the red and blue shifted images.
The Earth twin sees 9 years of slow (red) images of the ship twin, during which the ship twin ages (in the image) by 9/3 = 3 years. He then sees fast (blue) images for the remaining 1 year until the ship returns. In the fast images, the ship twin ages by 1 × 3 = 3 years. The total aging of the ship twin in the images received by Earth is 3 + 3 = 6 years, so the ship twin returns younger (6 years as opposed to 10 years on Earth).
when the image was emitted. A similar calculation reveals that his twin was aging at the same reduced rate of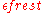
in all low frequency images.
, the traveling twin may analyze the turnaround phase as if the stay-at-home twin were freely falling in a gravitational field and as if the traveling twin were stationary. A 1918 paper by Einstein presents a conceptual sketch of the idea.Einstein, A. (1918) "dialog about objections against the theory of relativity", Die Naturwissenschaften 48, pp. 697-702, 29 November 1918 From the viewpoint of the traveler, a calculation for each separate leg, ignoring the turnaround, leads to a result in which the Earth clocks age less than the traveler. For example, if the Earth clocks age 1 day less on each leg, the amount that the Earth clocks will lag behind amounts to 2 days. The physical description of what happens at turnaround has to produce a contrary effect of double that amount: 4 days' advancing of the Earth clocks. Then the traveler's clock will end up with a net 2-day delay on the Earth clocks, in agreement with calculations done in the frame of the stay-at-home twin.
The mechanism for the advancing of the stay-at-home twin's clock is gravitational time dilation
. When an observer finds that inertially moving objects are being accelerated with respect to themselves, those objects are in a gravitational field insofar as relativity is concerned. For the traveling twin at turnaround, this gravitational field fills the universe. In a weak field approximation, clocks tick at a rate of
where 
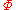is the difference in gravitational potential. In this case, 
where g is the acceleration of the traveling observer during turnaround and h is the distance to the stay-at-home twin. The rocket is firing towards the stay-at-home twin, thereby placing that twin at a higher gravitational potential. Due to the large distance between the twins, the stay-at-home twin's clocks will appear to be sped up enough to account for the difference in proper times experienced by the twins. It is no accident that this speed-up is enough to account for the simultaneity shift described above. The general relativity solution for a static homogeneous gravitational field and the special relativity solution for finite acceleration produce identical results.
Other calculations have been done for the traveling twin (or for any observer who sometimes accelerates), which do not involve the equivalence principle, and which do not involve any gravitational fields. Such calculations are based only on the special theory, not the general theory, of relativity. One
approach calculates surfaces of simultaneity by considering light pulses, in accordance with Hermann Bondi
's idea of the k-calculus. A second approach calculates a straightforward but technically complicated integral to determine how the traveling twin measures the elapsed time on the stay-at-home clock. An outline of this second approach is given in a separate section below.
Let clock K be associated with the "stay at home twin".
Let clock K' be associated with the rocket that makes the trip.
At the departure event both clocks are set to 0.
Knowing that the clock K remains inertial (stationary), the total accumulated proper time
of clock K' will be given by the integral function of coordinate time
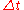
where v(t) is the coordinate velocity of clock K' as a function of t according to clock K, and, e.g. during phase 1, given by
This integral can be calculated for the 6 phases:
where a is the proper acceleration, felt by clock K' during the acceleration phase(s) and where the following relations hold between V, a and Ta:
So the traveling clock K' will show an elapsed time of
which can be expressed as
whereas the stationary clock K shows an elapsed time of
which is, for every possible value of a, Ta, Tc and V, larger than the reading of clock K':
(here
is another customary notation for the time of the non-inertial observer 
) gives us the dependence of the proper time 
on the time elapsed in the inertial frame 
, assumed the velocity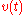 
is known. Actually, this equation answers the problem of the dependence between proper time and inertial time for the inertial observer at rest in 
but not for the moving observer. Indeed, the data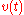 
is not always easily accessible from the ship. The observer in the non-inertial frame 
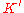may find it difficult to measure its velocity with respect to 
, not to mention that this velocity has to be parametrized with respect to the inertial time of 
, a step which needs the dependence between proper and inertial time to be known in advance. Can the non-inertial observer predict what will be the time elapsed for the twin which remained at home using only easily accessible data? The answer is affirmative and at least for a unidirectional motion has a simple answer given by
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth. This result appears puzzling because each twin sees the other twin as traveling, and so, according to a naive application of time dilation
Time dilation
In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
, each should paradoxically
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
find the other to have aged more slowly. In fact, the result is not a paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
in the true sense, since it can be resolved within the standard framework of special relativity. The effect has been verified experimentally using measurements of cesium beam atomic clocks
Atomic clock
An atomic clock is a clock that uses an electronic transition frequency in the microwave, optical, or ultraviolet region of the electromagnetic spectrum of atoms as a frequency standard for its timekeeping element...
flown in airplanes and satellites.
Starting with Paul Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
in 1911, there have been numerous explanations of this paradox, many based upon there being no contradiction because there is no symmetry—only one twin has undergone acceleration and deceleration, thus differentiating the two cases. One version of the asymmetry argument made by Max von Laue
Max von Laue
Max Theodor Felix von Laue was a German physicist who won the Nobel Prize in Physics in 1914 for his discovery of the diffraction of X-rays by crystals...
in 1913 is that the traveling twin uses two inertial frames
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
: one on the way up and the other on the way down. So switching frames is the cause of the difference, not acceleration per se.
Other explanations account for the effects of acceleration. Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
and Møller invoked gravitational time dilation
Gravitational time dilation
Gravitational time dilation is the effect of time passing at different rates in regions of different gravitational potential; the lower the gravitational potential, the more slowly time passes...
to explain the aging on the basis of the effects of acceleration. Both gravitational time dilation and special relativity can be used to explain the Hafele-Keating experiment
Hafele-Keating experiment
The Hafele–Keating experiment was a test of the theory of relativity. In October 1971, Joseph C. Hafele, a physicist, and Richard E. Keating, an astronomer, took four cesium-beam atomic clocks aboard commercial airliners and flew twice around the world, first eastward, then westward, and compared...
on time dilation using precise measurements of clocks flown in airplanes.
History
- Further information: Time dilation and twin paradox
In his famous work on special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
in 1905, Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
predicted that when two clock
Clock
A clock is an instrument used to indicate, keep, and co-ordinate time. The word clock is derived ultimately from the Celtic words clagan and clocca meaning "bell". A silent instrument missing such a mechanism has traditionally been known as a timepiece...
s were brought together and synchronized, and then one was moved away and brought back, the clock which had undergone the traveling would be found to be lagging behind the clock which had stayed put. Einstein considered this to be a natural consequence of special relativity, not a paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
as some suggested, and in 1911, he restated and elaborated on this result as printed below, (with physicist Robert Resnick
Robert Resnick
Robert Resnick is a well-respected physics educator and author of physics textbooks.He was born in Baltimore, Maryland on January 11, 1923 and graduated from the Baltimore City College high school in 1939. He received his B.A. in 1943 and his Ph.D. in 1949, both in physics from Johns Hopkins...
's comments following Einstein's):
"If we placed a living organism in a box ... one could arrange that the organism, after any arbitrary lengthy flight, could be returned to its original spot in a scarcely altered condition, while corresponding organisms which had remained in their original positions had already long since given way to new generations. For the moving organism, the lengthy time of the journey was a mere instant, provided the motion took place with approximately the speed of light."
If the stationary organism is a man and the traveling one is his twin, then the traveler returns home to find his twin brother much aged compared to himself. The paradox centers around the contention that, in relativity, either twin could regard the other as the traveler, in which case each should find the other younger—a logical contradiction. This contention assumes that the twins' situations are symmetrical and interchangeable, an assumption that is not correct. Furthermore, the accessible experiments have been done and support Einstein's prediction. ...
In 1911, Paul Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
gave a "striking example" by describing the story of a traveler making a trip at a Lorentz factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
of
. The traveler remains in a projectile for one year of his time, and then reverses direction. Upon return, the traveler will find that he has aged two years, while 200 years have passed on Earth. During the trip, both the traveler and Earth keep sending signals to each other at a constant rate, which places Langevin's story among the Doppler shift versions of the twin paradox. The relativistic effects upon the signal rates are used to account for the different aging rates. The asymmetry that occurred because only the traveler underwent acceleration, is used to explain why there is any difference at all, because "any change of velocity, or any acceleration has an absolute meaning".Max von Laue
Max von Laue
Max Theodor Felix von Laue was a German physicist who won the Nobel Prize in Physics in 1914 for his discovery of the diffraction of X-rays by crystals...
(1911, 1913) elaborated on Langevin's explanation. Using Minkowski's spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
formalism, Laue went on to demonstrate that the world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s of the inertially moving bodies maximize the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
elapsed between two events. He also wrote that the asymmetric aging is completely accounted for by the fact that the astronaut twin travels in two separate frames, while the earth twin remains in one frame, and the time of acceleration can be made arbitrarily small compared with the time of inertial motion.
Eventually, Lord Halsbury and others removed any acceleration by introducing the "three-brother" approach. The traveling twin transfers his clock reading to a third one, traveling in the opposite direction. Another way of avoiding acceleration effects is the use of the relativistic Doppler effect.
Neither Einstein nor Langevin considered such results to be literally paradoxical: Einstein only called it "peculiar" while Langevin presented it as a consequence of absolute acceleration."We are going to see this absolute character of the acceleration manifest itself in another form." ("Nous allons voir se manifester sous une autre forme ce caractère absolu de l’accélération."), page 82 of Langevin1911 A paradox in logical and scientific usage refers to results which are inherently contradictory, that is, logically impossible and both men argued that, from the time differential illustrated by the story of the twins, no self-contradiction could be constructed. In other words, neither Einstein nor Langevin saw the story of the twins as constituting a challenge to the self-consistency of relativistic physics.
Specific example
Consider a space ship traveling from Earth to the nearest star system outside of our solar system: a distance light years away, at a speed (i.e., 80 percent of the speed of light).(To make the numbers easy, the ship is assumed to attain its full speed immediately upon departure - actually it would need more than a year accelerating at 1 G to get up to speed.)
The Earth-based mission control reasons about the journey this way : the round trip will take
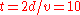years in Earth time (i.e. everybody on earth will be 10 years older when the ship returns). The amount of time as measured on the ship's clocks and the aging of the travelers during their trip will be reduced by the factor 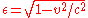, the reciprocal of the Lorentz factorLorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
. In this case
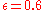and the travelers will have aged only 0.600×10 = 6 years when they return.The ship's crew members also calculate the particulars of their trip from their perspective. They know that the distant star system and the Earth are moving relative to the ship at speed
during the trip. In their rest frame the distance between the Earth and the star system is = 2.4 light years (length contractionLength contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
), for both the outward and return journeys. Each half of the journey takes
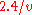= 3 years, and the round trip takes 2×3 = 6 years. Their calculations show that they will arrive home having aged 6 years. The travelers' final calculation is in complete agreement with the calculations of those on Earth, though they experience the trip quite differently from those who stay at home.If a pair of twins are born on the day the ship leaves, and one goes on the journey while the other stays on Earth, they will meet again when the traveler is 6 years old and the stay-at-home twin is 10 years old. The calculation illustrates the usage of the phenomenon of length contraction
Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
and the experimentally verified phenomenon of time dilation
Time dilation
In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
to describe and calculate consequences and predictions of Einstein's special theory of relativity.
Resolution of the paradox in special relativity
The standard textbook approach treats the twin paradox as a straightforward application of special relativity. Here the Earth and the ship are not in a symmetrical relationship: the ship has a turnaround in which it undergoes non-inertial motion, while the Earth has no such turnaround. Since there is no symmetry, it is not paradoxical if one twin is younger than the other. Nevertheless it is still useful to show that special relativity is self-consistent, and how the calculation is done from the standpoint of the traveling twin.Special relativity does not claim that all observers are equivalent, only that all observers at rest in inertial reference frames are equivalent. But the space ship jumps frames (accelerates) when it performs a U-turn. In contrast, the twin who stays home remains in the same inertial frame for the whole duration of his brother's flight. No accelerating or decelerating forces apply to the homebound twin.
There are indeed not two but three relevant inertial frames: the one in which the stay-at-home twin remains at rest, the one in which the traveling twin is at rest on his outward trip, and the one in which he is at rest on his way home. It is during the acceleration at the U-turn that the traveling twin switches frames. That is when he must adjust his calculated age of the twin at rest.
In special relativity there is no concept of absolute present. A present is defined as a set of events that are simultaneous from the point of view of a given observer. The notion of simultaneity depends on the frame of reference (see relativity of simultaneity
Relativity of simultaneity
In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
), so switching between frames requires an adjustment in the definition of the present. If one imagines a present as a (three-dimensional) simultaneity plane in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, then switching frames results in changing the inclination of the plane.
The twin paradox illustrates a feature of the special relativistic spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
model, the Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. The world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s of the inertially moving bodies are the geodesics of Minkowskian spacetime. In Minkowski geometry the world lines of inertially moving bodies maximize the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
elapsed between two events.
Transfer of clock reading in a twin paradox trip
An "out and back" twin paradox adventure may incorporate the transfer of clock reading from an "outgoing" astronaut to an "incoming" astronaut, thus entirely eliminating the effect of acceleration. Acceleration is not involved in any kinematical effects of special relativity. The time differential between two reunited clocks is deduced through purely uniform linear motionLinear motion
Linear motion is motion along a straight line, and can therefore be described mathematically using only one spatial dimension. The linear motion can be of two types: uniform linear motion, with constant velocity or zero acceleration; non uniform linear motion, with variable velocity or non-zero...
considerations, as seen in Einstein's original paper on the subject, as well as in all subsequent derivations of the Lorentz transformations.
Because spacetime diagrams incorporate Einstein's clock synchronization, there will be a requisite "jump in time" in the calculation made by a "suddenly returning astronaut" who inherits a "new meaning of simultaneity" in keeping with that clock synchronization (with its lattice of clocks methodology) as explained in Spacetime Physics by John A. Wheeler. Such clock synchronization makes an absolute frame of reference superfluous for all predictive purposes.
If, instead of incorporating Einstein's clock synchronization (lattice of clocks), the astronaut (outgoing and incoming) and the earth-bound party regularly update each other on the status of their clocks by way of sending radio signals (which travel at light speed), then all parties will note an incremental build up of asymmetry in time-keeping, beginning at the "turn around" point. Prior to the "turn around", each party regards the other party's clock to be recording time differently than his own, but the noted difference is symmetrical between the two parties. After the "turn around", the noted differences are not symmetrical, and the asymmetry grows incrementally until the two parties are reunited. Upon finally reuniting, this asymmetry can be seen in the actual difference showing on the two reunited clocks.
The equivalence of biological aging and clock time-keeping
It would probably be prudent to mention: All processes—chemical, biological, measuring apparatus functioning, human perception involving the eye and brain, the communication of force—everything, is constrained by the speed of light. There is clock functioning at every level, dependent on light speed and the inherent delay at even the atomic level. Thus, we speak of the "twin paradox", involving biological aging. It is in no way different from clock time-keeping. Biological aging is equated to clock time-keeping by John A. Wheeler in Spacetime Physics.What it looks like: the relativistic Doppler shift
Now, if both twins send a video feed of themselves to each other, what do they see in their screens? Or, if each twin always carried a clock indicating his age, what time would each see in the image of their distant twin and his clock?Shortly after departure, the traveling twin sees the stay-at-home twin with no time delay. At arrival, the image in the ship screen shows the staying twin as he was 1 year after launch, because radio emitted from Earth 1 year after launch gets to the other star 4 years afterwards and meets the ship there. During this leg of the trip, the traveling twin sees his own clock advance 3 years and the clock in the screen advance 1 year, so it seems to advance at 1/3 the normal rate, just 20 image seconds per ship minute. This combines the effects of time dilation due to motion (by factor ε=0.6, five years on earth are 3 years on ship) and the effect of increasing light-time-delay (which grows from 0 to 4 years).
Of course, the observed frequency of the transmission is also 1/3 the frequency of the transmitter (a reduction in frequency; "red-shifted"). This is called the relativistic Doppler effect
Relativistic Doppler effect
The relativistic Doppler effect is the change in frequency of light, caused by the relative motion of the source and the observer , when taking into account effects described by the special theory of relativity.The relativistic Doppler effect is different from the non-relativistic Doppler effect...
. The frequency of clock-ticks (or of wavefronts) which one sees from a source with rest frequency
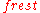is
when the source is moving directly away. This is
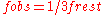for v/c=0.8.As for the stay-at-home twin, he gets a slowed signal from the ship for 9 years, at a frequency 1/3 the transmitter frequency. During these 9 years, the clock of the traveling twin in the screen seem to advance 3 years, so both twins see the image of their sibling aging at a rate only 1/3 their own rate. Expressed in other way, they would both see the other's clock run at 1/3 their own clock speed. If they factor out of the calculation the fact that the light-time delay of the transmission is increasing at a rate of 0.8 seconds per second, BOTH can work out that the other twin is aging slower, at 60% rate.
Then the ship turns back toward home. The clock of the staying twin shows ' 1 year after launch' in the screen of the ship, and during the 3 years of the trip back it increases up to '10 years after launch', so the clock in the screen seems to be advancing 3 times faster than usual.
When the source is moving towards the observer, the observed frequency is higher ("blue-shifted") and given by
This is
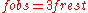for v/c=0.8.As for the screen on earth, it shows that trip back beginning 9 years after launch, and the traveling clock in the screen shows that 3 years have passed on the ship. One year later, the ship is back home and the clock shows 6 years. So, during the trip back, BOTH twins see their sibling's clock going 3 times faster than their own. Factoring out the fact that the light-time-delay is decreasing by 0.8 seconds every second, each twin calculates that the other twin is aging at 60% his own aging speed.
(space-time) diagrams at left show the paths of light signals traveling between Earth and ship (1st diagram) and between ship and Earth (2nd diagram). These signals carry the images of each twin and his age-clock to the other twin. The vertical black line is the Earth's path through space time and the other two sides of the triangle show the ship's path through space time (as in the Minkowski diagram above). As far as the sender is concerned, he transmits these at equal intervals (say, once an hour) according to his own clock; but according to the clock of the twin receiving these signals, they are not being received at equal intervals.After the ship has reached its cruising speed of 0.8 c, each twin would see 1 second pass in the received image of the other twin for every 3 seconds of his own time. That is, each would see the image of the other's clock going slow, not just slow by the ε factor 0.6, but even slower because light-time-delay is increasing 0.8 seconds per second. This is shown in the figures by red light paths. At some point, the images received by each twin change so that each would see 3 seconds pass in the image for every second of his own time. That is, the received signal has been increased in frequency by the Doppler shift. These high frequency images are shown in the figures by blue light paths.
The asymmetry in the Doppler shifted images
The asymmetry between the earth and the space ship is manifested in this diagram by the factthat more blue-shifted (fast aging) images are received by the Ship. Put another way, the space ship sees the image change from a red-shift (slower aging of the image) to a blue-shift (faster aging of the image) at the mid-point of its trip (at the turnaround, 5 years after departure); the Earth sees the image of the ship change from red-shift to blue shift after 9 years (almost at the end of the period that the ship is absent). In the next section, one will see another asymmetry in the images: the Earth twin sees the ship twin age by the same amount in the red and blue shifted images; the ship twin sees the Earth twin age by different amounts in the red and blue shifted images.
Calculation of elapsed time from the Doppler diagram
The twin on the ship sees low frequency (red) images for 3 years. During that time, he would see the Earth twin in the image grow older by 3/3 = 1 years. He then sees high frequency (blue) images during the back trip of 3 years. During that time, he would see the Earth twin in the image grow older by 3 × 3 = 9 years. When the journey is finished, the image of the Earth twin has aged by 1 + 9 = 10 years.The Earth twin sees 9 years of slow (red) images of the ship twin, during which the ship twin ages (in the image) by 9/3 = 3 years. He then sees fast (blue) images for the remaining 1 year until the ship returns. In the fast images, the ship twin ages by 1 × 3 = 3 years. The total aging of the ship twin in the images received by Earth is 3 + 3 = 6 years, so the ship twin returns younger (6 years as opposed to 10 years on Earth).
The distinction between what they see and what they calculate
To avoid confusion, note the distinction between what each twin sees and what each would calculate. Each sees an image of his twin which he knows originated at a previous time and which he knows is Doppler shifted. He does not take the elapsed time in the image as the age of his twin now.- If he wants to calculate when his twin was the age shown in the image (i.e. how old he himself was then), he has to determine how far away his twin was when the signal was emitted—in other words, he has to consider simultaneity for a distant event.
- If he wants to calculate how fast his twin was aging when the image was transmitted, he adjusts for the Doppler shift. For example, when he receives high frequency images (showing his twin aging rapidly) with frequency
, he does not conclude that the twin was aging that rapidly when the image was generated, any more than he concludes that the siren of an ambulance is emitting the frequency he hears. He knows that the Doppler effectDoppler effectThe Doppler effect , named after Austrian physicist Christian Doppler who proposed it in 1842 in Prague, is the change in frequency of a wave for an observer moving relative to the source of the wave. It is commonly heard when a vehicle sounding a siren or horn approaches, passes, and recedes from...
has increased the image frequency by the factor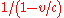
. Therefore he calculates that his twin was aging at the rate of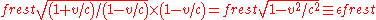
when the image was emitted. A similar calculation reveals that his twin was aging at the same reduced rate of
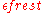
in all low frequency images.
Simultaneity in the Doppler shift calculation
It may be difficult to see where simultaneity came into the Doppler shift calculation, and indeed the calculation is often preferred because one does not have to worry about simultaneity. As seen above, the ship twin can convert his received Doppler-shifted rate to a slower rate of the clock of the distant clock for both red and blue images. If he ignores simultaneity, he might say his twin was aging at the reduced rate throughout the journey and therefore should be younger than he is. He is now back to square one, and has to take into account the change in his notion of simultaneity at the turnaround. The rate he can calculate for the image (corrected for Doppler effect) is the rate of the Earth twin's clock at the moment it was sent, not at the moment it was received. Since he receives an unequal number of red and blue shifted images, he should realize that the red and blue shifted emissions were not emitted over equal time periods for the Earth twin, and therefore he must account for simultaneity at a distance.Viewpoint of the traveling twin
During the turnaround, the traveling twin is in an accelerated reference frame. According to the equivalence principleEquivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
, the traveling twin may analyze the turnaround phase as if the stay-at-home twin were freely falling in a gravitational field and as if the traveling twin were stationary. A 1918 paper by Einstein presents a conceptual sketch of the idea.Einstein, A. (1918) "dialog about objections against the theory of relativity", Die Naturwissenschaften 48, pp. 697-702, 29 November 1918 From the viewpoint of the traveler, a calculation for each separate leg, ignoring the turnaround, leads to a result in which the Earth clocks age less than the traveler. For example, if the Earth clocks age 1 day less on each leg, the amount that the Earth clocks will lag behind amounts to 2 days. The physical description of what happens at turnaround has to produce a contrary effect of double that amount: 4 days' advancing of the Earth clocks. Then the traveler's clock will end up with a net 2-day delay on the Earth clocks, in agreement with calculations done in the frame of the stay-at-home twin.
The mechanism for the advancing of the stay-at-home twin's clock is gravitational time dilation
Gravitational time dilation
Gravitational time dilation is the effect of time passing at different rates in regions of different gravitational potential; the lower the gravitational potential, the more slowly time passes...
. When an observer finds that inertially moving objects are being accelerated with respect to themselves, those objects are in a gravitational field insofar as relativity is concerned. For the traveling twin at turnaround, this gravitational field fills the universe. In a weak field approximation, clocks tick at a rate of
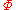where is the difference in gravitational potential. In this case, where g is the acceleration of the traveling observer during turnaround and h is the distance to the stay-at-home twin. The rocket is firing towards the stay-at-home twin, thereby placing that twin at a higher gravitational potential. Due to the large distance between the twins, the stay-at-home twin's clocks will appear to be sped up enough to account for the difference in proper times experienced by the twins. It is no accident that this speed-up is enough to account for the simultaneity shift described above. The general relativity solution for a static homogeneous gravitational field and the special relativity solution for finite acceleration produce identical results.Other calculations have been done for the traveling twin (or for any observer who sometimes accelerates), which do not involve the equivalence principle, and which do not involve any gravitational fields. Such calculations are based only on the special theory, not the general theory, of relativity. One
approach calculates surfaces of simultaneity by considering light pulses, in accordance with Hermann Bondi
Hermann Bondi
Sir Hermann Bondi, KCB, FRS was an Anglo-Austrian mathematician and cosmologist. He is best known for developing the steady-state theory of the universe with Fred Hoyle and Thomas Gold as an alternative to the Big Bang theory, but his most lasting legacy will probably be his important...
's idea of the k-calculus. A second approach calculates a straightforward but technically complicated integral to determine how the traveling twin measures the elapsed time on the stay-at-home clock. An outline of this second approach is given in a separate section below.
Difference in elapsed time as a result of differences in twins' spacetime paths
The following paragraph shows several things:- how to employ a precise mathematical approach in calculating the differences in the elapsed time
- how to prove exactly the dependency of the elapsed time on the different paths taken through spacetime by the two twins
- how to quantify the differences in elapsed time
- how to calculate proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
as a function (integral) of coordinate timeCoordinate timeIn the theory of relativity, it is convenient to express results in terms of a spacetime coordinate system relative to an implied observer. In many coordinate systems, an event is specified by one time coordinate and three spatial coordinates...
Let clock K be associated with the "stay at home twin".
Let clock K' be associated with the rocket that makes the trip.
At the departure event both clocks are set to 0.
- Phase 1: Rocket (with clock K') embarks with constant proper acceleration a during a time Ta as measured by clock K until it reaches some velocity V.
- Phase 2: Rocket keeps coasting at velocity V during some time Tc according to clock K.
- Phase 3: Rocket fires its engines in the opposite direction of K during a time Ta according to clock K until it is at rest with respect to clock K. The constant proper acceleration has the value -a, in other words the rocket is decelerating.
- Phase 4: Rocket keeps firing its engines in the opposite direction of K, during the same time Ta according to clock K, until K' regains the same speed V with respect to K, but now towards K (with velocity -V).
- Phase 5: Rocket keeps coasting towards K at speed V during the same time Tc according to clock K.
- Phase 6: Rocket again fires its engines in the direction of K, so it decelerates with a constant proper acceleration a during a time Ta, still according to clock K, until both clocks reunite.
Knowing that the clock K remains inertial (stationary), the total accumulated proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
of clock K' will be given by the integral function of coordinate timeCoordinate time
In the theory of relativity, it is convenient to express results in terms of a spacetime coordinate system relative to an implied observer. In many coordinate systems, an event is specified by one time coordinate and three spatial coordinates...
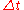
where v(t) is the coordinate velocity of clock K' as a function of t according to clock K, and, e.g. during phase 1, given by
This integral can be calculated for the 6 phases:
- Phase 1
- Phase 2
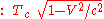
- Phase 3
- Phase 4
- Phase 5
- Phase 6
where a is the proper acceleration, felt by clock K' during the acceleration phase(s) and where the following relations hold between V, a and Ta:
So the traveling clock K' will show an elapsed time of
which can be expressed as
whereas the stationary clock K shows an elapsed time of
which is, for every possible value of a, Ta, Tc and V, larger than the reading of clock K':
Difference in elapsed times: how to calculate it from the ship
Note that the above formula
(here
is another customary notation for the time of the non-inertial observer ) gives us the dependence of the proper time on the time elapsed in the inertial frame , assumed the velocity 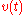is known. Actually, this equation answers the problem of the dependence between proper time and inertial time for the inertial observer at rest in but not for the moving observer. Indeed, the data 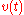is not always easily accessible from the ship. The observer in the non-inertial frame 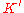may find it difficult to measure its velocity with respect to , not to mention that this velocity has to be parametrized with respect to the inertial time of , a step which needs the dependence between proper and inertial time to be known in advance. Can the non-inertial observer predict what will be the time elapsed for the twin which remained at home using only easily accessible data? The answer is affirmative and at least for a unidirectional motion has a simple answer given by-
where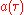
is the acceleration of the non-inertial observer as measured by himself (for instance with an accelerometer) in the whole round-trip and should not be confused with the non-relativistic acceleration
. It can also be shown that the inequality 
follows from the previous expression by using the Cauchy–Schwarz inequalityCauchy–Schwarz inequalityIn mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
:
-
A rotational version
Twins Bob and Alice inhabit a space station in circular orbit around a massive body in space. Bob departs the station and uses a rocket to hover in the fixed position where he left Alice, while she stays in the station. When the station completes an orbit and returns to Bob, he rejoins Alice. Alice is now younger than Bob. In addition to rotational acceleration, Bob must decelerate to become stationary and then accelerate again to match the orbital speed of the space station.
The time differential explanation in absolute terms
Special relativity can be formulated in absolute terms by assuming there is one frame whose measurements of length, time and simultaneity constitute the "true" values while observers moving relative to this frame are using rulers and clocks which are distorted according to the usual relativistic formulas. Specifically, in this context, the time differential of the twin paradox would be considered a consequence of "actual" clock slowing, with the clock changing frames being the clock which ticks the fewest times—the time registered on a clock being dependent on the combination of speed and distance covered in absolute terms. Often this notion is referred to as a type of Lorentz ether theoryLorentz ether theoryWhat is now often called Lorentz Ether theory has its roots in Hendrik Lorentz's "Theory of electrons", which was the final point in the development of the classical aether theories at the end of the 19th and at the beginning of the 20th century....
, which may be experimentally indistinguishable from the more common interpretation of relativity where no frame is preferred in any sense. A minority of physicists also favor some version of Mach's principleMach's principleIn theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
, which would imply that the difference between accelerated motion and inertial motion can only be defined relative to the rest of the matter in the universe, often referred to as motion relative to the "fixed stars". For example, A.P. French writes, regarding the twin paradox: "Note, though, that we are appealing to the reality of A's acceleration, and to the observability of the inertial forcesFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
associated with it. Would such effects as the twin paradox exist if the framework of fixed stars and distant galaxies were not there? Most physicists would say no. Our ultimate definition of an inertial frame may indeed be that it is a frame having zero acceleration with respect to the matter of the universe at large."
See also
- Herbert DingleHerbert DingleHerbert Dingle , an English physicist and natural philosopher, who served as president of the Royal Astronomical Society from 1951 to 1953, is best known for his opposition to Albert Einstein's special theory of relativity and the protracted controversy that this provoked.-Biography:Dingle was born...
- Bell's spaceship paradoxBell's spaceship paradoxBell's spaceship paradox is a thought experiment in special relativity involving accelerated spaceships and strings. The results of this thought experiment are for many people paradoxical. While J. S. Bell's 1976 version of the paradox is the most widely known, it was first designed by E. Dewan and M...
- Ehrenfest paradoxEhrenfest paradoxThe Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.In its original formulation as presented by Paul Ehrenfest 1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry...
- Ladder paradoxLadder paradoxThe ladder paradox is a thought experiment in special relativity. It involves a ladder travelling horizontally and undergoing a length contraction, the result of which being that it can fit into a much smaller garage...
- Supplee's paradoxSupplee's paradoxIn relativistic physics, Supplee's paradox arises when considering the buoyant force exerted on a relativistic bullet immersed in a fluid subject to an ambient gravitational field...
Further reading
The ideal clock
The ideal clock is a clock whose action depends only on its instantaneous velocity, and is independent of any acceleration of the clock.
Gravitational time dilation; time dilation in circular motion
External links
- Twin Paradox overview in the Usenet Physics FAQ
- The twin paradox: Is the symmetry of time dilation paradoxical? From Einsteinlight: Relativity in animations and film clips.
- FLASH Animations: from John de Pillis. (Scene 1): "View" from the Earth twin's point of view. (Scene 2): "View" from the traveling twin's point of view.
- Herbert Dingle
-