Galilean transformation
Encyclopedia
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation
point of view. The equations below, although apparently obvious, break down at speeds that approach the speed of light
due to physics described by relativity theory
.
Galileo
formulated these concepts in his description of uniform motion.
The topic was motivated by Galileo's description of the motion of a ball
rolling down a ramp
, by which he measured the numerical value for the acceleration
of gravity near the surface of the Earth
.
This assumption is abandoned in the Lorentz transformation
s. These relativistic
transformations are applicable to all velocities, whilst the Galilean transformation can be regarded as a low-velocity approximation to the Lorentz transformation.
The notation below describes the relationship under the Galilean transformation between the coordinates (x,y,z,t) and (x′,y′,z′,t′) of a single arbitrary event, as measured in two coordinate systems S and S', in uniform relative motion (velocity
v) in their common x and x’ directions, with their spatial origins coinciding at time t=t'=0:




Note that the last equation expresses the assumption of a universal time independent of the relative motion of different observers.
 Under the Erlangen program
Under the Erlangen program
, the space-time (no longer spacetime
) of nonrelativistic physics is described by the symmetry group
generated by Galilean transformations, spatial and time translations and rotations.
The Galilean symmetries (interpreted as active transformations):
Spatial translations: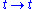
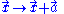
Time translations: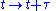

Shear mappings: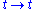
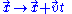
Rotations and Reflections: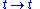
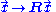
where R is an orthogonal matrix
.
: Here, we will only look at its Lie algebra
. It's easy to extend the results to the Lie group
. The Lie algebra of L is spanned
by H, Pi, Ci and Lij (antisymmetric tensor) subject to commutator
s, where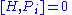

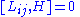
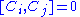

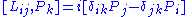
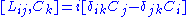
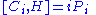
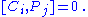
H is generator of time translations (Hamiltonian
), Pi is generator of translations (momentum operator
), Ci is generator of Galileian boosts and Lij stands for a generator of rotations (angular momentum operator
).
We can now give it a central extension into the Lie algebra spanned by H', P'i, C'i, L'ij (antisymmetric tensor
), M such that M commutes with everything (i.e. lies in the center
, that's why it's called a central extension) and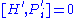


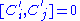
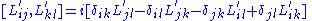
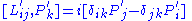
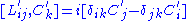
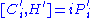
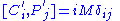
Active and passive transformation
In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
point of view. The equations below, although apparently obvious, break down at speeds that approach the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
due to physics described by relativity theory
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
Galileo
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
formulated these concepts in his description of uniform motion.
The topic was motivated by Galileo's description of the motion of a ball
Ball
A ball is a round, usually spherical but sometimes ovoid, object with various uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for simpler activities, such as catch, marbles and juggling...
rolling down a ramp
Inclined plane
The inclined plane is one of the original six simple machines; as the name suggests, it is a flat surface whose endpoints are at different heights. By moving an object up an inclined plane rather than completely vertical, the amount of force required is reduced, at the expense of increasing the...
, by which he measured the numerical value for the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of gravity near the surface of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
.
Translation
In essence, the Galilean transformations embody the intuitive notion of addition and subtraction of velocities. The assumption that time can be treated as absolute is at the heart of the Galilean transformations.This assumption is abandoned in the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s. These relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
transformations are applicable to all velocities, whilst the Galilean transformation can be regarded as a low-velocity approximation to the Lorentz transformation.
The notation below describes the relationship under the Galilean transformation between the coordinates (x,y,z,t) and (x′,y′,z′,t′) of a single arbitrary event, as measured in two coordinate systems S and S', in uniform relative motion (velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
v) in their common x and x’ directions, with their spatial origins coinciding at time t=t'=0:




Note that the last equation expresses the assumption of a universal time independent of the relative motion of different observers.
Galilean transformations

Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
, the space-time (no longer spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
) of nonrelativistic physics is described by the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
generated by Galilean transformations, spatial and time translations and rotations.
The Galilean symmetries (interpreted as active transformations):
Spatial translations:
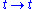
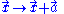
Time translations:
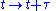

Shear mappings:
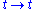
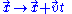
Rotations and Reflections:
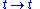
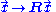
where R is an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
.
Central extension of the Galilean group
The Galilean groupRepresentation theory of the Galilean group
In nonrelativistic quantum mechanics, an account can be given of the existence of mass and spin as follows:The spacetime symmetry group of nonrelativistic quantum mechanics is the Galilean group...
: Here, we will only look at its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. It's easy to extend the results to the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. The Lie algebra of L is spanned
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by H, Pi, Ci and Lij (antisymmetric tensor) subject to commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s, where
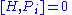

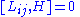
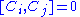

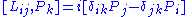
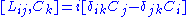
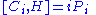
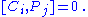
H is generator of time translations (Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
), Pi is generator of translations (momentum operator
Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
), Ci is generator of Galileian boosts and Lij stands for a generator of rotations (angular momentum operator
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
).
We can now give it a central extension into the Lie algebra spanned by H', P'i, C'i, L'ij (antisymmetric tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
), M such that M commutes with everything (i.e. lies in the center
Center (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
, that's why it's called a central extension) and
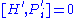


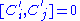
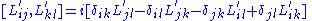
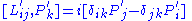
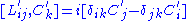
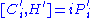
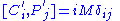
See also
- Representation theory of the Galilean groupRepresentation theory of the Galilean groupIn nonrelativistic quantum mechanics, an account can be given of the existence of mass and spin as follows:The spacetime symmetry group of nonrelativistic quantum mechanics is the Galilean group...
- Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
- Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
- Lagrangian and Eulerian coordinatesLagrangian and Eulerian coordinatesIn fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...

