
Mathematics and art
Encyclopedia
Mathematics and art have a long historical relationship. The ancient Egyptians
and ancient Greeks
knew about the golden ratio
, regarded as an aesthetically pleasing ratio, and incorporated it into the design of monuments including the Great Pyramid
, the Parthenon
, the Colosseum
. There are many examples of artists who have been inspired by mathematics
and studied mathematics as a means of complementing their works. The Greek sculptor Polykleitos
prescribed a series of mathematical proportions for carving the ideal male nude. Renaissance
painters turned to mathematics and many, including Piero della Francesca
, became accomplished mathematicians themselves.
in his Il Saggiatore wrote that “[The universe] is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures.” Artists who strive and seek to study nature must therefore first fully understand mathematics. On the other hand, mathematicians have sought to interpret and analyse art through the lens of geometry and rationality.
, roughly equal to 1.618, was first formally introduced in text by Greek mathematician Pythagoras
and later by Euclid
in the 5th century BC. In the fourth century BC, Aristotle
noted its aesthetic properties. Aside from interesting mathematical properties, geometric shapes derived from the golden ratio, such as the golden rectangle, the golden triangle, and Kepler’s triangle, were believed to be aesthetically pleasing. As such, many works of ancient art
exhibit and incorporate the golden ratio in their design. Various authors can discern the presence of the golden ratio in Egyptian, Summerian and Greek vases, Chinese pottery, Olmec sculptures, and Cretan and Mycenaean products from as early as the late Bronze Age. The prevalence of this special number in art and architecture even before its formal discovery by Pythagoras is perhaps evidence of an instinctive and primal human cognitive preference for the golden ratio.
 Evidence of mathematical influences in art is present in the Great Pyramids, built by Egyptian Pharaoh
Evidence of mathematical influences in art is present in the Great Pyramids, built by Egyptian Pharaoh
Khufu
and completed in 2560BC. Pyramidologists
since the nineteenth century have noted the presence of the golden ratio in the design of the ancient monuments. They note that the length of the base edges range from 755–756 feet while the height of the structure is 481.4 feet. Working out the math, the perpendicular bisector of the side of the pyramid comes out to 612 feet. If we divide the slant height of the pyramid by half its base length, we get a ratio of 1.619, less than 1% from the golden ratio. This would also indicate that half the cross-section of the Khufu’s pyramid is in fact a Kepler’s triangle. Debate has broken out between prominent pyramidologists
, including Temple Bell, Michael Rice, and John Taylor, over whether the presence of the golden ratio in the pyramids is due to design or chance. Of note, Rice contends that experts of Egyptian architecture have argued that ancient Egyptian architects have long known about the existence of the golden ratio. In addition, three other pyramidologists, Martin Gardner
, Herbert Turnbull, and David Burton contend that:
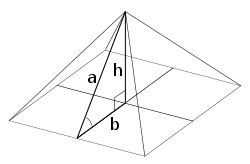
This passage, if true, would undeniably prove the intentional presence of the golden ratio in the pyramids. However, the validity of this assertion is found to be questionable.
Critics of this golden ratio theory note that it is far more likely that the original Egyptian architects modeled the pyramid after the 3-4-5 triangle
, rather than the Kepler’s triangle. According to the Rhind Mathematical Papyrus
, an ancient papyrus that is the best example of Egyptian
math dating back to the Second Intermediate Period of Egypt
, the Egyptians certainly knew about and used the 3-4-5 triangle extensively in mathematics and architecture. While Kepler’s triangle has a face angle of 51°49’, the 3-4-5 triangle has a face angle of 53°8’, very close to the Kepler’s triangle. Another triangle that is close is one whose perimeter is 2π the height such that the base to hypotenuse ratio is 1:4/π. With a face angle of 51°50’, it is also very similar to Kepler’s triangle. While the exact triangle the Egyptians chose to design their pyramids after remains unclear, the fact that the dimensions of pyramids correspond so strongly to a special right triangle suggest a strong mathematical influence in the last standing ancient wonder
.
is a temple
dedicated the Greek goddess Athena
, built in the 5th century BC on the Athenian Acropolis. It is contended that Phidias
, the main Greek sculptor in charge of decorating the Parthenon, also knew about the golden ratio and its aesthetic properties. In fact, the Greek symbol for the Golden Ratio is named Phi
(φ) because of Phidias
. The golden rectangle, a rectangle
whose length to width ratio is the golden ratio and considered the most pleasing to the eye, is almost omnipresent in the façade
and floor plans of the Parthenon
. The entire façade may be enclosed within a golden rectangle. The ratio of the length of a metope
and triglyph
to the height of the frieze
, as well as the height of the columns and stylobate
to the entire height of the temple is also the golden ratio. Phidias himself constructed many Parthenon statues that meticulously embody the golden ratio. Phidias is also notable for his contributions to the Athena Parthenos
and the Statue of Zeus. As with the Pyramids however, more recent historians challenge the purposeful inclusion of the golden ratio in Greek temples, such as the Parthenon, contending that earlier studies have purposefully fitted in measurements of the temple until it conformed to a golden rectangle.
in 670 A.D. in modern day Tunisia. Today, it exists as the first mosque
in North Africa, as well as the most famous one. Boussora and Mazouz’s study of the mosque dimensions reveal a very consistent application of the golden ratio in the mosque’s design. Boussora and Mazouz contend:
It should however be noted that the current floor plans of the mosque do not constitute a perfect rectangle, due to urban constraints. Even so, for example, the division of the court yard and prayer hall is almost a perfect golden ratio.
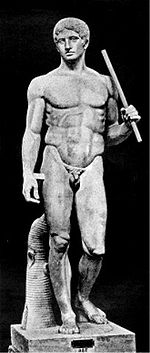 Polykleitos
Polykleitos
the Elder (c.450-420B.C.) was a Greek
sculptor from the school of Argos
who was also a contemporary of Phidias
. His works and statues consisted mainly of bronze and were of athletes. According to the mathematician Xenocrates
, Polykleitos is ranked as one of the most important sculptors of Classical antiquity
for his work on the Doryphorus and the statue of Hera
in the Heraion of Argos
. While his sculptures may not be as famous as those Phidias, he is better known for his approach towards sculpture. In the Canon of Polykleitos, a treatise he wrote designed to document the “perfect” anatomical
proportions of the male nude, Polykleitos gives us a mathematical approach towards sculpturing the human body. The influence of the Canon of Polykleitos is immense both in Classical Greek, Roman
, and Renaissance
sculpture, with many sculptors after him following Polykleitos’ prescription. While none of Polykleitos’ original works survive, Roman copies of his works demonstrate and embody his ideal of physical perfection and mathematical precision.
Some scholars contend the influence of the mathematician Pythagoras
on the Canon of Polykleitos. The Canon applies the basic mathematical concepts of Greek geometry, such as the ratio, proportion, and symmetria (Greek for “harmonious proportions”) and turns it into a system capable of describing the human form through a series of continuous geometric progressions. Polykleitos starts with a specific human body part, the distal phalanges
of the little finger
, or the tip of the little finger to the first joint, and establishes that as the basic module or unit for determining all the other proportions of the human body. From that, Polykleitos multiplies the length by radical 2 (1.14142) to get the distance of the second phalanges
and multiplies the length again by radical 2 to get the length of the third phalanges
. Next, he takes the finger
length and multiplies it again by radical 2 to get the length of the palm from the base of the finger to the ulna
. This geometric series of measurements progress until Polykleitos has formed the arm, chest, body, and so on. Other proportions are less set. For example, the ideal body should be 8 heads high and 2 heads wide. However, ordinary figures are 7½ heads tall while heroic figures are 8½ heads tall.
saw a rebirth of Classical Greek and Roman
culture and ideas, among them the study of mathematics as a relevant subject needed to understand nature
and the arts
. Two major reasons drove Renaissance artists towards the pursuit of mathematics. First, painters needed to figure out how to depict three-dimensional scenes on a two-dimensional canvas. Second, philosophers and artists alike were convinced that mathematics was the true essence of the physical world and that the entire universe, including the arts, could be explained in geometric terms. In light of these factors, Renaissance artists became some of the best applied mathematicians of their times.
(1397–1475) was fascinated by the study of perspective. A marble mosaic in the floor of the San Marco Basilica in Venice featuring the small stellated dodecahedron is attributed to Uccello.
 Piero della Francesca
Piero della Francesca
(c.1415-1492), an early Renaissance artist
from Italy
, exemplified this new shift in Renaissance thinking. Though chiefly appreciated for his art, he was an expert mathematician
and geometer and authored many books on solid geometry
and the emerging field of perspective
, including De Prospectiva Pingendi (On Perspective for Painting), Trattato d’Abaco (Abacus Treatise), and De corporibus regularibus (Regular Solids). Historian Vasari in the Lives of the Painters calls Piero the “greatest geometer of his time, or perhaps of any time.” He was deeply interested in the theoretical study of perspective and this was apparent in many of his paintings, including the S. Agostino altarpiece and The Flagellation of Christ. His work on geometry influenced later mathematicians and artists, including Luca Pacioli
in his De Divina Proportione and Leonardo da Vinci
.
Piero began his study of classical mathematics and the works of the Greek mathematician Archimedes
in the library at Urbino
. In addition to this classical training, Piero was taught commercial arithmetic in “abacus schools,” evidenced indirectly by his own writings which copies the format of abacus school textbooks. It is possible therefore that he was influenced by the works of Leonardo Pisano (Fibonacci
) from which those abacus textbooks were derived. Piero lived in the time when linear perspective was just being introduced in the artistic world. Leon Battista Alberti sums up the idea: “light rays travel in straight lines from points in the observed scene to the eye, forming a kind of pyramid
with the eye as vertex.” The painting therefore is a cross-sectional
plane of that pyramid. The study of perspective precedes Piero and the Renaissance however. Before perspective, artists typically sized objects and figures according to their thematic importance. Perspective was first observed in 5th century B.C. Greece
and Euclid’s
Optics
first introduced a mathematical theory of perspective. Muslim mathematician Alhazen extended the theory of optics in his Book of Optics
in 1021 A.D., although he never applied these principals to art. Perspective first exploded onto the Renaissance artistic scene with Giotto di Bondone
, who attempted to draw in perspective using an algebraic method to determine the placement of distant lines. In 1415, Italian architect
Filippo Brunelleschi
and his friend Leon Battista Alberti demonstrated the geometrical method of applying perspective in Florence, centered around the usage of similar triangles, a mathematical concept formulated long ago by Euclid, in determining the apparent height of distant objects. However, Piero is the first painter to write a practical treatise for the application of this idea in art in his De Prospectiva Pingendi.
 In De Prospectiva Pingendi, Peiro painstakingly transforms art and his empirical observations into “vera scientia” (true science), i.e. into mathematical proofs. His treatise starts like any mathematics book in the vein of Euclid: he defines the point as “essere una costa tanto picholina quanto e possible ad ochio comprendere” (being the tiniest thing that is possible for the eye to comprehend). From there, Piero uses a series of deductive logic to lead us, theorem by theorem, to the perspective representation of a three-dimensional body. Piero realized that the way aspects of a figure changed with the point of view obeyed precise and determinable mathematical laws. Piero methodically presented a series of perspective problems to gradually ease his reader from easy to increasingly complex problems. Mark Peterson explains:
In De Prospectiva Pingendi, Peiro painstakingly transforms art and his empirical observations into “vera scientia” (true science), i.e. into mathematical proofs. His treatise starts like any mathematics book in the vein of Euclid: he defines the point as “essere una costa tanto picholina quanto e possible ad ochio comprendere” (being the tiniest thing that is possible for the eye to comprehend). From there, Piero uses a series of deductive logic to lead us, theorem by theorem, to the perspective representation of a three-dimensional body. Piero realized that the way aspects of a figure changed with the point of view obeyed precise and determinable mathematical laws. Piero methodically presented a series of perspective problems to gradually ease his reader from easy to increasingly complex problems. Mark Peterson explains:

In his 1919 book Ad Quadratum, Frederik Macody Lund
, a historian who studied the geometry of several gothic structures, claims that the Cathedral of Chartres
(begun in the 12th century), the Notre-Dame of Laon
(1157–1205), and the Notre Dame de Paris
(1160) are designed according to the golden ratio
. According to Macody Lund, the superimposed regulator lines show that the cathedral has golden proportions. Other scholars argue that until Pacioli's 1509 publication, the golden ratio was unknown to artists and architects.
 Albrecht Dürer
Albrecht Dürer
(1471–1528) was a German Renaissance
printmaker who made important contributions to polyhedral literature in his book, Underweysung der Messung (Four Books on Measurement) (1525), meant to teach the subjects of linear perspective, geometry
in architecture
, Platonic solids, and regular polygons. Dürer was likely influenced by the works of Luca Pacioli
and Piero della Francesca
during his trips to Italy
. While the examples of perspective in Underweysung der Messung are underdeveloped and contain a number of inaccuracies, the manual does contain a very interesting discussion of polyhedra. Dürer is also the first to introduce in text the idea of polyhedral nets
, polyhedra unfolded to lie flat for printing. Dürer published another influential book on human proportions called Vier Bücher von Menschlicher Proportion (Four Books on Human Proportion) in 1528.
Dürer's well-known engraving Melancholia I depicts a frustrated thinker sitting by what is best interpreted as a “truncated rhomboid” or a “rhombohedron with 72-degree face angles, which has been truncated so it can be inscribed in a sphere”. It has been the subject of more modern interpretation than almost any other print, including a two-volume book by Peter-Klaus Schuster, and a very influential discussion in Erwin Panofsky
's monograph of Dürer.
One might speculate that the cube represents masculinity and truncating one in an upright position may have some Freudian symbolism.
 Written by Luca Pacioli
Written by Luca Pacioli
in Milan
from 1496–98, published in Venice
in 1509, De Divina Proportione
was about mathematical and artistic proportion. Leonardo da Vinci
drew illustrations of regular solids in De divina proportione while he lived with and took mathematics lessons from Pacioli. Leonardo's drawings are probably the first illustrations of skeletonic solids, which allowed an easy distinction between front and back. Skeletonic solids, such as the rhombicuboctahedron
, were one of the first solids drawn to demonstrate perspective by being overlaid on top of each other. Additionally, the work also discusses the use of perspective by painters such as Piero della Francesca
, Melozzo da Forlì
, and Marco Palmezzano
.
It is in De Divina Proportione that the golden ratio is defined as the divine proportion. Pacioli also details the use of the golden ratio as the mathematical definition of beauty when applied to the human face.
 Leonardo da Vinci
Leonardo da Vinci
(1452–1519) was an Italian scientist
, mathematician
, engineer
, inventor, anatomist, painter
, sculptor, and architect
. Leonardo has often been described as the archetype of the Renaissance man.
Renowned primarily as a painter, Leonardo incorporated many mathematical concepts into his artwork despite never having received any formal mathematical training. It was not until the 1490s that he trained under Luca Pacioli
and prepared a series of drawings for De Divina Proportione. Leonardo studied Pacioli's Summa, from which he copied tables of proportions and multiplication tables.
Notably in Mona Lisa and The Last Supper, Leonardo’s work incorporated the concept of linear perspective. By making all of the lines in the painting converge on a single, invisible point on the horizon, a flat painting can appear to have depth. In creating the vanishing point
, Leonardo creates the illusion that the painting is an extension of the room itself.
 In Mona Lisa
In Mona Lisa
, one can observe the mismatch between the left and right backgrounds which creates the illusion of perspective and depth. It is believed that Leonardo, as a mathematician, purposefully made this painting line up with Golden Rectangles in this fashion in order to further the incorporation of mathematics into art. A Golden Rectangle whose base extends from her right wrist to her left elbow and reaches the top of her very head can be constructed. This Golden Rectangle can be then further subdivided into smaller Golden Rectangles and can be drawn to produce the Golden Spiral. Also a viewer can note that all these edges of the new rectangles come to intersect the focal points of Mona Lisa: chin, eye, nose, and upturned corner of her mouth. It is also worth mentioning that the overall shape of the woman is a triangle with her arms as the base and her head as the tip. This is meant to draw attention to the face of the woman in the portrait.
 In The Last Supper, Leonardo sought to create a perfect harmonic balance between the placement of the characters and the background. He did intensive studies on how the characters should be arranged at the table. The entire painting was constructed in a tight ratio of 12:6:4:3. The entire piece measures 6 by 12 units. The wall in the back is equal to 4 units. The windows are 3 units and the recession of the tapestries on the side walls is 12:6:4:3.
In The Last Supper, Leonardo sought to create a perfect harmonic balance between the placement of the characters and the background. He did intensive studies on how the characters should be arranged at the table. The entire painting was constructed in a tight ratio of 12:6:4:3. The entire piece measures 6 by 12 units. The wall in the back is equal to 4 units. The windows are 3 units and the recession of the tapestries on the side walls is 12:6:4:3.
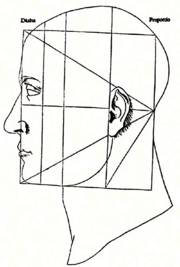
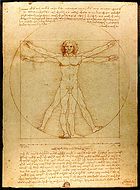
In Vitruvian Man
, Leonardo used both image and text to express the ideas and theories of Vitruvius
, a first century Roman architect and author of De Architectura libri X. The Vitruvian ideas formed the basis of Renaissance proportion theories in art and architecture. Various artists and architects had illustrated Vitruvius' theory prior to Leonardo, but Leonardo's drawing differs from the previous works in that the male figure adopts two different positions within the same image. He is simultaneously within the circle and the square; movement and liveliness are suggested by the figure's active arms and legs.
The thin lines on his form show the significant points of the proportion scheme. These lines indicate Leonardo’s concern with the architectural meaning of the work. Leonardo is representing the body as a building and illustrating Renaissance theory which linked the proportions of the human body with architectural planning.
.svg.png) Named after Roger Penrose, Penrose tiles are nonperiodic tiles generated from a simple base tile. In its simplest form, it consists of 36- and 72-degree rhombuses, with "matching rules" forcing the rhombuses to line up against each other only in certain patterns. Penrose tiles lack translational symmetry
Named after Roger Penrose, Penrose tiles are nonperiodic tiles generated from a simple base tile. In its simplest form, it consists of 36- and 72-degree rhombuses, with "matching rules" forcing the rhombuses to line up against each other only in certain patterns. Penrose tiles lack translational symmetry
due to its nonperiodicity, and any finite region in a tiling appears infinitely many times in the tiling.
Both visually complex and simple at the same time, Penrose tiles arise from basic mathematical principles and can be viewed as intricately related to the golden ratio. Two notable relationships between Penrose tiles and the Golden ratio are:
The Core, a new education building, was constructed with the inspiration of the Fibonacci Numbers and plant spirals. From a top down view, one can see the building’s windows aligned in a spiral similar to the golden spiral
and plant spirals.
. Campus buildings were designed around the concept of the golden spiral which is defined at the very center by the three core buildings. The outward spiraling arc can be seen below and extends throughout the campus.
 A renowned artist born in 1898 and died in 1972, M.C. Escher was known for his mathematically inspired work. Escher’s interest in tessellations, polyhedrons, shaping of space, and self-reference manifested itself in his work throughout his career. In the Alhambra Sketch, Escher showed that art can be created with polygons or regular shapes such as triangles, squares, and hexagons. Escher used irregular polygons when tiling the plane and often used reflections, glide reflection
A renowned artist born in 1898 and died in 1972, M.C. Escher was known for his mathematically inspired work. Escher’s interest in tessellations, polyhedrons, shaping of space, and self-reference manifested itself in his work throughout his career. In the Alhambra Sketch, Escher showed that art can be created with polygons or regular shapes such as triangles, squares, and hexagons. Escher used irregular polygons when tiling the plane and often used reflections, glide reflection
s, and translations
to obtain many more patterns. Additionally, Escher arranged the shapes to simulate images of animals and other figures.
His work can be noted in Development 1 and Cycles.
Escher’s was also interested in a specific type of polyhedron that appears many times in his work. These polyhedrons are defined as solids that have exactly similar polygonal faces, also known as Platonic solids. These Platonic solids, tetrahedrons, cubes, octahedrons, dodecahedrons, and icosahedrons stellations are especially prominent in Order and Chaos and Four Regular Solids. Here these stellated figures often reside within another figure which further distorts the viewing angle and conformation of the polyhedrons and providing a multifaceted perspective artwork.
Additionally, Escher worked with the shape and logic of space in Three Intersecting Planes, Snakes
, High and Low, and Waterfall
.
Many of Escher's works contain impossible constructions, made using geometrical objects that cannot exist but are pleasant to the human sight. Some of Escher's tessellation
drawings were inspired by conversations with the mathematician H. S. M. Coxeter concerning hyperbolic geometry
. Relationships between the works of mathematician Kurt Gödel
, artist M. C. Escher
and composer Johann Sebastian Bach
are explored in Gödel, Escher, Bach
, a Pulitzer Prize
-winning book.
 Salvador Dalí (1904–1989) incorporated mathematical themes in several of his later works. His 1954 painting Crucifixion (Corpus Hypercubus)
Salvador Dalí (1904–1989) incorporated mathematical themes in several of his later works. His 1954 painting Crucifixion (Corpus Hypercubus)
depicts a crucified figure upon the net of a hypercube
. In The Sacrament of the Last Supper
(1955) Christ and his disciples are pictured inside a giant dodecahedron. Dali's last painting, The Swallow's Tail
(1983), was part of a series inspired by René Thom
's catastrophe theory
.
(1969–2007) was a contemporary Spanish painter and sculptor focused on the investigation of form. Heavily influenced by cubism and Paul Klee, Palazuelo developed a unique style that he described as the geometry of life and the geometry of all nature. Consisting of simple geometric shapes with detailed patterning and coloring, Palazuelo’s work was noted as powerful, attractive, unhesitant, enigmatic, and always new. From works such as Angular I to Automnes, Palazuelo expressed himself in geometric transformations and translations. Over time as Carmen Bonell notes, Palazuelo’s work evolved very rapidly toward an abstract-geometric language of increasing purity.
(1935–2007) was originally a sheep farmer who turned to sculpting. He began a serious sculpting career at the age of 35. Robinson was deeply interested in astronomy
and mathematical relationships. According to Ronald Brown, Robinson’s work was extraordinary because of its proportion, line, rhythm, finish, the resonance of the titles and the forms, and because some of the complex forms, such as Rhythm of Life, had hardly been visualized in such an exact way. Robinson’s work from Gordian Knot to Bands of Friendship displayed highly complex mathematical knot theory in polished bronze for the public to see.
Many mathematicians working in the field of topology
and specifically with torus
es see mathematical relationships in Robinson’s sculptures.
Rhythm of Life arose from experiments with wrapping a ribbon around an inner tube and finding it returned to itself.
Genesis evolved from an attempt at making Borromean rings-a set of three circles, no two of which link but in which the whole structure cannot be taken apart without breaking.
Many of Robinson’s works express the theme of common humanity. In Dependent Beings, the sculpture comprises a square that twists as it travels around the circle, giving it a boundary of two strips in contrasting textures.
has made sculptures in various materials of a wide range of complex surface
s and other topological objects
. His work is motivated specifically by the desire to create visual representations of mathematical objects.
Ferguson has created a sculpture called The Eightfold Way at the Berkeley, California, Mathematical Sciences Research Institute based on the projective special linear group PSL(2,7)
, a finite group of 168 elements.

The processing power of modern computers allows mathematicians and non-mathematicians to visualise complex mathematical objects such as the Mandelbrot set
. In the modern industry of computer animation
, fractal
s play a key role in modelling mountains, fire, trees and other natural objects.
s and other polyhedra
are a recurring theme in Western art. Examples include:
History of Egypt
Egyptian history can be roughly divided into the following periods:*Prehistoric Egypt*Ancient Egypt**Early Dynastic Period of Egypt: 31st to 27th centuries BC**Old Kingdom of Egypt: 27th to 22nd centuries BC...
and ancient Greeks
History of Greece
The history of Greece encompasses the history of the territory of the modern state of Greece, as well as that of the Greek people and the areas they ruled historically. The scope of Greek habitation and rule has varied much through the ages, and, as a result, the history of Greece is similarly...
knew about the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, regarded as an aesthetically pleasing ratio, and incorporated it into the design of monuments including the Great Pyramid
Great Pyramid of Giza
The Great Pyramid of Giza is the oldest and largest of the three pyramids in the Giza Necropolis bordering what is now El Giza, Egypt. It is the oldest of the Seven Wonders of the Ancient World, and the only one to remain largely intact...
, the Parthenon
Parthenon
The Parthenon is a temple on the Athenian Acropolis, Greece, dedicated to the Greek goddess Athena, whom the people of Athens considered their virgin patron. Its construction began in 447 BC when the Athenian Empire was at the height of its power. It was completed in 438 BC, although...
, the Colosseum
Colosseum
The Colosseum, or the Coliseum, originally the Flavian Amphitheatre , is an elliptical amphitheatre in the centre of the city of Rome, Italy, the largest ever built in the Roman Empire...
. There are many examples of artists who have been inspired by mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and studied mathematics as a means of complementing their works. The Greek sculptor Polykleitos
Polykleitos
Polykleitos ; called the Elder, was a Greek sculptor in bronze of the fifth and the early 4th century BCE...
prescribed a series of mathematical proportions for carving the ideal male nude. Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
painters turned to mathematics and many, including Piero della Francesca
Piero della Francesca
Piero della Francesca was a painter of the Early Renaissance. As testified by Giorgio Vasari in his Lives of the Artists, to contemporaries he was also known as a mathematician and geometer. Nowadays Piero della Francesca is chiefly appreciated for his art. His painting was characterized by its...
, became accomplished mathematicians themselves.
Overview
Galileo GalileiGalileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
in his Il Saggiatore wrote that “[The universe] is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures.” Artists who strive and seek to study nature must therefore first fully understand mathematics. On the other hand, mathematicians have sought to interpret and analyse art through the lens of geometry and rationality.
The Golden Ratio
The Golden RatioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, roughly equal to 1.618, was first formally introduced in text by Greek mathematician Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
and later by Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
in the 5th century BC. In the fourth century BC, Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
noted its aesthetic properties. Aside from interesting mathematical properties, geometric shapes derived from the golden ratio, such as the golden rectangle, the golden triangle, and Kepler’s triangle, were believed to be aesthetically pleasing. As such, many works of ancient art
Ancient art
Arts of the ancient world refer to the many types of art that were in the cultures of ancient societies, such as those of ancient China, India, Mesopotamia, Persia, Egypt, Greece and Rome.-Egypt:...
exhibit and incorporate the golden ratio in their design. Various authors can discern the presence of the golden ratio in Egyptian, Summerian and Greek vases, Chinese pottery, Olmec sculptures, and Cretan and Mycenaean products from as early as the late Bronze Age. The prevalence of this special number in art and architecture even before its formal discovery by Pythagoras is perhaps evidence of an instinctive and primal human cognitive preference for the golden ratio.
Pyramids

Pharaoh
Pharaoh is a title used in many modern discussions of the ancient Egyptian rulers of all periods. The title originates in the term "pr-aa" which means "great house" and describes the royal palace...
Khufu
Khufu
Khufu , also known as Cheops or, in Manetho, Suphis , was a Pharaoh of Ancient Egypt's Old Kingdom. He reigned from around 2589 to 2566 BC. Khufu was the second pharaoh of the Fourth Dynasty. He is generally accepted as being the builder of the Great Pyramid of Giza, one of the Seven Wonders of...
and completed in 2560BC. Pyramidologists
Pyramidology
Pyramidology is a term used, sometimes disparagingly, to refer to various pseudoscientific speculations regarding pyramids, most often the Giza Necropolis and the Great Pyramid of Giza in Egypt...
since the nineteenth century have noted the presence of the golden ratio in the design of the ancient monuments. They note that the length of the base edges range from 755–756 feet while the height of the structure is 481.4 feet. Working out the math, the perpendicular bisector of the side of the pyramid comes out to 612 feet. If we divide the slant height of the pyramid by half its base length, we get a ratio of 1.619, less than 1% from the golden ratio. This would also indicate that half the cross-section of the Khufu’s pyramid is in fact a Kepler’s triangle. Debate has broken out between prominent pyramidologists
Pyramidology
Pyramidology is a term used, sometimes disparagingly, to refer to various pseudoscientific speculations regarding pyramids, most often the Giza Necropolis and the Great Pyramid of Giza in Egypt...
, including Temple Bell, Michael Rice, and John Taylor, over whether the presence of the golden ratio in the pyramids is due to design or chance. Of note, Rice contends that experts of Egyptian architecture have argued that ancient Egyptian architects have long known about the existence of the golden ratio. In addition, three other pyramidologists, Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
, Herbert Turnbull, and David Burton contend that:

HerodotusHerodotusHerodotus was an ancient Greek historian who was born in Halicarnassus, Caria and lived in the 5th century BC . He has been called the "Father of History", and was the first historian known to collect his materials systematically, test their accuracy to a certain extent and arrange them in a...
related in one passage that the Egyptian priests told him that the dimensions of the Great Pyramid were so chosen that the area of a square whose side was the height of the great pyramid equaled the area of the triangle.
This passage, if true, would undeniably prove the intentional presence of the golden ratio in the pyramids. However, the validity of this assertion is found to be questionable.
Critics of this golden ratio theory note that it is far more likely that the original Egyptian architects modeled the pyramid after the 3-4-5 triangle
Special right triangles
A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45-45-90. This is called an "angle-based" right triangle...
, rather than the Kepler’s triangle. According to the Rhind Mathematical Papyrus
Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
, an ancient papyrus that is the best example of Egyptian
Ancient Egypt
Ancient Egypt was an ancient civilization of Northeastern Africa, concentrated along the lower reaches of the Nile River in what is now the modern country of Egypt. Egyptian civilization coalesced around 3150 BC with the political unification of Upper and Lower Egypt under the first pharaoh...
math dating back to the Second Intermediate Period of Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
, the Egyptians certainly knew about and used the 3-4-5 triangle extensively in mathematics and architecture. While Kepler’s triangle has a face angle of 51°49’, the 3-4-5 triangle has a face angle of 53°8’, very close to the Kepler’s triangle. Another triangle that is close is one whose perimeter is 2π the height such that the base to hypotenuse ratio is 1:4/π. With a face angle of 51°50’, it is also very similar to Kepler’s triangle. While the exact triangle the Egyptians chose to design their pyramids after remains unclear, the fact that the dimensions of pyramids correspond so strongly to a special right triangle suggest a strong mathematical influence in the last standing ancient wonder
Seven Wonders of the Ancient World
The Seven Wonders of the World refers to remarkable constructions of classical antiquity listed by various authors in guidebooks popular among the ancient Hellenic tourists, particularly in the 1st and 2nd centuries BC...
.
Parthenon
The ParthenonParthenon
The Parthenon is a temple on the Athenian Acropolis, Greece, dedicated to the Greek goddess Athena, whom the people of Athens considered their virgin patron. Its construction began in 447 BC when the Athenian Empire was at the height of its power. It was completed in 438 BC, although...
is a temple
Temple
A temple is a structure reserved for religious or spiritual activities, such as prayer and sacrifice, or analogous rites. A templum constituted a sacred precinct as defined by a priest, or augur. It has the same root as the word "template," a plan in preparation of the building that was marked out...
dedicated the Greek goddess Athena
Athena
In Greek mythology, Athena, Athenê, or Athene , also referred to as Pallas Athena/Athene , is the goddess of wisdom, courage, inspiration, civilization, warfare, strength, strategy, the arts, crafts, justice, and skill. Minerva, Athena's Roman incarnation, embodies similar attributes. Athena is...
, built in the 5th century BC on the Athenian Acropolis. It is contended that Phidias
Phidias
Phidias or the great Pheidias , was a Greek sculptor, painter and architect, who lived in the 5th century BC, and is commonly regarded as one of the greatest of all sculptors of Classical Greece: Phidias' Statue of Zeus at Olympia was one of the Seven Wonders of the Ancient World...
, the main Greek sculptor in charge of decorating the Parthenon, also knew about the golden ratio and its aesthetic properties. In fact, the Greek symbol for the Golden Ratio is named Phi
Phi
Phi may refer to:In language:*Phi, the Greek letter Φ,φ, the symbol for voiceless bilabial fricativeIn mathematics:*The Golden ratio*Euler's totient function*A statistical measure of association reported with the chi-squared test...
(φ) because of Phidias
Phidias
Phidias or the great Pheidias , was a Greek sculptor, painter and architect, who lived in the 5th century BC, and is commonly regarded as one of the greatest of all sculptors of Classical Greece: Phidias' Statue of Zeus at Olympia was one of the Seven Wonders of the Ancient World...
. The golden rectangle, a rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
whose length to width ratio is the golden ratio and considered the most pleasing to the eye, is almost omnipresent in the façade
Facade
A facade or façade is generally one exterior side of a building, usually, but not always, the front. The word comes from the French language, literally meaning "frontage" or "face"....
and floor plans of the Parthenon
Parthenon
The Parthenon is a temple on the Athenian Acropolis, Greece, dedicated to the Greek goddess Athena, whom the people of Athens considered their virgin patron. Its construction began in 447 BC when the Athenian Empire was at the height of its power. It was completed in 438 BC, although...
. The entire façade may be enclosed within a golden rectangle. The ratio of the length of a metope
Metope (architecture)
In classical architecture, a metope is a rectangular architectural element that fills the space between two triglyphs in a Doric frieze, which is a decorative band of alternating triglyphs and metopes above the architrave of a building of the Doric order...
and triglyph
Triglyph
Triglyph is an architectural term for the vertically channeled tablets of the Doric frieze, so called because of the angular channels in them, two perfect and one divided, the two chamfered angles or hemiglyphs being reckoned as one. The square recessed spaces between the triglyphs on a Doric...
to the height of the frieze
Frieze
thumb|267px|Frieze of the [[Tower of the Winds]], AthensIn architecture the frieze is the wide central section part of an entablature and may be plain in the Ionic or Doric order, or decorated with bas-reliefs. Even when neither columns nor pilasters are expressed, on an astylar wall it lies upon...
, as well as the height of the columns and stylobate
Stylobate
In classical Greek architecture, a stylobate is the top step of the crepidoma, the stepped platform on which colonnades of temple columns are placed...
to the entire height of the temple is also the golden ratio. Phidias himself constructed many Parthenon statues that meticulously embody the golden ratio. Phidias is also notable for his contributions to the Athena Parthenos
Athena Parthenos
Athena Parthenos was the title of a massive chryselephantine sculpture of the Greek goddess Athena made by Phidias and housed in the Parthenon in Athens. Its epithet was an essential character of the goddess herself...
and the Statue of Zeus. As with the Pyramids however, more recent historians challenge the purposeful inclusion of the golden ratio in Greek temples, such as the Parthenon, contending that earlier studies have purposefully fitted in measurements of the temple until it conformed to a golden rectangle.
Great Mosque of Kairouan
The Great Mosque of Kairouan was built by Uqba ibn NafiUqba ibn Nafi
Uqba ibn Nafi was an Arab hero and general who was serving the Umayyad dynasty, in Amir Muavia and Yazid periods, who began the Islamic conquest of the Maghreb, including present-day Algeria, Tunisia, Libya and Morocco in North Africa. He was the nephew of 'Amr ibn al-'As. Uqba is often surnamed...
in 670 A.D. in modern day Tunisia. Today, it exists as the first mosque
Mosque
A mosque is a place of worship for followers of Islam. The word is likely to have entered the English language through French , from Portuguese , from Spanish , and from Berber , ultimately originating in — . The Arabic word masjid literally means a place of prostration...
in North Africa, as well as the most famous one. Boussora and Mazouz’s study of the mosque dimensions reveal a very consistent application of the golden ratio in the mosque’s design. Boussora and Mazouz contend:
The geometric technique of construction of the golden section seems to have determined the major decisions of the spatial organisation. The golden section appears repeatedly in some part of the building measurements. It is found in the overall proportion of the plan and in the dimensioning of the prayer space, the court and the minaret. The existence of the golden section in some parts of Kairouan mosque indicates that the elements designed and generated with this principle may have been realised at the same period.
It should however be noted that the current floor plans of the mosque do not constitute a perfect rectangle, due to urban constraints. Even so, for example, the division of the court yard and prayer hall is almost a perfect golden ratio.
Polykleitos

Polykleitos
Polykleitos ; called the Elder, was a Greek sculptor in bronze of the fifth and the early 4th century BCE...
the Elder (c.450-420B.C.) was a Greek
Greeks
The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....
sculptor from the school of Argos
Argos
Argos is a city and a former municipality in Argolis, Peloponnese, Greece. Since the 2011 local government reform it is part of the municipality Argos-Mykines, of which it is a municipal unit. It is 11 kilometres from Nafplion, which was its historic harbour...
who was also a contemporary of Phidias
Phidias
Phidias or the great Pheidias , was a Greek sculptor, painter and architect, who lived in the 5th century BC, and is commonly regarded as one of the greatest of all sculptors of Classical Greece: Phidias' Statue of Zeus at Olympia was one of the Seven Wonders of the Ancient World...
. His works and statues consisted mainly of bronze and were of athletes. According to the mathematician Xenocrates
Xenocrates
Xenocrates of Chalcedon was a Greek philosopher, mathematician, and leader of the Platonic Academy from 339/8 to 314/3 BC. His teachings followed those of Plato, which he attempted to define more closely, often with mathematical elements...
, Polykleitos is ranked as one of the most important sculptors of Classical antiquity
Classical antiquity
Classical antiquity is a broad term for a long period of cultural history centered on the Mediterranean Sea, comprising the interlocking civilizations of ancient Greece and ancient Rome, collectively known as the Greco-Roman world...
for his work on the Doryphorus and the statue of Hera
Hera
Hera was the wife and one of three sisters of Zeus in the Olympian pantheon of Greek mythology and religion. Her chief function was as the goddess of women and marriage. Her counterpart in the religion of ancient Rome was Juno. The cow and the peacock were sacred to her...
in the Heraion of Argos
Heraion of Argos
The Heraion of Argos was the temple in the greatest sanctuary in the Argolid, dedicated to Hera, whose epithet "Argive Hera" , is familiar to readers of Homer. Hera herself claims to be the protector of Argos in Iliad IV, 50–52): "The three towns I love best are Argos, Sparta and Mycenae of...
. While his sculptures may not be as famous as those Phidias, he is better known for his approach towards sculpture. In the Canon of Polykleitos, a treatise he wrote designed to document the “perfect” anatomical
Anatomy
Anatomy is a branch of biology and medicine that is the consideration of the structure of living things. It is a general term that includes human anatomy, animal anatomy , and plant anatomy...
proportions of the male nude, Polykleitos gives us a mathematical approach towards sculpturing the human body. The influence of the Canon of Polykleitos is immense both in Classical Greek, Roman
Ancient Rome
Ancient Rome was a thriving civilization that grew on the Italian Peninsula as early as the 8th century BC. Located along the Mediterranean Sea and centered on the city of Rome, it expanded to one of the largest empires in the ancient world....
, and Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
sculpture, with many sculptors after him following Polykleitos’ prescription. While none of Polykleitos’ original works survive, Roman copies of his works demonstrate and embody his ideal of physical perfection and mathematical precision.
Some scholars contend the influence of the mathematician Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
on the Canon of Polykleitos. The Canon applies the basic mathematical concepts of Greek geometry, such as the ratio, proportion, and symmetria (Greek for “harmonious proportions”) and turns it into a system capable of describing the human form through a series of continuous geometric progressions. Polykleitos starts with a specific human body part, the distal phalanges
Distal phalanges
The distal or terminal phalanges are the terminal limb bones located at the tip of the digits...
of the little finger
Little finger
The little finger, often called the pinky in American English, pinkie in Scottish English , or small finger in medicine, is the most ulnar and usually smallest finger of the human hand, opposite the thumb, next to the ring finger.-Muscles:There are four muscles that...
, or the tip of the little finger to the first joint, and establishes that as the basic module or unit for determining all the other proportions of the human body. From that, Polykleitos multiplies the length by radical 2 (1.14142) to get the distance of the second phalanges
Intermediate phalanges
Intermediate phalanges are bones found in the limbs of most vertebrates. In humans, they are the bones of the finger and toe which lie in the middle, between the two wrinkly joints. The thumb and big toe do not have intermediate phalanges...
and multiplies the length again by radical 2 to get the length of the third phalanges
Proximal phalanges
Proximal phalanges are bones found in the limbs of most vertebrates. In humans, they are the bones at the base of a toe or finger, the prominent, knobby ends of which are often called the knuckles....
. Next, he takes the finger
Finger
A finger is a limb of the human body and a type of digit, an organ of manipulation and sensation found in the hands of humans and other primates....
length and multiplies it again by radical 2 to get the length of the palm from the base of the finger to the ulna
Ulna
The ulna is one of the two long bones in the forearm, the other being the radius. It is prismatic in form and runs parallel to the radius, which is shorter and smaller. In anatomical position The ulna is one of the two long bones in the forearm, the other being the radius. It is prismatic in form...
. This geometric series of measurements progress until Polykleitos has formed the arm, chest, body, and so on. Other proportions are less set. For example, the ideal body should be 8 heads high and 2 heads wide. However, ordinary figures are 7½ heads tall while heroic figures are 8½ heads tall.
Renaissance
The RenaissanceRenaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
saw a rebirth of Classical Greek and Roman
Ancient Rome
Ancient Rome was a thriving civilization that grew on the Italian Peninsula as early as the 8th century BC. Located along the Mediterranean Sea and centered on the city of Rome, it expanded to one of the largest empires in the ancient world....
culture and ideas, among them the study of mathematics as a relevant subject needed to understand nature
Nature
Nature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
and the arts
ARts
aRts, which stands for analog Real time synthesizer, is an audio framework that is no longer under development. It is best known for previously being used in KDE to simulate an analog synthesizer....
. Two major reasons drove Renaissance artists towards the pursuit of mathematics. First, painters needed to figure out how to depict three-dimensional scenes on a two-dimensional canvas. Second, philosophers and artists alike were convinced that mathematics was the true essence of the physical world and that the entire universe, including the arts, could be explained in geometric terms. In light of these factors, Renaissance artists became some of the best applied mathematicians of their times.
Paolo Uccello
Italian painter Paolo UccelloPaolo Uccello
Paolo Uccello , born Paolo di Dono, was an Italian painter and a mathematician who was notable for his pioneering work on visual perspective in art. Giorgio Vasari in his book Lives of the Artists wrote that Uccello was obsessed by his interest in perspective and would stay up all night in his...
(1397–1475) was fascinated by the study of perspective. A marble mosaic in the floor of the San Marco Basilica in Venice featuring the small stellated dodecahedron is attributed to Uccello.
Piero della Francesca

Piero della Francesca
Piero della Francesca was a painter of the Early Renaissance. As testified by Giorgio Vasari in his Lives of the Artists, to contemporaries he was also known as a mathematician and geometer. Nowadays Piero della Francesca is chiefly appreciated for his art. His painting was characterized by its...
(c.1415-1492), an early Renaissance artist
Artist
An artist is a person engaged in one or more of any of a broad spectrum of activities related to creating art, practicing the arts and/or demonstrating an art. The common usage in both everyday speech and academic discourse is a practitioner in the visual arts only...
from Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
, exemplified this new shift in Renaissance thinking. Though chiefly appreciated for his art, he was an expert mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
and geometer and authored many books on solid geometry
Solid geometry
In mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...
and the emerging field of perspective
Perspective (graphical)
Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
, including De Prospectiva Pingendi (On Perspective for Painting), Trattato d’Abaco (Abacus Treatise), and De corporibus regularibus (Regular Solids). Historian Vasari in the Lives of the Painters calls Piero the “greatest geometer of his time, or perhaps of any time.” He was deeply interested in the theoretical study of perspective and this was apparent in many of his paintings, including the S. Agostino altarpiece and The Flagellation of Christ. His work on geometry influenced later mathematicians and artists, including Luca Pacioli
Luca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
in his De Divina Proportione and Leonardo da Vinci
Leonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
.
Piero began his study of classical mathematics and the works of the Greek mathematician Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in the library at Urbino
Urbino
Urbino is a walled city in the Marche region of Italy, south-west of Pesaro, a World Heritage Site notable for a remarkable historical legacy of independent Renaissance culture, especially under the patronage of Federico da Montefeltro, duke of Urbino from 1444 to 1482...
. In addition to this classical training, Piero was taught commercial arithmetic in “abacus schools,” evidenced indirectly by his own writings which copies the format of abacus school textbooks. It is possible therefore that he was influenced by the works of Leonardo Pisano (Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
) from which those abacus textbooks were derived. Piero lived in the time when linear perspective was just being introduced in the artistic world. Leon Battista Alberti sums up the idea: “light rays travel in straight lines from points in the observed scene to the eye, forming a kind of pyramid
Pyramid
A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...
with the eye as vertex.” The painting therefore is a cross-sectional
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
plane of that pyramid. The study of perspective precedes Piero and the Renaissance however. Before perspective, artists typically sized objects and figures according to their thematic importance. Perspective was first observed in 5th century B.C. Greece
Greece
Greece , officially the Hellenic Republic , and historically Hellas or the Republic of Greece in English, is a country in southeastern Europe....
and Euclid’s
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
Optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
first introduced a mathematical theory of perspective. Muslim mathematician Alhazen extended the theory of optics in his Book of Optics
Book of Optics
The Book of Optics ; ; Latin: De Aspectibus or Opticae Thesaurus: Alhazeni Arabis; Italian: Deli Aspecti) is a seven-volume treatise on optics and other fields of study composed by the medieval Muslim scholar Alhazen .-See also:* Science in medieval Islam...
in 1021 A.D., although he never applied these principals to art. Perspective first exploded onto the Renaissance artistic scene with Giotto di Bondone
Giotto di Bondone
Giotto di Bondone , better known simply as Giotto, was an Italian painter and architect from Florence in the late Middle Ages...
, who attempted to draw in perspective using an algebraic method to determine the placement of distant lines. In 1415, Italian architect
Architect
An architect is a person trained in the planning, design and oversight of the construction of buildings. To practice architecture means to offer or render services in connection with the design and construction of a building, or group of buildings and the space within the site surrounding the...
Filippo Brunelleschi
Filippo Brunelleschi
Filippo Brunelleschi was one of the foremost architects and engineers of the Italian Renaissance. He is perhaps most famous for inventing linear perspective and designing the dome of the Florence Cathedral, but his accomplishments also included bronze artwork, architecture , mathematics,...
and his friend Leon Battista Alberti demonstrated the geometrical method of applying perspective in Florence, centered around the usage of similar triangles, a mathematical concept formulated long ago by Euclid, in determining the apparent height of distant objects. However, Piero is the first painter to write a practical treatise for the application of this idea in art in his De Prospectiva Pingendi.

In Book I, after some elementary constructions to introduce the idea of the apparent size of an object being actually its angle subtended at the eye, and referring to Euclid's Elements Books I and VI, and Euclid's Optics, he turns, in Proposition 13, to the representation of a square lying flat on the ground in front of the viewer. What should the artist actually draw? After this, objects are constructed in the square (tilings, for example, to represent a tiled floor), and corresponding objects are constructed in perspective; in Book II prisms are erected over these planar objects, to represent houses, columns, etc.; but the basis of the method is the original square, from which everything else follows.
Notre Dame

In his 1919 book Ad Quadratum, Frederik Macody Lund
Frederik Macody Lund
thumb|Frederik Macody Lund Julius Frederik Macody Lund was a controversial Norwegian historian, most known and remembered for his engagement in the restoration of Nidaros Cathedral.When architect Christian Christie presented his ideas for a restoration of the west section and the west front, an...
, a historian who studied the geometry of several gothic structures, claims that the Cathedral of Chartres
Cathedral of Chartres
The French medieval Cathedral of Our Lady of Chartres is a Latin Rite Catholic cathedral located in Chartres, about southwest of Paris, is considered one of the finest examples of the French High Gothic style...
(begun in the 12th century), the Notre-Dame of Laon
Notre-Dame of Laon
Laon Cathedral is one of the most important examples of the Gothic architecture of the 12th and 13th centuries, earlier than the cathedrals of Sens and Notre Dame of Paris and ranking with them in importance. It is located in Laon, Picardy, France, and is the seat of the Bishop of Laon...
(1157–1205), and the Notre Dame de Paris
Notre Dame de Paris
Notre Dame de Paris , also known as Notre Dame Cathedral, is a Gothic, Roman Catholic cathedral on the eastern half of the Île de la Cité in the fourth arrondissement of Paris, France. It is the cathedral of the Catholic Archdiocese of Paris: that is, it is the church that contains the cathedra of...
(1160) are designed according to the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. According to Macody Lund, the superimposed regulator lines show that the cathedral has golden proportions. Other scholars argue that until Pacioli's 1509 publication, the golden ratio was unknown to artists and architects.
Albrecht Dürer

Albrecht Dürer
Albrecht Dürer was a German painter, printmaker, engraver, mathematician, and theorist from Nuremberg. His prints established his reputation across Europe when he was still in his twenties, and he has been conventionally regarded as the greatest artist of the Northern Renaissance ever since...
(1471–1528) was a German Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
printmaker who made important contributions to polyhedral literature in his book, Underweysung der Messung (Four Books on Measurement) (1525), meant to teach the subjects of linear perspective, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
in architecture
Architecture
Architecture is both the process and product of planning, designing and construction. Architectural works, in the material form of buildings, are often perceived as cultural and political symbols and as works of art...
, Platonic solids, and regular polygons. Dürer was likely influenced by the works of Luca Pacioli
Luca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
and Piero della Francesca
Piero della Francesca
Piero della Francesca was a painter of the Early Renaissance. As testified by Giorgio Vasari in his Lives of the Artists, to contemporaries he was also known as a mathematician and geometer. Nowadays Piero della Francesca is chiefly appreciated for his art. His painting was characterized by its...
during his trips to Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
. While the examples of perspective in Underweysung der Messung are underdeveloped and contain a number of inaccuracies, the manual does contain a very interesting discussion of polyhedra. Dürer is also the first to introduce in text the idea of polyhedral nets
Net (polyhedron)
In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...
, polyhedra unfolded to lie flat for printing. Dürer published another influential book on human proportions called Vier Bücher von Menschlicher Proportion (Four Books on Human Proportion) in 1528.
Dürer's well-known engraving Melancholia I depicts a frustrated thinker sitting by what is best interpreted as a “truncated rhomboid” or a “rhombohedron with 72-degree face angles, which has been truncated so it can be inscribed in a sphere”. It has been the subject of more modern interpretation than almost any other print, including a two-volume book by Peter-Klaus Schuster, and a very influential discussion in Erwin Panofsky
Erwin Panofsky
Erwin Panofsky was a German art historian, whose academic career was pursued mostly in the U.S. after the rise of the Nazi regime. Panofsky's work remains highly influential in the modern academic study of iconography...
's monograph of Dürer.
One might speculate that the cube represents masculinity and truncating one in an upright position may have some Freudian symbolism.
De Divina Proportione

Luca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
in Milan
Milan
Milan is the second-largest city in Italy and the capital city of the region of Lombardy and of the province of Milan. The city proper has a population of about 1.3 million, while its urban area, roughly coinciding with its administrative province and the bordering Province of Monza and Brianza ,...
from 1496–98, published in Venice
Venice
Venice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
in 1509, De Divina Proportione
De divina proportione
De Divina Proportione is a famous book on mathematics written by Luca Pacioli around 1497 in Milan. Today only two versions of the original manuscript are believed still to exist...
was about mathematical and artistic proportion. Leonardo da Vinci
Leonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
drew illustrations of regular solids in De divina proportione while he lived with and took mathematics lessons from Pacioli. Leonardo's drawings are probably the first illustrations of skeletonic solids, which allowed an easy distinction between front and back. Skeletonic solids, such as the rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
, were one of the first solids drawn to demonstrate perspective by being overlaid on top of each other. Additionally, the work also discusses the use of perspective by painters such as Piero della Francesca
Piero della Francesca
Piero della Francesca was a painter of the Early Renaissance. As testified by Giorgio Vasari in his Lives of the Artists, to contemporaries he was also known as a mathematician and geometer. Nowadays Piero della Francesca is chiefly appreciated for his art. His painting was characterized by its...
, Melozzo da Forlì
Melozzo da Forlì
Melozzo da Forlì was an Italian Renaissance painter and architect. His fresco paintings are notable for the use of foreshortening. He was the most important member of the Forlì painting school.- Biography :...
, and Marco Palmezzano
Marco Palmezzano
Marco Palmezzano was an Italian painter and architect, belonging to the Forlì painting school, who painted in a style recalling earlier Northern Renaissance models, and was mostly active near Forlì.-Biography:...
.
It is in De Divina Proportione that the golden ratio is defined as the divine proportion. Pacioli also details the use of the golden ratio as the mathematical definition of beauty when applied to the human face.
“The Ancients, having taken into consideration the rigorous construction of the human body, elaborated all their works, as especially their holy temples, according to these proportions; for they found here the two principal figures without which no project is possible: the perfection of the circle, the principle of all regular bodies, and the equilateral square.” from De Divina Proportione (1509)
Da Vinci

Leonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
(1452–1519) was an Italian scientist
Scientist
A scientist in a broad sense is one engaging in a systematic activity to acquire knowledge. In a more restricted sense, a scientist is an individual who uses the scientific method. The person may be an expert in one or more areas of science. This article focuses on the more restricted use of the word...
, mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, engineer
Engineer
An engineer is a professional practitioner of engineering, concerned with applying scientific knowledge, mathematics and ingenuity to develop solutions for technical problems. Engineers design materials, structures, machines and systems while considering the limitations imposed by practicality,...
, inventor, anatomist, painter
Painting
Painting is the practice of applying paint, pigment, color or other medium to a surface . The application of the medium is commonly applied to the base with a brush but other objects can be used. In art, the term painting describes both the act and the result of the action. However, painting is...
, sculptor, and architect
Architect
An architect is a person trained in the planning, design and oversight of the construction of buildings. To practice architecture means to offer or render services in connection with the design and construction of a building, or group of buildings and the space within the site surrounding the...
. Leonardo has often been described as the archetype of the Renaissance man.
Renowned primarily as a painter, Leonardo incorporated many mathematical concepts into his artwork despite never having received any formal mathematical training. It was not until the 1490s that he trained under Luca Pacioli
Luca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
and prepared a series of drawings for De Divina Proportione. Leonardo studied Pacioli's Summa, from which he copied tables of proportions and multiplication tables.
Notably in Mona Lisa and The Last Supper, Leonardo’s work incorporated the concept of linear perspective. By making all of the lines in the painting converge on a single, invisible point on the horizon, a flat painting can appear to have depth. In creating the vanishing point
Vanishing point
A vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used...
, Leonardo creates the illusion that the painting is an extension of the room itself.

Mona Lisa
Mona Lisa is a portrait by the Italian artist Leonardo da Vinci. It is a painting in oil on a poplar panel, completed circa 1503–1519...
, one can observe the mismatch between the left and right backgrounds which creates the illusion of perspective and depth. It is believed that Leonardo, as a mathematician, purposefully made this painting line up with Golden Rectangles in this fashion in order to further the incorporation of mathematics into art. A Golden Rectangle whose base extends from her right wrist to her left elbow and reaches the top of her very head can be constructed. This Golden Rectangle can be then further subdivided into smaller Golden Rectangles and can be drawn to produce the Golden Spiral. Also a viewer can note that all these edges of the new rectangles come to intersect the focal points of Mona Lisa: chin, eye, nose, and upturned corner of her mouth. It is also worth mentioning that the overall shape of the woman is a triangle with her arms as the base and her head as the tip. This is meant to draw attention to the face of the woman in the portrait.

In Vitruvian Man
Vitruvian Man
The Vitruvian Man is a world-renowned drawing created by Leonardo da Vinci circa 1487. It is accompanied by notes based on the work of the famed architect, Vitruvius. The drawing, which is in pen and ink on paper, depicts a male figure in two superimposed positions with his arms and legs apart and...
, Leonardo used both image and text to express the ideas and theories of Vitruvius
Vitruvius
Marcus Vitruvius Pollio was a Roman writer, architect and engineer, active in the 1st century BC. He is best known as the author of the multi-volume work De Architectura ....
, a first century Roman architect and author of De Architectura libri X. The Vitruvian ideas formed the basis of Renaissance proportion theories in art and architecture. Various artists and architects had illustrated Vitruvius' theory prior to Leonardo, but Leonardo's drawing differs from the previous works in that the male figure adopts two different positions within the same image. He is simultaneously within the circle and the square; movement and liveliness are suggested by the figure's active arms and legs.
The thin lines on his form show the significant points of the proportion scheme. These lines indicate Leonardo’s concern with the architectural meaning of the work. Leonardo is representing the body as a building and illustrating Renaissance theory which linked the proportions of the human body with architectural planning.
Penrose tiles
.svg.png)
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
due to its nonperiodicity, and any finite region in a tiling appears infinitely many times in the tiling.
Both visually complex and simple at the same time, Penrose tiles arise from basic mathematical principles and can be viewed as intricately related to the golden ratio. Two notable relationships between Penrose tiles and the Golden ratio are:
- The ratio of thick to thin rhombuses in the infinite tile is the golden ratio 1.618.
- The distances between repeated patterns in the tiling grow as Fibonacci numbers when the size of the repetition increases.
Eden Project
Located near St. Austell in Southwestern England, the Eden Project has intricate greenhouses composed of geodesic domes (also known as biomes). Known to many as a visitor attraction with the world’s largest greenhouse, the Eden Project is a dedication to preserving nature and the mathematics embedded in nature’s design. Throughout the center visitors can notice intricate patterning of pentagons and hexagons that form unique architectural structures mimicking nature’s simple and complex shapes. Additionally, the Eden Project biomes house plant species from around the world with each honeycomb like dome emulating a natural environment.The Core, a new education building, was constructed with the inspiration of the Fibonacci Numbers and plant spirals. From a top down view, one can see the building’s windows aligned in a spiral similar to the golden spiral
Golden spiral
In geometry, a golden spiral is a logarithmic spiral whose growth factor is , the golden ratio. That is, a golden spiral gets wider by a factor of for every quarter turn it makes.-Formula:...
and plant spirals.
California Polytechnic State University
Like many college campuses throughout the country trying to inspire its students, the Engineering Plaza of California Polytechnic State University was designed to incorporate the Fibonacci sequence and golden spiralGolden spiral
In geometry, a golden spiral is a logarithmic spiral whose growth factor is , the golden ratio. That is, a golden spiral gets wider by a factor of for every quarter turn it makes.-Formula:...
. Campus buildings were designed around the concept of the golden spiral which is defined at the very center by the three core buildings. The outward spiraling arc can be seen below and extends throughout the campus.
M.C. Escher

Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
s, and translations
Translations
Translations is a three-act play by Irish playwright Brian Friel written in 1980. It is set in Baile Beag , a small village at the heart of 19th century agricultural Ireland...
to obtain many more patterns. Additionally, Escher arranged the shapes to simulate images of animals and other figures.
His work can be noted in Development 1 and Cycles.
Escher’s was also interested in a specific type of polyhedron that appears many times in his work. These polyhedrons are defined as solids that have exactly similar polygonal faces, also known as Platonic solids. These Platonic solids, tetrahedrons, cubes, octahedrons, dodecahedrons, and icosahedrons stellations are especially prominent in Order and Chaos and Four Regular Solids. Here these stellated figures often reside within another figure which further distorts the viewing angle and conformation of the polyhedrons and providing a multifaceted perspective artwork.
Additionally, Escher worked with the shape and logic of space in Three Intersecting Planes, Snakes
Snakes (M. C. Escher)
Snakes is a woodcut print by the Dutch artist M. C. Escher which was first printed in July 1969.It depicts a disc made up of interlocking circles which grow progressively smaller towards the center and towards the edge...
, High and Low, and Waterfall
Waterfall (M. C. Escher)
Waterfall is a lithography print by the Dutch artist M. C. Escher which was first printed in October, 1961. It shows an apparent paradox where water from the base of a waterfall appears to run downhill before reaching the top of the waterfall....
.
Many of Escher's works contain impossible constructions, made using geometrical objects that cannot exist but are pleasant to the human sight. Some of Escher's tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
drawings were inspired by conversations with the mathematician H. S. M. Coxeter concerning hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. Relationships between the works of mathematician Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
, artist M. C. Escher
M. C. Escher
Maurits Cornelis Escher , usually referred to as M. C. Escher , was a Dutch graphic artist. He is known for his often mathematically inspired woodcuts, lithographs, and mezzotints...
and composer Johann Sebastian Bach
Johann Sebastian Bach
Johann Sebastian Bach was a German composer, organist, harpsichordist, violist, and violinist whose sacred and secular works for choir, orchestra, and solo instruments drew together the strands of the Baroque period and brought it to its ultimate maturity...
are explored in Gödel, Escher, Bach
Gödel, Escher, Bach
Gödel, Escher, Bach: An Eternal Golden Braid is a book by Douglas Hofstadter, described by his publishing company as "a metaphorical fugue on minds and machines in the spirit of Lewis Carroll"....
, a Pulitzer Prize
Pulitzer Prize
The Pulitzer Prize is a U.S. award for achievements in newspaper and online journalism, literature and musical composition. It was established by American publisher Joseph Pulitzer and is administered by Columbia University in New York City...
-winning book.
Salvador Dali

Crucifixion (Corpus Hypercubus)
Crucifixion was painted in 1954 by Salvador Dalí, and depicts the crucified Jesus upon the net of a hypercube. Gala , is the figure in the bottom left, who stands looking up to the crucified Jesus. The scene is depicted in front of the bay of Port Lligat.The painting is in the Metropolitan Museum...
depicts a crucified figure upon the net of a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
. In The Sacrament of the Last Supper
The Sacrament of the Last Supper
Completed in 1955 after nine months of work, Salvador Dalí’s painting The Sacrament of the Last Supper has remained one of his most popular compositions. Since its arrival at the National Gallery of Art in Washington, D.C...
(1955) Christ and his disciples are pictured inside a giant dodecahedron. Dali's last painting, The Swallow's Tail
The Swallow's Tail
The Swallow's Tail — Series on Catastrophes was Salvador Dalí's last painting. It was completed in May 1983, as the final part of a series based on René Thom's catastrophe theory....
(1983), was part of a series inspired by René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
's catastrophe theory
Catastrophe theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry....
.
Pablo Palazuelo
Pablo PalazueloPablo Palazuelo
Pablo Palazuelo was a Spanish painter and sculptor.- Work and Biography :Pablo Palazuelo was born in Madrid in 1916. In 1933 he studied architecture at the School of Arts and Crafts at Oxford University. Upon returning to Madrid in 1939, he began to devote all of his time to painting...
(1969–2007) was a contemporary Spanish painter and sculptor focused on the investigation of form. Heavily influenced by cubism and Paul Klee, Palazuelo developed a unique style that he described as the geometry of life and the geometry of all nature. Consisting of simple geometric shapes with detailed patterning and coloring, Palazuelo’s work was noted as powerful, attractive, unhesitant, enigmatic, and always new. From works such as Angular I to Automnes, Palazuelo expressed himself in geometric transformations and translations. Over time as Carmen Bonell notes, Palazuelo’s work evolved very rapidly toward an abstract-geometric language of increasing purity.
John Robinson
John RobinsonJohn Robinson (sculptor)
John Robinson was a British sculptor and co-founder of the . Accounts of his work may be seen at the , the website of the and the June and July 2007, issues of...
(1935–2007) was originally a sheep farmer who turned to sculpting. He began a serious sculpting career at the age of 35. Robinson was deeply interested in astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and mathematical relationships. According to Ronald Brown, Robinson’s work was extraordinary because of its proportion, line, rhythm, finish, the resonance of the titles and the forms, and because some of the complex forms, such as Rhythm of Life, had hardly been visualized in such an exact way. Robinson’s work from Gordian Knot to Bands of Friendship displayed highly complex mathematical knot theory in polished bronze for the public to see.
Many mathematicians working in the field of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and specifically with torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
es see mathematical relationships in Robinson’s sculptures.
Rhythm of Life arose from experiments with wrapping a ribbon around an inner tube and finding it returned to itself.
Genesis evolved from an attempt at making Borromean rings-a set of three circles, no two of which link but in which the whole structure cannot be taken apart without breaking.
Many of Robinson’s works express the theme of common humanity. In Dependent Beings, the sculpture comprises a square that twists as it travels around the circle, giving it a boundary of two strips in contrasting textures.
The Eightfold Way
Sculptor Helaman FergusonHelaman Ferguson
Helaman Rolfe Pratt Ferguson is an American sculptor and a digital artist, specifically an algorist.Ferguson's mother died when he was about three and his father went off to serve in the Second World War. He was adopted and raised in New York. He was a graduate of Hamilton College and received a...
has made sculptures in various materials of a wide range of complex surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s and other topological objects
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. His work is motivated specifically by the desire to create visual representations of mathematical objects.
Ferguson has created a sculpture called The Eightfold Way at the Berkeley, California, Mathematical Sciences Research Institute based on the projective special linear group PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
, a finite group of 168 elements.
Fractal art

The processing power of modern computers allows mathematicians and non-mathematicians to visualise complex mathematical objects such as the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
. In the modern industry of computer animation
Computer animation
Computer animation is the process used for generating animated images by using computer graphics. The more general term computer generated imagery encompasses both static scenes and dynamic images, while computer animation only refers to moving images....
, fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s play a key role in modelling mountains, fire, trees and other natural objects.
Platonic solids in art
The Platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s and other polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
are a recurring theme in Western art. Examples include:
- A marble mosaic featuring the small stellated dodecahedron, attributed to Paolo UccelloPaolo UccelloPaolo Uccello , born Paolo di Dono, was an Italian painter and a mathematician who was notable for his pioneering work on visual perspective in art. Giorgio Vasari in his book Lives of the Artists wrote that Uccello was obsessed by his interest in perspective and would stay up all night in his...
, in the floor of the San Marco Basilica in Venice. - Leonardo da VinciLeonardo da VinciLeonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
's outstanding diagrams of regular polyhedra drawn as illustrations for Luca PacioliLuca PacioliFra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
's book The Divine Proportion. - A glass rhombicuboctahedronRhombicuboctahedronIn geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
in Jacopo de Barbari's portrait of Pacioli, painted in 1495. - A truncated polyhedron (and various other mathematical objects) which feature in Albrecht DürerAlbrecht DürerAlbrecht Dürer was a German painter, printmaker, engraver, mathematician, and theorist from Nuremberg. His prints established his reputation across Europe when he was still in his twenties, and he has been conventionally regarded as the greatest artist of the Northern Renaissance ever since...
's engraving Melancholia I. - Salvador DalíSalvador DalíSalvador Domènec Felip Jacint Dalí i Domènech, Marquis de Púbol , commonly known as Salvador Dalí , was a prominent Spanish Catalan surrealist painter born in Figueres,Spain....
's painting The Last Supper in which Christ and his disciples are pictured inside a giant dodecahedron.
Bridges conference
The Bridges Organization organise a yearly conference on the connections between maths and art. The conferences features work of many contemporary mathematically inspired artists.See also
- George W. HartGeorge W. HartGeorge William Hart is a geometer who expresses himself both artistically and academically. He is also a research professor in the department of computer science at the State University of New York in Stony Brook, New York....
- Mathematics and architectureMathematics and architectureMathematics and architecture have always been close, not only because architecture depends on developments in mathematics, but also their shared search for order and beauty, the former in nature and the latter in construction. Mathematics is indispensable to the understanding of structural concepts...
- Mathematics of musical scales
- Maurice PrincetMaurice PrincetMaurice Princet was a French mathematician and actuary who played a role in the birth of cubism. He was an associate of Pablo Picasso, Guillaume Apollinaire, Max Jacob, Jean Metzinger, and Marcel Duchamp...
External links
- Connections in Space - topology in art
- Mathematics and Art at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- National University of Singapore's course on Mathematics in Art and Architecture
- Mathematical Imagery presented by the American Mathematical SocietyAmerican Mathematical SocietyThe American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...

