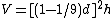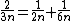Rhind Mathematical Papyrus
Encyclopedia
The Rhind Mathematical Papyrus (RMP) (also designated as: papyrus British Museum
10057, and pBM 10058), is named after Alexander Henry Rhind
, a Scottish
antiquarian, who purchased the papyrus
in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum
. It dates to around 1650 BC. The British Museum, where the papyrus is now kept, acquired it in 1864 along with the Egyptian Mathematical Leather Roll
, also owned by Henry Rhind; there are a few small fragments held by the Brooklyn Museum
in New York
. It is one of the two well-known Mathematical Papyri along with the Moscow Mathematical Papyrus
. The Rhind Papyrus is larger than the Moscow Mathematical Papyrus, while the latter is older than the former.
The Rhind Mathematical Papyrus dates to the Second Intermediate Period of Egypt
and is the best example of Egyptian mathematics
. It was copied by the scribe Ahmes
(i.e., Ahmose; Ahmes is an older transcription
favoured by historians of mathematics), from a now-lost text from the reign of king
Amenemhat III
(12th dynasty
). Written in the hieratic
script, this Egyptian manuscript
is 33 cm tall and just under 2 m long, and began to be transliterated and mathematically translated in the late 19th century. In 2008, the mathematical translation aspect is incomplete in several respects. The document is dated to Year 33 of the Hyksos
king Apophis
and also contains a separate later Year 11 on its verso likely from his successor, Khamudi
.
In the opening paragraphs of the papyrus, Ahmes presents the papyrus as giving "Accurate reckoning for inquiring into things, and the knowledge of all things, mysteries...all secrets". He continues with:
Several books and articles about the Rhind Mathematical Papyrus have been published, and a handful of these stand out. The Rhind Papyrus was published in 1923 by Peet and contains a discussion of the text that followed Griffith's Book I, II and III outline Chase published a compendium in 1927/29 which included photographs of the text. A more recent overview of the Rhind Papyrus was published in 1987 by Robins and Shute.
The first part of the papyrus is taken up by the 2/n table
. The fractions 2/n for odd n ranging from 3 to 101 are expressed as sums of unit fractions. For example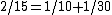 . The decomposition of 2/n into unit fractions is never more than 4 terms long as in for example
. The decomposition of 2/n into unit fractions is never more than 4 terms long as in for example 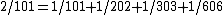 .
.
This table is followed by a list of fraction expressions for the numbers 1 through 9 divided by 10. For instance the division of 7 by 10 is recorded as:
After these two tables, the scribe recorded 84 problems altogether and problems 1 through 40 which belong to Book I are of an algebraic nature.
Problems 1–6 compute divisions of a certain number of loaves of bread by 10 men and record the outcome in unit fractions. Problems 7–20 show how to multiply the expressions 1 + 1/2 + 1/4 and 1 + 2/3 + 1/3 by different fractions.
Problems 21–23 are problems in completion, which in modern notation is simply a subtraction problem. The problem is solved by the scribe to multiply the entire problem by a least common multiple
of the denominators, solving the problem and then turning the values back into fractions. Problems 24–34 are ‘’aha’’ problems. These are linear equations. Problem 32 for instance corresponds (in modern notation) to solving x + 1/3 x + 1/4 x = 2 for x. Problems 35–38 involve divisions of the hekat. Problems 39 and 40 compute the division of loaves and use arithmetic progressions.
.png) The second part of the Rhind papyrus consists of geometry
The second part of the Rhind papyrus consists of geometry
problems. Peet referred to these problems as "mensuration problems".
In modern mathematical notation (and using d = 2r) this clearly equals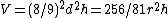 The quotient 256/81 approximates the value of π as being ca. 3.1605.
The quotient 256/81 approximates the value of π as being ca. 3.1605.
In problem 42 the scribe uses a slightly different formula which computes the volume and expresses it in terms of the unit khar.
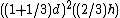 In modern mathematical notation this is equal to
In modern mathematical notation this is equal to 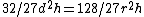 (measured in khar).
(measured in khar).
This is equivalent to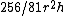 measured in cubic-cubits as used in the other problem.
measured in cubic-cubits as used in the other problem.
Problem 47 gives a table with equivalent fractions for fractions of 100 quadruple hekat of grain. The quotients are expressed in terms of Horus eye fractions. The short table gives the values related to the original 100 quadruple hekat:
. Problem 48 is often commented on as it computes the area of a circle. The scribe compares the area of a circle (approximated by an octagon) and its circumscribing square. Each side is trisected and the corner triangles are then removed. The resulting octagonal figure approximates the circle. The area of the octagonal figure is: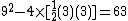 ; Next we approximate 63 to be 64 and note that
; Next we approximate 63 to be 64 and note that 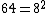 . And we get the approximation
. And we get the approximation 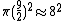 . Solving for π, we get the approximation
. Solving for π, we get the approximation 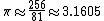 (the approximation has an error of .0189).
(the approximation has an error of .0189).
That this octagonal figure, whose area is easily calculated, so accurately approximates the area of the circle is just plain good luck. Obtaining a better approximation to the area using finer divisions of a square and a similar argument is not simple.
Other problems show how to find the area of rectangles, triangles and trapezoids.
s.
A seked
problem is reported by :
The solution to the problem is given as the ratio of half the side of the base of the pyramid to its height, or the run-to-rise ratio of its face. In other words, the quantity he found for the seked is the cotangent of the angle to the base of the pyramid and its face.
Problem 61 consists of 2 parts. Part 1 contains multiplications of fractions. Part b gives a general expression for computing 2/3 of 1/n, where n is odd. In modern notation the formula given is
Problems 62- 68 are general problems of an algebraic nature. Problems 69 - 78 are all pefsu problems in some form or another. They involve computations regarding the strength of bread and or beer.
Problem RMP 79' sums five terms in a geometric progression
. It is a multiple of 7 riddle, which would have been written in the Medieval era as, "Going to St. Ives
" problem.
Problems 80 and 81 compute Horus eye fractions of henu (or hekats). Problem 81 is followed by a table. The last three problems 82 - 84 compute the amount of feed necessary for fowl and oxen.
British Museum
The British Museum is a museum of human history and culture in London. Its collections, which number more than seven million objects, are amongst the largest and most comprehensive in the world and originate from all continents, illustrating and documenting the story of human culture from its...
10057, and pBM 10058), is named after Alexander Henry Rhind
Alexander Henry Rhind
Alexander Henry Rhind was a Scottish lawyer and Egyptologist.Born in Wick on 26 July 1833 in the Highlands, Rhind studied at the University of Edinburgh...
, a Scottish
Scotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
antiquarian, who purchased the papyrus
Papyrus
Papyrus is a thick paper-like material produced from the pith of the papyrus plant, Cyperus papyrus, a wetland sedge that was once abundant in the Nile Delta of Egypt....
in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum
Ramesseum
The Ramesseum is the memorial temple of Pharaoh Ramesses II . It is located in the Theban necropolis in Upper Egypt, across the River Nile from the modern city of Luxor...
. It dates to around 1650 BC. The British Museum, where the papyrus is now kept, acquired it in 1864 along with the Egyptian Mathematical Leather Roll
Egyptian Mathematical Leather Roll
The Egyptian Mathematical Leather Roll was a 10 × 17 in leather roll purchased by Alexander Henry Rhind in 1858...
, also owned by Henry Rhind; there are a few small fragments held by the Brooklyn Museum
Brooklyn Museum
The Brooklyn Museum is an encyclopedia art museum located in the New York City borough of Brooklyn. At 560,000 square feet, the museum holds New York City's second largest art collection with roughly 1.5 million works....
in New York
New York
New York is a state in the Northeastern region of the United States. It is the nation's third most populous state. New York is bordered by New Jersey and Pennsylvania to the south, and by Connecticut, Massachusetts and Vermont to the east...
. It is one of the two well-known Mathematical Papyri along with the Moscow Mathematical Papyrus
Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
. The Rhind Papyrus is larger than the Moscow Mathematical Papyrus, while the latter is older than the former.
The Rhind Mathematical Papyrus dates to the Second Intermediate Period of Egypt
History of Ancient Egypt
The History of Ancient Egypt spans the period from the early predynastic settlements of the northern Nile Valley to the Roman conquest in 30 BC...
and is the best example of Egyptian mathematics
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
. It was copied by the scribe Ahmes
Ahmes
Ahmes was an ancient Egyptian scribe who lived during the Second Intermediate Period and the beginning of the Eighteenth Dynasty . He wrote the Rhind Mathematical Papyrus, a work of Ancient Egyptian mathematics that dates to approximately 1650 BC; he is the earliest contributor to mathematics...
(i.e., Ahmose; Ahmes is an older transcription
Transcription (linguistics)
Transcription in the linguistic sense is the systematic representation of language in written form. The source can either be utterances or preexisting text in another writing system, although some linguists only consider the former as transcription.Transcription should not be confused with...
favoured by historians of mathematics), from a now-lost text from the reign of king
Pharaoh
Pharaoh is a title used in many modern discussions of the ancient Egyptian rulers of all periods. The title originates in the term "pr-aa" which means "great house" and describes the royal palace...
Amenemhat III
Amenemhat III
Amenemhat III, also spelled Amenemhet III was a pharaoh of the Twelfth Dynasty of Egypt. He ruled from c.1860 BC to c.1814 BC, the latest known date being found in a papyrus dated to Regnal Year 46, I Akhet 22 of his rule. He is regarded as the greatest monarch of the Middle Kingdom...
(12th dynasty
Twelfth dynasty of Egypt
The twelfth dynasty of ancient Egypt is often combined with Dynasties XI, XIII and XIV under the group title Middle Kingdom.-Rulers:Known rulers of the twelfth dynasty are as follows :...
). Written in the hieratic
Hieratic
Hieratic refers to a cursive writing system that was used in the provenance of the pharaohs in Egypt and Nubia that developed alongside the hieroglyphic system, to which it is intimately related...
script, this Egyptian manuscript
Manuscript
A manuscript or handwrite is written information that has been manually created by someone or some people, such as a hand-written letter, as opposed to being printed or reproduced some other way...
is 33 cm tall and just under 2 m long, and began to be transliterated and mathematically translated in the late 19th century. In 2008, the mathematical translation aspect is incomplete in several respects. The document is dated to Year 33 of the Hyksos
Hyksos
The Hyksos were an Asiatic people who took over the eastern Nile Delta during the twelfth dynasty, initiating the Second Intermediate Period of ancient Egypt....
king Apophis
Apepi I
Apepi or Apophis was a ruler of Lower Egypt during the fifteenth dynasty and the end of the Second Intermediate Period that was dominated by this foreign dynasty of rulers called the Hyksos...
and also contains a separate later Year 11 on its verso likely from his successor, Khamudi
Khamudi
Khamudi was the last pharaoh of the Hyksos fifteenth dynasty of Egypt, who came to power in the northern portion of Egypt...
.
In the opening paragraphs of the papyrus, Ahmes presents the papyrus as giving "Accurate reckoning for inquiring into things, and the knowledge of all things, mysteries...all secrets". He continues with:
This book was copied in regnal year 33, month 4 of Akhet, under the majesty of the King of Upper and Lower Egypt, Awserre, given life, from an ancient copy made in the time of the King of Upper and Lower Egypt Nimaatre (?). The scribe Ahmose writes this copy.
Several books and articles about the Rhind Mathematical Papyrus have been published, and a handful of these stand out. The Rhind Papyrus was published in 1923 by Peet and contains a discussion of the text that followed Griffith's Book I, II and III outline Chase published a compendium in 1927/29 which included photographs of the text. A more recent overview of the Rhind Papyrus was published in 1987 by Robins and Shute.
Book I
The first part of the Rhind papyrus consists of reference tables and a collection of 20 arithmetic and 20 algebraic problems. The problems start out with simple fractional expressions, followed by completion (sekhem) problems and more involved linear equations (aha problems).The first part of the papyrus is taken up by the 2/n table
Rhind Mathematical Papyrus 2/n table
The Rhind Mathematical Papyrus contains, among other mathematical contents, a table of Egyptian fractions created from 2/n. The text reports 51 rational numbers converted to concise unit fraction series. The document was written in 1650 BCE by Ahmes...
. The fractions 2/n for odd n ranging from 3 to 101 are expressed as sums of unit fractions. For example
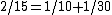 . The decomposition of 2/n into unit fractions is never more than 4 terms long as in for example
. The decomposition of 2/n into unit fractions is never more than 4 terms long as in for example 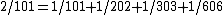 .
.This table is followed by a list of fraction expressions for the numbers 1 through 9 divided by 10. For instance the division of 7 by 10 is recorded as:
- 7 divided by 10 yields 2/3 + 1/30
After these two tables, the scribe recorded 84 problems altogether and problems 1 through 40 which belong to Book I are of an algebraic nature.
Problems 1–6 compute divisions of a certain number of loaves of bread by 10 men and record the outcome in unit fractions. Problems 7–20 show how to multiply the expressions 1 + 1/2 + 1/4 and 1 + 2/3 + 1/3 by different fractions.
Problems 21–23 are problems in completion, which in modern notation is simply a subtraction problem. The problem is solved by the scribe to multiply the entire problem by a least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of the denominators, solving the problem and then turning the values back into fractions. Problems 24–34 are ‘’aha’’ problems. These are linear equations. Problem 32 for instance corresponds (in modern notation) to solving x + 1/3 x + 1/4 x = 2 for x. Problems 35–38 involve divisions of the hekat. Problems 39 and 40 compute the division of loaves and use arithmetic progressions.
Book II
.png)
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
problems. Peet referred to these problems as "mensuration problems".
Volumes
Problems 41 – 46 show how to find the volume of both cylindrical and rectangular based granaries. In problem 41 the scribe computes the volume of a cylindrical granary. Given the diameter (d) and the height (h), the volume V is given by:In modern mathematical notation (and using d = 2r) this clearly equals
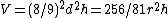 The quotient 256/81 approximates the value of π as being ca. 3.1605.
The quotient 256/81 approximates the value of π as being ca. 3.1605.In problem 42 the scribe uses a slightly different formula which computes the volume and expresses it in terms of the unit khar.
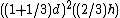 In modern mathematical notation this is equal to
In modern mathematical notation this is equal to 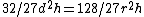 (measured in khar).
(measured in khar).This is equivalent to
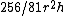 measured in cubic-cubits as used in the other problem.
measured in cubic-cubits as used in the other problem. Problem 47 gives a table with equivalent fractions for fractions of 100 quadruple hekat of grain. The quotients are expressed in terms of Horus eye fractions. The short table gives the values related to the original 100 quadruple hekat:
- 1/10 gives 10 quadruple hekat
- 1/20 gives 5 quadruple hekat
- 1/30 gives 3 1/4 1/16 1/64 (quadruple) hekat and 1 2/3 ro
- 1/40 gives 2 1/2 (quadruple) hekat
- 1/50 gives 2 (quadruple) hekat
- 1/60 gives 1 1/2 1/8 1/32 (quadruple) hekat 3 1/3 ro
- 1/70 gives 1 1/4 1/8 1/32 1/64 (quadruple) hekat 2 1/14 1/21 ro
- 1/80 gives 1 1/4 (quadruple) hekat
- 1/90 gives 1 1/16 1/32 1/64 (quadruple) hekat 1/2 1/18 ro
- 1/100 gives 1 (quadruple) hekat
Areas
Problems 48 - 55 show how to compute an assortment of areasArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
. Problem 48 is often commented on as it computes the area of a circle. The scribe compares the area of a circle (approximated by an octagon) and its circumscribing square. Each side is trisected and the corner triangles are then removed. The resulting octagonal figure approximates the circle. The area of the octagonal figure is:
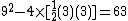 ; Next we approximate 63 to be 64 and note that
; Next we approximate 63 to be 64 and note that 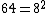 . And we get the approximation
. And we get the approximation 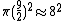 . Solving for π, we get the approximation
. Solving for π, we get the approximation 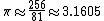 (the approximation has an error of .0189).
(the approximation has an error of .0189).That this octagonal figure, whose area is easily calculated, so accurately approximates the area of the circle is just plain good luck. Obtaining a better approximation to the area using finer divisions of a square and a similar argument is not simple.
Other problems show how to find the area of rectangles, triangles and trapezoids.
Pyramids
The final five problems are related to the slopes of pyramidPyramid
A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...
s.
A seked
Seked
The seked was an ancient Egyptian unit for the measurement of the slope of an inclined surface. The system was based on the Egyptian's linear measure known as the royal cubit. The royal cubit was subdivided into seven palms and each palm was further divided into four digits...
problem is reported by :
- If a pyramid is 250 cubits high and the side of its base 360 cubits long, what is its seked?"
The solution to the problem is given as the ratio of half the side of the base of the pyramid to its height, or the run-to-rise ratio of its face. In other words, the quantity he found for the seked is the cotangent of the angle to the base of the pyramid and its face.
Book III
The third part of the Rhind papyrus consists of a collection of 24 problems.Problem 61 consists of 2 parts. Part 1 contains multiplications of fractions. Part b gives a general expression for computing 2/3 of 1/n, where n is odd. In modern notation the formula given is
Problems 62- 68 are general problems of an algebraic nature. Problems 69 - 78 are all pefsu problems in some form or another. They involve computations regarding the strength of bread and or beer.
Problem RMP 79' sums five terms in a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
. It is a multiple of 7 riddle, which would have been written in the Medieval era as, "Going to St. Ives
As I Was Going to St Ives
"As I was going to St Ives" is a traditional English language nursery rhyme which is generally thought to be a riddle. It has a Roud Folk Song Index number of 19772.-Lyrics:The most common modern version is:-Answers:...
" problem.
Problems 80 and 81 compute Horus eye fractions of henu (or hekats). Problem 81 is followed by a table. The last three problems 82 - 84 compute the amount of feed necessary for fowl and oxen.
See also
- Lahun Mathematical PapyriLahun Mathematical PapyriThe Lahun Mathematical Papyri are part of a collection of Kahun Papyri discovered at El-Lahun by Flinders Petrie during excavations of a worker's town near the pyramid of Sesostris II...
- Akhmim wooden tabletAkhmim wooden tabletThe Akhmim wooden tablets or Cairo wooden tablets are two ancient Egyptian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed...
- Berlin PapyrusBerlin papyrusThe Berlin Papyrus 6619, commonly known as the Berlin Papyrus, is an ancient Egyptian papyrus document from the Middle Kingdom. This papyrus was found at the ancient burial ground of Saqqara in the early 19th century CE....
also known as Berlin Papyrus 6619 - Rhind Mathematical Papyrus 2/n tableRhind Mathematical Papyrus 2/n tableThe Rhind Mathematical Papyrus contains, among other mathematical contents, a table of Egyptian fractions created from 2/n. The text reports 51 rational numbers converted to concise unit fraction series. The document was written in 1650 BCE by Ahmes...
Further reading
- Gillings, Richard J. "Mathematics in the Time of the Pharaohs", 1972, MIT Press, Dover reprint ISBN 0-486-24315-X
External links
- Allen, Don. April 2001. The Ahmes Papyrus and Summary of Egyptian Mathematics.
- British Museum webpage on the Papyrus.
- O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri.
- Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: The Rhind/Ahmes Papyrus.
- Williams, Scott W. Mathematicians of the African Diaspora, containing a page on Egyptian Mathematics Papyri.
- BBC audio file A History of the World in 100 ObjectsA History of the World in 100 ObjectsA History of the World in 100 Objects was a joint project of BBC Radio 4 and the British Museum, comprising a 100-part radio series written and presented by British Museum director Neil MacGregor...
. (15 mins)