Polyhedron
Encyclopedia
|
In elementary geometry a polyhedron (plural polyhedra or polyhedrons) is a geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
solid in three dimensions
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
with flat faces and straight edges. The word polyhedron comes from the Classical Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
πολύεδρον, as poly- (stem of πολύς, "many") + -hedron (form of έδρα, "base", "seat", or "face").
A polyhedron is a 3-dimensional example of the more general polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
in any number of dimensions.
Basis for definition
Defining a polyhedron as a solid bounded by flat faces and straight edges is not very precise and, to a modern mathematician, quite unsatisfactory. GrünbaumBranko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
(1994, p. 43) observed, "The Original Sin
Original sin
Original sin is, according to a Christian theological doctrine, humanity's state of sin resulting from the Fall of Man. This condition has been characterized in many ways, ranging from something as insignificant as a slight deficiency, or a tendency toward sin yet without collective guilt, referred...
in the theory of polyhedra goes back to Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, and through Kepler, Poinsot, Cauchy and many others ... [in that] at each stage ... the writers failed to define what are the 'polyhedra' ...." Since then rigorous definitions of "polyhedron" have been given within particular contexts. However such definitions are not always compatible in other contexts.
Any polyhedron can be built up from different kinds of element or entity, each associated with a different number of dimensions:
- 3 dimensions: The body is bounded by the faces, and is usually the volume enclosed by them.
- 2 dimensions: A faceFace (geometry)In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
is a polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
bounded by a circuit of edges, and usually including the flat (plane) region inside the boundary. These polygonal faces together make up the polyhedral surface. - 1 dimension: An edgeEdge (geometry)In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
joins one vertex to another and one face to another, and is usually a lineLine (mathematics)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
segment. The edges together make up the polyhedral skeleton. - 0 dimensions: A vertexVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
(plural vertices) is a corner pointPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. - -1 dimension: The null polytope is a kind of non-entity required by abstract theories.
More generally in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and other disciplines, "polyhedron" is used to refer to a variety of related constructs, some geometric and others purely algebraic or abstract.
Polyhedral surface
A defining characteristic of almost all kinds of polyhedra is that just two faces join along any common edge. This ensures that the polyhedral surface is continuously connected and does not end abruptly or split off in different directions.Edges
Edges have two important characteristics (unless the polyhedron is complex):- An edge joins just two vertices.
- An edge joins just two faces.
These two characteristics are dual to each other.
Euler characteristic
The Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
χ relates the number of vertices V, edges E, and faces F of a polyhedron:
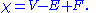
For a convex polyhedron or more generally for any simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
polyhedron whose faces are also simply connected and whose boundary is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, χ = 2. For a detailed discussion, see Proofs and Refutations
Proofs and Refutations
Proofs and Refutations is a book by the philosopher Imre Lakatos expounding his view ofthe progress of mathematics. The book is written as a series of Socratic dialogues involving a group of students who debate the proof of the Euler characteristic defined for the polyhedron...
by Imre Lakatos
Imre Lakatos
Imre Lakatos was a Hungarian philosopher of mathematics and science, known for his thesis of the fallibility of mathematics and its 'methodology of proofs and refutations' in its pre-axiomatic stages of development, and also for introducing the concept of the 'research programme' in his...
.
Orientability
Some polyhedra, such as all convex polyhedraConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
, have two distinct sides to their surface, for example one side can consistently be coloured black and the other white. We say that the figure is orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
.
But for some polyhedra this is not possible, and the figure is said to be non-orientable. All polyhedra with odd-numbered Euler characteristic are non-orientable. A given figure with even χ < 2 may or may not be orientable.
Vertex figure
For every vertex one can define a vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, which describes the local structure of the figure around the vertex. If the vertex figure is a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
, then the vertex itself is said to be regular.
Duality
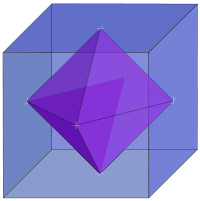
For every polyhedron there exists a dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
having:
- faces in place of the original's vertices and vice versa,
- the same number of edges
- the same Euler characteristic and orientability
The dual of a convex polyhedron can be obtained by the process of polar reciprocation.
Volume
The volume of an orientableOrientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
polyhedron can be calculated using the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
. Consider the vector field
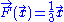 , whose divergence is identically 1. The divergence theorem implies that the volume of any region Ω is
, whose divergence is identically 1. The divergence theorem implies that the volume of any region Ω is
When Ω is the region enclosed by a polyhedron, since the faces of a polyhedron are planar and have piecewise constant normals, this simplifies to
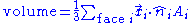
where for the ith face,
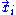 is any point on the face,
is any point on the face, 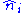 is the normal vector, and
is the normal vector, and 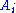 is area of the face.
is area of the face.Names of polyhedra
Polyhedra are often named according to the number of faces. The naming system is again based on Classical Greek, for example tetrahedronTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(4), pentahedron
Pentahedron
In geometry, a pentahedron is a polyhedron with five faces. Since there are no face-transitive polyhedra with five sides and there are two distinct topological types, this term is less frequently used than tetrahedron or octahedron....
(5), hexahedron
Hexahedron
A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....
(6), heptahedron
Heptahedron
A heptahedron is a polyhedron having seven sides, or faces.A heptahedron can take a surprising number of different basic forms, or topologies. Probably most familiar are the hexagonal pyramid and the pentagonal prism. Also notable is the tetrahemihexahedron, whose seven equilateral triangle faces...
(7), triacontahedron (30), and so on.
Often this is qualified by a description of the kinds of faces present, for example the Rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
vs. the Pentagonal dodecahedron.
Other common names indicate that some operation has been performed on a simpler polyhedron, for example the truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
looks like a cube with its corners cut off, and has 14 faces (so it is also an example of a tetrakaidecahedron).
Some special polyhedra have grown their own names over the years, such as Miller's monster or the Szilassi polyhedron
Szilassi polyhedron
The Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem...
.
Traditional polyhedra
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a polyhedron is traditionally a three-dimensional shape that is made up of a finite number of polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
al faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
which are parts of planes
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
; the faces meet in pairs along edges
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
which are straight-line segments, and the edges meet in points called vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. Cubes, prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
and pyramids
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
are examples of polyhedra. The polyhedron surrounds a bounded volume in three-dimensional space; sometimes this interior volume is considered to be part of the polyhedron, sometimes only the surface is considered, and occasionally only the skeleton of edges.
A polyhedron is said to be convex if its surface (comprising its faces, edges and vertices) does not intersect itself and the line segment joining any two points of the polyhedron is contained in the interior or surface.
Symmetrical polyhedra
Many of the most studied polyhedra are highly symmetricalSymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
.
Of course it is easy to distort such polyhedra so they are no longer symmetrical. But where a polyhedral name is given, such as icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, the most symmetrical geometry is almost always implied, unless otherwise stated.
Some of the most common names in particular are often used with "regular" in front or implied because for each there are different types which have little in common except for having the same number of faces. These are the triangular pyramid or tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
or hexahedron, octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, dodecahedron and icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
:
 |
 |
 |
 |
 |
Polyhedra of the highest symmetries have all of some kind of element - faces, edges and/or vertices, within a single symmetry orbit. There are various classes of such polyhedra:
- Isogonal or Vertex-transitiveVertex-transitiveIn geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
if all vertices are the same, in the sense that for any two vertices there exists a symmetrySymmetry groupThe symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the polyhedron mapping the first isometricallyIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
onto the second. - Isotoxal or Edge-transitive if all edges are the same, in the sense that for any two edges there exists a symmetry of the polyhedron mapping the first isometrically onto the second.
- Isohedral or Face-transitive if all faces are the same, in the sense that for any two faces there exists a symmetry of the polyhedron mapping the first isometrically onto the second.
- RegularRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
if it is vertex-transitive, edge-transitive and face-transitive (this implies that every face is the same regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
; it also implies that every vertex is regular). - Quasi-regularQuasiregular polyhedronIn geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
if it is vertex-transitive and edge-transitive (and hence has regular faces) but not face-transitive. A quasi-regular dual is face-transitive and edge-transitive (and hence every vertex is regular) but not vertex-transitive. - Semi-regularSemiregular polyhedronThe term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
if it is vertex-transitive but not edge-transitive, and every face is a regular polygon. (This is one of several definitions of the term, depending on author. Some definitions overlap with the quasi-regular class). A semi-regular dual is face-transitive but not vertex-transitive, and every vertex is regular. - UniformUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
if it is vertex-transitive and every face is a regular polygon, i.e. it is regular, quasi-regular or semi-regular. A uniform dual is face-transitive and has regular vertices, but is not necessarily vertex-transitive). - NobleNoble polyhedronA noble polyhedron is one which is isohedral and isogonal . They were first studied in any depth by Hess and Bruckner around the turn of the century , and later by Grünbaum.-Classes of noble polyhedra:...
if it is face-transitive and vertex-transitive (but not necessarily edge-transitive). The regular polyhedra are also noble; they are the only noble uniform polyhedra.
A polyhedron can belong to the same overall symmetry group as one of higher symmetry, but will have several groups of elements (for example faces) in different symmetry orbits.
Uniform polyhedra and their duals
Uniform polyhedra are vertex-transitiveVertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
and every face is a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
.
They may be regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
, quasi-regular
Quasiregular polyhedron
In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
, or semi-regular
Semiregular polyhedron
The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
, and may be convex or starry.
The uniform duals
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
are face-transitive and every vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a regular polygon.
Face-transitivity of a polyhedron corresponds to vertex-transitivity of the dual and conversely, and edge-transitivity of a polyhedron corresponds to edge-transitivity of the dual. The dual of a regular polyhedron is also regular. The dual of a non-regular uniform polyhedron (called a Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
if convex) has irregular faces.
Each uniform polyhedron shares the same symmetry as its dual, with the symmetries of faces and vertices simply swapped over. Because of this some authorities regard the duals as uniform too. But this idea is not held widely: a polyhedron and its symmetries are not the same thing.
The uniform polyhedra and their duals are traditionally classified according to their degree of symmetry, and whether they are convex or not.
| Convex uniform | Convex uniform dual | Star uniform | Star uniform dual | |
|---|---|---|---|---|
| Regular Regular polyhedron A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags... |
Platonic solid Platonic solid In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and... s |
Kepler-Poinsot polyhedra | ||
| Quasiregular Quasiregular polyhedron In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex... |
Archimedean solid Archimedean solid In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices... s |
Catalan solids | (no special name) | (no special name) |
| Semiregular Semiregular polyhedron The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron... |
(no special name) | (no special name) | ||
| Prisms Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
Dipyramids | Star Prisms Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
Star Dipyramids | |
| Antiprism Antiprism In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles... s |
Trapezohedra | Star Antiprism Antiprism In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles... s |
Star Trapezohedra | |
Noble polyhedra
A nobleNoble polyhedron
A noble polyhedron is one which is isohedral and isogonal . They were first studied in any depth by Hess and Bruckner around the turn of the century , and later by Grünbaum.-Classes of noble polyhedra:...
polyhedron is both isohedral (equal-faced) and isogonal (equal-cornered). Besides the regular polyhedra, there are many other examples.
The dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of a noble polyhedron is also noble.
Symmetry groups
The polyhedral symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s (using Schoenflies notation
Schoenflies notation
The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...
) are all point groups and include:
- T - chiral tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
; the rotation group for a regular tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
; order 12. - Td - full tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
; the symmetry group for a regular tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
; order 24. - Th - pyritohedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
; order 24. The symmetry of a pyritohedronPyritohedronIn geometry, a pyritohedron is an irregular dodecahedron with pyritohedral symmetry. Like the regular dodecahedron, it has twelve identical pentagonal faces, with three meeting in each of the 20 vertices. However, the pentagons are not regular, and the structure has no fivefold symmetry axes...
. - O - chiral octahedral symmetryOctahedral symmetry150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
;the rotation group of the cube and octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
; order 24. - Oh - full octahedral symmetryOctahedral symmetry150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
; the symmetry group of the cube and octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
; order 48. - I - chiral icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
; the rotation group of the icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and the dodecahedron; order 60. - Ih - full icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
; the symmetry group of the icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and the dodecahedron; order 120. - Cnv - n-fold pyramidal symmetryCyclic symmetriesThis article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
- Dnh - n-fold prismatic symmetry
- Dnv - n-fold antiprismatic symmetry.
Those with chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
symmetry do not have reflection symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
and hence have two enantiomorphous
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
forms which are reflections of each other. The snub Archimedean polyhedra have this property.
Equal regular faces
A few families of polyhedra, where every face is the same kind of polygon:- Deltahedra have equilateral triangles for faces.
- With regard to polyhedra whose faces are all squares: if coplanar faces are not allowed, even if they are disconnected, there is only the cube. Otherwise there is also the result of pasting six cubes to the sides of one, all seven of the same size; it has 30 square faces (counting disconnected faces in the same plane as separate). This can be extended in one, two, or three directions: we can consider the union of arbitrarily many copies of these structures, obtained by translations of (expressed in cube sizes) (2,0,0), (0,2,0), and/or (0,0,2), hence with each adjacent pair having one common cube. The result can be any connected set of cubes with positions (a,b,c), with integers a,b,c of which at most one is even.
- There is no special name for polyhedra whose faces are all equilateral pentagons or pentagrams. There are infinitely many of these, but only one is convex: the dodecahedron. The rest are assembled by (pasting) combinations of the regular polyhedra described earlier: the dodecahedron, the small stellated dodecahedron, the great stellated dodecahedron and the great icosahedron.
There exists no polyhedron whose faces are all identical and are regular polygons with six or more sides because the vertex of three regular hexagons defines a plane. (See infinite skew polyhedron
Infinite skew polyhedron
In geometry, an infinite skew polyhedron is an extension of the idea of a polyhedron, consisting of regular polygon faces with nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface....
for exceptions with zig-zagging vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s.)
Deltahedra
A deltahedron
Deltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
(plural deltahedra) is a polyhedron whose faces are all equilateral triangles. There are infinitely many deltahedra, but only eight of these are convex:
- 3 regular convex polyhedra (3 of the Platonic solids)
- TetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
- OctahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
- IcosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
- Tetrahedron
- 5 non-uniform convex polyhedra (5 of the Johnson solids)
- Triangular dipyramidTriangular dipyramidIn geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces....
- Pentagonal dipyramidPentagonal dipyramidIn geometry, the pentagonal bipyramid is third of the infinite set of face-transitive bipyramids.Each bipyramid is the dual of a uniform prism.If the faces are equilateral triangles, it is a deltahedron and a Johnson solid...
- Snub disphenoidSnub disphenoidIn geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...
- Triaugmented triangular prismTriaugmented triangular prismIn geometry, the triaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by attaching square pyramids to each of the three equatorial faces of the triangular prism...
- Gyroelongated square dipyramidGyroelongated square dipyramidIn geometry, the gyroelongated square bipyramid is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating an octahedron by inserting a square antiprism between its congruent halves...
.
- Triangular dipyramid
Johnson solids
Norman Johnson sought which convex non-uniform polyhedra had regular faces. In 1966, he published a list of 92 such solids, gave them names and numbers, and conjectured that there were no others. Victor ZalgallerVictor Zalgaller
Victor Abramovich Zalgaller is a mathematician in the fields of geometry and optimization. He is best known for his results on convex polyhedra, linear and dynamic programming, isoperimetry, and differential geometry....
proved in 1969 that the list of these Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s was complete.
Pyramids
Pyramids include some of the most time-honoured and famous of all polyhedra.Stellations and facettings
 |
 |
 |
 |
 |
 |
 |
Stellation of a polyhedron is the process of extending the faces (within their planes) so that they meet to form a new polyhedron.
It is the exact reciprocal to the process of facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
which is the process of removing parts of a polyhedron without creating any new vertices.
Zonohedra
A zonohedron is a convex polyhedron where every face is a polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with inversion symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
or, equivalently, symmetry under rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s through 180°.
Toroidal polyhedra
A toroidal polyhedron is a polyhedron with an Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of 0 or smaller, representing a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
surface.
Compounds
Polyhedral compounds are formed as compounds of two or more polyhedra.These compounds often share the same vertices as other polyhedra and are often formed by stellation. Some are listed in the list of Wenninger polyhedron models.
Orthogonal polyhedra
An orthogonal polyhedron is one all of whose faces meet at right angles, and all of whose edges are parallel to axes of a Cartesian coordinate system. Aside from a rectangular box, orthogonal polyhedra are nonconvex. They are the 3D analogs of 2D orthogonal polygons, also known as rectilinear polygonRectilinear polygon
A rectilinear polygon is a polygon all of whose edges meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons....
s. Orthogonal polyhedra are used in computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, where their constrained structure has enabled advances on problems unsolved for arbitrary polyhedra, for example, unfolding the surface of a polyhedron to a polygonal net.
Generalisations of polyhedra
The name 'polyhedron' has come to be used for a variety of objects having similar structural properties to traditional polyhedra.Apeirohedra
A classical polyhedral surface comprises finite, bounded plane regions, joined in pairs along edges. If such a surface extends indefinitely it is called an apeirohedronApeirohedron
An apeirohedron is a polyhedron having infinitely many faces. Like an ordinary polyhedron it forms a surface with no border. But where an ordinary polyhedral surface has no border because it folds round to close back on itself, an apeirohedron has no border because its surface is unbounded.Two main...
. Examples include:
- Tilings or tessellationTessellationA tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s of the plane. - Sponge-like structures called infinite skew polyhedraInfinite skew polyhedronIn geometry, an infinite skew polyhedron is an extension of the idea of a polyhedron, consisting of regular polygon faces with nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface....
.
See also: Apeirogon
Apeirogon
An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...
- infinite regular polygon: {∞}
Complex polyhedra
A complex polyhedronComplex polytope
A complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one....
is one which is constructed in complex Hilbert
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
3-space. This space has six dimensions: three real ones corresponding to ordinary space, with each accompanied by an imaginary dimension. See for example Coxeter (1974).
Spherical polyhedra
The surface of a sphere may be divided by line segments into bounded regions, to form a spherical polyhedron. Much of the theory of symmetrical polyhedra is most conveniently derived in this way.Spherical polyhedra have a long and respectable history:
- The first known man-made polyhedra are spherical polyhedra carved in stone.
- Poinsot used spherical polyhedra to discover the four regular star polyhedra.
- Coxeter used them to enumerate all but one of the uniform polyhedra.
Some polyhedra, such as hosohedra and dihedra
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
, exist only as spherical polyhedra and have no flat-faced analogue.
Curved spacefilling polyhedra
Two important types are:- Bubbles in froths and foams, such as Weaire-Phelan bubbles.
- Spacefilling forms used in architecture. See for example Pearce (1978).
General polyhedra
More recently mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
has defined a polyhedron as a set in real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
affine
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
(or Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
) space of any dimensional n that has flat sides. It may alternatively be defined as the union of a finite number of convex polyhedra, where a convex polyhedron is any set that is the intersection of a finite number of half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
s. It may be bounded or unbounded. In this meaning, a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
is a bounded polyhedron.
Analytically, such a convex polyhedron is expressed as the solution set for a system of linear inequalities. Defining polyhedra (and more generally polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s) in this way provides a geometric perspective for problems in Linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
.
Many traditional polyhedral forms are general polyhedra. Other examples include:
- A quadrant in the plane. For instance, the region of the cartesian plane consisting of all points above the horizontal axis and to the right of the vertical axis: { ( x, y ) : x ≥ 0, y ≥ 0 }. Its sides are the two positive axes.
- An octant in Euclidean 3-space, { ( x, y, z ) : x ≥ 0, y ≥ 0, z ≥ 0 }.
- A prism of infinite extent. For instance a doubly infinite square prism in 3-space, consisting of a square in the xy-plane swept along the z-axis: { ( x, y, z ) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 }.
- Each cellCell (geometry)In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
in a Voronoi tessellationVoronoi diagramIn mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
is a convex polyhedron. In the Voronoi tessellation of a set S, the cell A corresponding to a point c∈S is bounded (hence a traditional polyhedron) when c lies in the interiorInterior (topology)In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of S, and otherwise (when c lies on the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the convex hull of S) A is unbounded.
Hollow faced or skeletal polyhedra
It is not necessary to fill in the face of a figure before we can call it a polyhedron. For example Leonardo da VinciLeonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
devised frame models of the regular solids, which he drew for Pacioli's book Divina Proportione. In modern times, Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
(1994) made a special study of this class of polyhedra, in which he developed an early idea of abstract polyhedra. He defined a face as a cyclically ordered set of vertices, and allowed faces to be skew
Skew polygon
In geometry, a skew polygon is a polygon whose vertices do not lie in a plane. Skew polygons must have at least 4 vertices.A regular skew polygon is a skew polygon with equal edge lengths and which is vertex-transitive....
as well as planar.
Non-geometric polyhedra
Various mathematical constructs have been found to have properties also present in traditional polyhedra.Topological polyhedra
A topological polytope is a topological space given along with a specific decomposition into shapes that are topologically equivalent to convex polytopeConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s and that are attached to each other in a regular way.
Such a figure is called simplicial if each of its regions is a simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, i.e. in an n-dimensional space each region has n+1 vertices. The dual of a simplicial polytope is called simple. Similarly, a widely studied class of polytopes (polyhedra) is that of cubical polyhedra, when the basic building block is an n-dimensional cube.
Abstract polyhedra
An abstract polyhedron is a partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(poset) of elements whose partial ordering obeys certain rules. Theories differ in detail, but essentially the elements of the set correspond to the body, faces, edges and vertices of the polyhedron. The empty set corresponds to the null polytope, or nullitope, which has a dimensionality of −1. These posets belong to the larger family of abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s in any number of dimensions.
Polyhedra as graphs
Any polyhedron gives rise to a graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, or skeleton, with corresponding vertices and edges. Thus graph terminology
Glossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
and properties can be applied to polyhedra. For example:
- Due to Steinitz theorem convex polyhedra are in one-to-one correspondence with 3-connected planar graphs.
- The tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
gives rise to a complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
(K4). It is the only polyhedron to do so. - The octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
gives rise to a strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
, because adjacent vertices always have two common neighbors, and non-adjacent vertices have four. - The Archimedean solidArchimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s give rise to regular graphRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s: 7 of the Archimedean solids are of degreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
3, 4 of degree 4, and the remaining 2 are chiral pairs of degree 5.
Prehistory
Stones carved in shapes showing the symmetries of various polyhedra have been found in ScotlandScotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
and may be as much as 4,000 years old. These stones show not only the form of various symmetrical polyehdra, but also the relations of duality amongst some of them (that is, that the centres of the faces of the cube gives the vertices of an octahedron, and so on). Examples of these stones are on display in the John Evans room of the Ashmolean Museum
Ashmolean Museum
The Ashmolean Museum on Beaumont Street, Oxford, England, is the world's first university museum...
at Oxford University. It is impossible to know why these objects were made, or how the sculptor gained the inspiration for them.
Other polyhedra have of course made their mark in architecture
Architecture
Architecture is both the process and product of planning, designing and construction. Architectural works, in the material form of buildings, are often perceived as cultural and political symbols and as works of art...
—cubes and cuboids being obvious examples, with the earliest four-sided pyramids of ancient Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
also dating from the Stone Age.
The Etruscans
Etruscan civilization
Etruscan civilization is the modern English name given to a civilization of ancient Italy in the area corresponding roughly to Tuscany. The ancient Romans called its creators the Tusci or Etrusci...
preceded the Greeks in their awareness of at least some of the regular polyhedra, as evidenced by the discovery near Padua
Padua
Padua is a city and comune in the Veneto, northern Italy. It is the capital of the province of Padua and the economic and communications hub of the area. Padua's population is 212,500 . The city is sometimes included, with Venice and Treviso, in the Padua-Treviso-Venice Metropolitan Area, having...
(in Northern Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
) in the late 19th century of a dodecahedron made of soapstone
Soapstone
Soapstone is a metamorphic rock, a talc-schist. It is largely composed of the mineral talc and is thus rich in magnesium. It is produced by dynamothermal metamorphism and metasomatism, which occurs in the areas where tectonic plates are subducted, changing rocks by heat and pressure, with influx...
, and dating back more than 2,500 years (Lindemann, 1987). Pyritohedric crystals are found in northern Italy.
Greeks
The earliest known written records of these shapes come from Classical GreekAncient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
authors, who also gave the first known mathematical description of them. The earlier Greeks were interested primarily in the convex regular polyhedra, which came to be known as the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s. Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
knew at least three of them, and Theaetetus
Theaetetus (mathematician)
Theaetetus, Theaitētos, of Athens, possibly son of Euphronius, of the Athenian deme Sunium, was a classical Greek mathematician...
(circa 417 B. C.) described all five. Eventually, Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
described their construction in his Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
. Later, Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
expanded his study to the convex uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
which now bear his name. His original work is lost and his solids come down to us through Pappus
Pappus of Alexandria
Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
.
Chinese
By 236 AD, in China Liu Hui was describing the dissection of the cube into its characteristic tetrahedron (orthoscheme) and related solids, using assemblages of these solids as the basis for calculating volumes of earth to be moved during engineering excavations.Islamic
After the end of the Classical era, scholars in the Islamic civilisation continued to take the Greek knowledge forward (see Mathematics in medieval Islam).The 9th century scholar Thabit ibn Qurra
Thabit ibn Qurra
' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
gave formulae for calculating the volumes of polyhedra such as truncated pyramids.
Then in the 10th century Abu'l Wafa described the convex regular and quasiregular spherical polyhedra.
Renaissance
As with other areas of Greek thought maintained and enhanced by Islamic scholars, Western interest in polyhedra revived during the Italian RenaissanceRenaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
. Artists constructed skeletal polyhedra, depicting them from life as a part of their investigations into perspective
Perspective
- Literally, in visual topics :* Perspective , the way in which objects appear to the eye.* Perspective , representing the effects of visual perspective in graphic arts- Metaphorically, in relation to cognitive topics :...
. Several appear in marquetry panels of the period. Piero della Francesca gave the first written description of direct geometrical construction of such perspective views of polyhedra. Leonardo da Vinci made skeletal models of several polyhedra and drew illustrations of them for a book by Pacioli. A painting by an anonymous artist of Pacioli and a pupli depicts a glass rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
half-filled with water.
As the Renaissance spread beyond Italy, later artists such as Wenzel Jamnitzer, Dürer and others also depicted polyhedra of various kinds, many of them novel, in imaginative etchings.
Star polyhedra
For almost 2,000 years, the concept of a polyhedron as a convex solid had remained as developed by the ancient Greek mathematicians.During the Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
star forms were discovered. A marble tarsia in the floor of St. Mark's Basilica, Venice, depicts a stellated dodecahedron. Artists such as Wenzel Jamnitzer delighted in depicting novel star-like forms of increasing complexity.
Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
realised that star polygons, typically pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
s, could be used to build star polyhedra. Some of these star polyhedra may have been discovered before Kepler's time, but he was the first to recognise that they could be considered "regular" if one removed the restriction that regular polytopes be convex. Later, Louis Poinsot
Louis Poinsot
Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
realised that star vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s (circuits around each corner) can also be used, and discovered the remaining two regular star polyhedra. Cauchy proved Poinsot's list complete, and Cayley gave them their accepted English names: (Kepler's) the small stellated dodecahedron and great stellated dodecahedron, and (Poinsot's) the great icosahedron and great dodecahedron. Collectively they are called the Kepler-Poinsot polyhedra.
The Kepler-Poinsot polyhedra may be constructed from the Platonic solids by a process called stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
. Most stellations are not regular. The study of stellations of the Platonic solids was given a big push by H. S. M. Coxeter and others in 1938, with the now famous paper The 59 icosahedra. This work has recently been re-published (Coxeter, 1999).
The reciprocal process to stellation is called facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
(or faceting). Every stellation of one polytope is dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
, or reciprocal, to some facetting of the dual polytope. The regular star polyhedra can also be obtained by facetting the Platonic solids. listed the simpler facettings of the dodecahedron, and reciprocated them to discover a stellation of the icosahedron that was missing from the famous "59". More have been discovered since, and the story is not yet ended.
See also:
- Regular polyhedron: History
- Regular polytope: History of discovery.
Polyhedra in nature
For natural occurrences of regular polyhedra, see Regular polyhedron: Regular polyhedra in nature.Irregular polyhedra appear in nature as crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s.
General theory
- Polyhedra Pages
- uniform solution for uniform polyhedra by Dr. Zvi Har'El
- Symmetry, Crystals and Polyhedra
- Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons
Lists and databases of polyhedra
- The Uniform Polyhedra
- Virtual Reality Polyhedra - The Encyclopedia of Polyhedra
- Interactive 3D polyhedra in Java
- Electronic Geometry Models - Contains a peer reviewed selection of polyhedra with unusual properties.
- Origami Polyhedra - Models made with Modular Origami
- Polyhedra Collection - Various virtual and physical polyhedra models.
- Polyhedra plaited with paper strips - Polyhedra models constructed without use of glue.
- Rotatable polyhedron models (uses Javascript)
- Rotatable self-intersecting polyhedra (uses Java)
- Polyhedron Models - Virtual polyhedra
- Java Applets for Visualizing Polyhedra - Systematically explicit formulae given!
Software
- A Plethora of Polyhedra – An interactive and free collection of polyhedra in Java. Features includes nets, planar sections, duals, truncations and stellations of more than 300 polyhedra.
- Stella: Polyhedron Navigator - Software for exploring polyhedra and printing nets for their physical construction. Includes uniform polyhedra, stellations, compounds, Johnson solids, etc.
- World of Polyhedra - Comprehensive polyhedra in Flash applet, showing vertices and edges (but not shaded faces)
- Hyperspace Star Polytope Slicer - Explorer java applet, includes a variety of 3d viewer options.
- HEDRON Polyhedron modelling software
- Uniform Polyhedra Java Applets with sources
Resources for making models, and models for sale
- Making Polyhedra
- Paper Models of Polyhedra Free nets of polyhedra
- Paper Models of Uniform (and other) Polyhedra
- Kits and instructions for making models of polyhedra out of bamboo
- Polyhedra software, die-cast models, & posters
- Simple instructions for building over 30 paper polyhedra
- Kits to print out, cut, and fold into various polyhedra
- openSCAD. Free cross-platform software for programmers. Polyhedra are just one of the things you can model. The openSCAD User Manual is also available.
Miscellaneous
- PictureSpice - A site that lets you make polyhedra with your own uploaded pictures.
- Lattice Polyhedra