.gif)
Golden triangle (mathematics)
Encyclopedia
A golden triangle, also known as the sublime triangle,
is an isosceles triangle
in which the smaller side is in golden ratio
with its adjacent side:
Golden triangles are found in the nets of several stellations of dodecahedrons and icosahedron
s.
Also, it is the shape of the triangles found in the points of pentagram
s.
The vertex angle is equal to
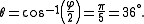
Since the angles of a triangle sum to 180°, base angles are therefore 72° each.
The golden triangle can also be found in a decagon
, or a ten-sided polygon, by connecting any two adjacent vertices to the center. This will form a golden triangle. This is because:
180(10-2)/2=144 degrees is the interior angle and bisecting it through the vertex to the center, 144/2=72.
The golden triangle is also uniquely identified as the only triangle to have its three angles in 2:2:1 proportion.
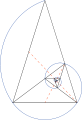The golden triangle is used to form a logarithmic spiral
. By bisecting the base angles, a new point is created that in turn, makes another golden triangle.
The bisection process can be continued infinitely, creating an infinite number of golden triangles. A logarithmic spiral
can be drawn through the vertices. This spiral is also known as an equiangular spiral, a term coined by Rene Descartes
. "If a straight line is drawn from the pole to any point on the curve, it cuts the curve at precisely the same angle," hence equiangular.
.svg.png)
Closely related to the golden triangle is the golden gnomon
, which is the obtuse isosceles triangle in which the ratio of the length of the equal (shorter) sides to the length of the third side is the reciprocal of the golden ratio. The golden gnomon is also uniquely identified as a triangle having its three angles in 1:1:3 proportion. The acute angle is 36 degrees, which is the same as the apex of the golden triangle.
The distance of AD and BD are both equal to φ, as seen in the figure. "The golden triangle has a ratio of base length to side length equal to the golden section φ, whereas the golden gnomon has the ratio of side length to base length equal to the golden section φ."
A golden triangle can be bisected into a golden triangle and a golden gnomon. The same is true for a golden gnomon. A golden gnomon and a golden triangle with their equal sides matching each other in length, are also referred to as the obtuse and acute Robinson triangles.
These isosceles triangles can be used to produce Penrose tiling
s. Penrose tiles are made from kites and darts. A kite is made from the golden triangle, and a dart is made from two gnomons.
. He states that her figure is organized by the golden triangle.
is an isosceles triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
in which the smaller side is in golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
with its adjacent side:
Golden triangles are found in the nets of several stellations of dodecahedrons and icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
s.
Also, it is the shape of the triangles found in the points of pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
s.
The vertex angle is equal to
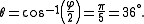
Since the angles of a triangle sum to 180°, base angles are therefore 72° each.
The golden triangle can also be found in a decagon
Decagon
In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
, or a ten-sided polygon, by connecting any two adjacent vertices to the center. This will form a golden triangle. This is because:
180(10-2)/2=144 degrees is the interior angle and bisecting it through the vertex to the center, 144/2=72.
The golden triangle is also uniquely identified as the only triangle to have its three angles in 2:2:1 proportion.
Logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
. By bisecting the base angles, a new point is created that in turn, makes another golden triangle.
The bisection process can be continued infinitely, creating an infinite number of golden triangles. A logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
can be drawn through the vertices. This spiral is also known as an equiangular spiral, a term coined by Rene Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
. "If a straight line is drawn from the pole to any point on the curve, it cuts the curve at precisely the same angle," hence equiangular.
Golden gnomon
Gnomon (figure)
In geometry, a gnomon is a plane figure formed by removing a similar parallelogram from a corner of a larger parallelogram. More generically, the term gnomon denotes the form that is to be added to a figure to produce a larger figure of the same shape....
, which is the obtuse isosceles triangle in which the ratio of the length of the equal (shorter) sides to the length of the third side is the reciprocal of the golden ratio. The golden gnomon is also uniquely identified as a triangle having its three angles in 1:1:3 proportion. The acute angle is 36 degrees, which is the same as the apex of the golden triangle.
The distance of AD and BD are both equal to φ, as seen in the figure. "The golden triangle has a ratio of base length to side length equal to the golden section φ, whereas the golden gnomon has the ratio of side length to base length equal to the golden section φ."
A golden triangle can be bisected into a golden triangle and a golden gnomon. The same is true for a golden gnomon. A golden gnomon and a golden triangle with their equal sides matching each other in length, are also referred to as the obtuse and acute Robinson triangles.
These isosceles triangles can be used to produce Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s. Penrose tiles are made from kites and darts. A kite is made from the golden triangle, and a dart is made from two gnomons.
The golden triangle in art
In his book, Math and the Mona Lisa, Atalay says that the golden triangle can be found in the Mona LisaMona Lisa
Mona Lisa is a portrait by the Italian artist Leonardo da Vinci. It is a painting in oil on a poplar panel, completed circa 1503–1519...
. He states that her figure is organized by the golden triangle.
See also
- Kepler triangle
- Golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
- Golden rectangle
- Pentagram
- Golden rhombus
External links
- Golden triangle article at Wolfram MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Robinson triangles at Tilings Encyclopedia