
Differentiable manifold
Encyclopedia
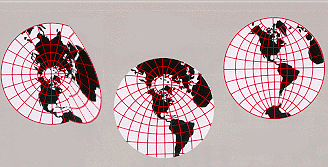
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
that is locally similar enough to a linear space to allow one to do calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. Any manifold can be described by a collection of charts
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. Note that a differentiable manifold as it stands does not have any metric structure or any notion of orthogonality. The addition of metric (or pseudo-metric) structure corresponds to the linear space mentioned above actually being Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(or pseudo-Euclidean space).
In formal terms, a differentiable manifold is a topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
with a globally defined differential structure
Differential structure
In mathematics, an n-dimensional differential structure on a set M makes M into an n-dimensional differential manifold, which is a topological manifold with some additional structure that allows us to do differential calculus on the manifold...
. Any topological manifold can be given a differential structure locally by using the homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s in its atlas and the standard differential structure on a linear space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, their composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
on chart intersections in the atlas must be differentiable functions on the corresponding linear space. In other words, where the domains of charts overlap, the coordinates defined by each chart are required to be differentiable with respect to the coordinates defined by every chart in the atlas. The maps that relate the coordinates defined by the various charts to one another are called transition maps.
Differentiability means different things in different contexts including: continuously differentiable
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, k times differentiable, and holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
. Furthermore, the ability to induce such a differential structure on an abstract space allows one to extend the definition of differentiability to spaces without global coordinate systems. A differential structure allows one to define the globally differentiable tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
, differentiable functions, and differentiable tensor
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
and vector
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
fields. Differentiable manifolds are very important in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. Special kinds of differentiable manifolds form the basis for physical theories such as classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, and Yang-Mills theory.
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
It is possible to develop a calculus for differentiable manifolds. This leads to such mathematical machinery as the exterior calculus.
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
The study of calculus on differentiable manifolds is known as differential geometry.
Differential geometry and topology
Differential geometry is a mathematical discipline that uses the techniques of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis...
History
The emergence of differential geometry as a distinct discipline is generally credited to Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
. Riemann first described manifolds in his famous habilitation lecture before the faculty at Göttingen. He motivated the idea of a manifold by an intuitive process of varying a given object in a new direction, and presciently described the role of coordinate systems and charts in subsequent formal developments:
- Having constructed the notion of a manifoldness of n dimensions, and found that its true character consists in the property that the determination of position in it may be reduced to n determinations of magnitude, ... - B. Riemann
The works of physicists such as James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, and mathematicians Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
and Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
led to the development of tensor analysis and the notion of covariance
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
, which identifies an intrinsic geometric property as one that is invariant with respect to coordinate transformations. These ideas found a key application in Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and its underlying equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
. A modern definition of a 2-dimensional manifold was given by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in his 1913 book on Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s. The widely accepted general definition of a manifold in terms of an atlas is due to Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
.
Definition
A presentation of a topological manifold is a second countable HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is locally homeomorphic to a linear space, by a collection (called an atlas) of homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s called charts. The composition of one chart with the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of another chart is a function called a transition map, and defines a homeomorphism of an open subset of the linear space onto another open subset of the linear space. This formalizes the notion of "patching together pieces of a space to make a manifold" – the manifold produced also contains the data of how it has been patched together. However, different atlases (patchings) may produce "the same" manifold, and, on the converse, a manifold does not come with a preferred atlas. And, thus, one defines a topological manifold to be a space as above with an equivalence class of atlases, where one defines equivalence of atlases below.
There are a number of different types of differentiable manifolds, depending on the precise differentiability requirements on the transition functions. Some common examples include the following.
- A differentiable manifold is a topological manifold equipped with an equivalence class of atlases whose transition maps are all differentiable. In broader terms, a Ck-manifold is a topological manifold with an atlas whose transition maps are all k-times continuously differentiable.
- A smooth manifold or C∞-manifold is a differentiable manifold for which all the transition maps are smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. That is, derivatives of all orders exist; so it is a Ck-manifold for all k.
- An analytic manifold, or Cω-manifold is a smooth manifold with the additional condition that each transition map is analyticAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
: the Taylor expansion is absolutely convergent and equals the function on some open ball.
- A complex manifold is a topological space modeled on a Euclidean space over the complex field and for which all the transition maps are holomorphic.
While there is a meaningful notion of a Ck atlas, there is no distinct notion of a Ck manifold other than C0 (continuous maps: a topological manifold) and C∞ (smooth maps: a smooth manifold), because every Ck-structure with
 there is a unique Ck-equivalent C∞-structure (every Ck-structure is uniquely smoothable) – a result of Whitney
there is a unique Ck-equivalent C∞-structure (every Ck-structure is uniquely smoothable) – a result of WhitneyHassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
(and further, two Ck atlases that are equivalent to a single C∞ atlas are equivalent as Ck atlases, so two distinct Ck atlases do not collide); see Differential structure: Existence and uniqueness theorems for details. Thus one uses the terms "differentiable manifold" and "smooth manifold" interchangeably. This is in stark contrast to Ck maps, where there are meaningful differences for different k. For example, the Nash embedding theorem
Nash embedding theorem
The Nash embedding theorems , named after John Forbes Nash, state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path...
states that any manifold can be Ck isometrically embedded in Euclidean space RN – for any 1 ≤ k ≤ ∞ there is a sufficiently large N, but N depends on k.
On the other hand, complex manifolds are significantly more restrictive. As an example, Chow's theorem states that any projective complex manifold is in fact a projective variety – it has an algebraic structure.
Atlases
An atlasAtlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
on a topological space X is a collection of pairs {(Uα,φα)} called charts, where the Uα are open sets that cover X, and for each index α

is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of Uα onto an open subset of n-dimensional real space. The transition maps of the atlas are the functions

Every topological manifold has an atlas. A Ck-atlas is an atlas whose transition maps are Ck. A topological manifold has a C0-atlas and in general a Ck-manifold has a Ck-atlas. A continuous atlas is a C0 atlas, a smooth atlas is a C∞ atlas and an analytic atlas is a Cω atlas. If the atlas is at least C1, it is also called a differential structure or differentiable structure. A holomorphic atlas is an atlas whose underlying Euclidean space is defined on the complex field and whose transition maps are biholomorphic.
Compatible atlases
Different atlases can give rise to, in essence, the same manifold. The circle can be mapped by two coordinate charts, but if the domains of these charts are changed slightly a different atlas for the same manifold is obtained. These different atlases can be combined into a bigger atlas. It can happen that the transition maps of such a combined atlas are not as smooth as those of the constituent atlases. If Ck atlases can be combined to form a Ck atlas, then they are called compatible. Compatibility of atlases is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
; by combining all the atlases in an equivalence class, a maximal atlas can be constructed. Each Ck atlas belongs to a unique maximal Ck atlas.
Pseudogroups
The notion of a pseudogroupPseudogroup
In mathematics, a pseudogroup is an extension of the group concept, but one that grew out of the geometric approach of Sophus Lie, rather than out of abstract algebra...
provides a flexible generalization of atlases in order to allow a variety of different structures to be defined on manifolds in a uniform way. A pseudogroup consists of a topological space S and a collection
 consisting of homeomorphisms from open subsets of S to other open subsets of S such that
consisting of homeomorphisms from open subsets of S to other open subsets of S such that
- If
 , and
, and  is an open subset of the domain of
is an open subset of the domain of  , then the restriction
, then the restriction  is also in
is also in  .
. - If
 is a homeomorphism from a union of open subsets of
is a homeomorphism from a union of open subsets of  ,
,  , to an open subset of
, to an open subset of  , then
, then  provided
provided  for every
for every  .
. - For every open
 , the identity transformation of
, the identity transformation of  is in
is in  .
. - If
 , then
, then  .
. - The composition of two elements of
 is in
is in  .
.
These last three conditions are analogous to the definition of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Note that
 need not be a group, however, since the functions are not globally defined on
need not be a group, however, since the functions are not globally defined on  . For example, the collection of all local Ck diffeomorphisms on Rn form a pseudogroup. All biholomorphisms between open sets in Cn form a pseudogroup. More examples include: orientation preserving maps of Rn, symplectomorphism
. For example, the collection of all local Ck diffeomorphisms on Rn form a pseudogroup. All biholomorphisms between open sets in Cn form a pseudogroup. More examples include: orientation preserving maps of Rn, symplectomorphismSymplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s, Moebius transformations, affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s, and so on. Thus a wide variety of function classes determine pseudogroups.
An atlas (Ui, φi) of homeomorphisms φi from Ui ⊂ M to open subsets of a topological space S is said to be compatible with a pseudogroup
 provided that the transition functions φj o φi−1 : φi(Ui ∩ Uj) → φj(Ui ∩ Uj) are all in
provided that the transition functions φj o φi−1 : φi(Ui ∩ Uj) → φj(Ui ∩ Uj) are all in  .
.A differentiable manifold is then an atlas compatible with the pseudogroup of Ck functions on Rn. A complex manifold is an atlas compatible with the biholomorphic functions on open sets in Cn. And so forth. Thus pseudogroups provide a single framework in which to describe many structures on manifolds of importance to differential geometry and topology.
Structure sheaf
Sometimes it can be useful to use an alternative approach to endow a manifold with a Ck-structure. Here k = 1, 2, ..., ∞, or ω for real analytic manifolds. Instead of considering coordinate charts, it is possible to start with functions defined on the manifold itself. The structure sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of M, denoted Ck, is a sort of functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
that defines, for each open set U ⊂ M, an algebra Ck(U) of continuous functions U → R. A structure sheaf Ck is said to give M the structure of a Ck manifold of dimension n provided that, for any p ∈ M, there exists a neighborhood U of p and n functions x1,...,xn ∈ Ck(U) such that the map f = (x1, ..., xn) : U → Rn is a homeomorphism onto an open set in Rn, and such that Ck|U is the pullback
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
of the sheaf of k-times continuously differentiable functions on Rn.
In particular, this latter condition means that any function h in Ck(V), for V, can be written uniquely as h(x) = H(x1(x),...,xn(x)), where H is a k-times differentiable function on f(V) (an open set in Rn). Thus, the sheaf-theoretic viewpoint is that the functions on a differentiable manifold can be expressed in local coordinates as differentiable functions on Rn, and a fortiori
A fortiori argument
The Latin phrase ' denotes "argument 'from [the] stronger [reason]'." For example, if it has been established that a person is deceased, then one can, with equal or greater certainty, argue that the person is not breathing.-Usage:...
this is sufficient to characterize the differential structure on the manifold.
Sheaves of local rings
A similar, but more technical, approach to defining differentiable manifolds can be formulated using the notion of a ringed spaceRinged space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
. This approach is strongly influenced by the theory of schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, but uses local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s of the germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of differentiable functions. It is especially popular in the context of complex manifolds.
We begin by describing the basic structure sheaf on Rn. If U is an open set in Rn, let
- O(U) = Ck(U,R)
consist of all real-valued k-times continuously differentiable functions on U. As U varies, this determines a sheaf of rings on Rn. The stalk Op for p ∈ Rn consists of germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of functions near p, and is an algebra over R. In particular, this is a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
whose unique maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
consists of those functions that vanish at p. The pair (Rn, O) is an example of a locally ringed space: it is a topological space equipped with a sheaf whose stalks are each local rings.
A differentiable manifold (of class Ck) consists of a pair (M, OM) where M is a topological space, and OM is a sheaf of local R-algebras defined on M, such that the locally ringed space (M,OM) is locally isomorphic to (Rn, O). In this way, differentiable manifolds can be thought of as schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
modelled on Rn. This means that, for each point p ∈ M, there is a neighborhood U of p, and a pair of functions (f,f#) where
- f : U → f(U) ⊂ Rn is a homeomorphism onto an open set in Rn.
- f# : O|f(U) → f* (OM|U) is an isomorphism of sheaves.
- The localization of f# is an isomorphism of local rings
-
- f#p : Of(p) → OM, p.
There are a number of important motivations for studying differentiable manifolds within this abstract framework. First, there is no a priori reason that the model space needs to be Rn. For example (in particular in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
), one could take this to be the space of complex numbers Cn equipped with the sheaf of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s (thus arriving at the spaces of complex analytic geometry
Complex analytic geometry
In mathematics, complex analytic geometry sometimesdenotes the application of complex numbers to plane geometry.Rather than represent a point in the plane as a pair of Cartesian coordinates, it can be represented as a single complex number, which can be written at will in either rectangular or...
), or the sheaf of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s (thus arriving at the spaces of interest in complex algebraic geometry). In broad terms, this concept can be adapted for any suitable notion of a scheme (see topos theory). Second, coordinates are no longer explicitly necessary to the construction. The analog of a coordinate system is the pair (f, f#), but these merely quantify the idea of local isomorphism rather than being central to the discussion (as in the case of charts and atlases). Third, the sheaf OM is not manifestly a sheaf of functions at all. Rather, it emerges as a sheaf of functions as a consequence of the construction (via the quotients of local rings by their maximal ideals). Hence it is a more primitive definition of the structure (see synthetic differential geometry
Synthetic differential geometry
In mathematics, synthetic differential geometry is a reformulation of differential geometry in the language of topos theory, in the context of an intuitionistic logic characterized by a rejection of the law of excluded middle. There are several insights that allow for such a reformulation...
).
A final advantage of this approach is that it allows for natural direct descriptions of many of the fundamental objects of study to differential geometry and topology.
- The cotangent spaceCotangent spaceIn differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
at a point is Ip/Ip2, where Ip is the maximal ideal of the stalk OM,p. - In general, the entire cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
can be obtained by a related technique (see cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
for details). - Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
(and jetsJet (mathematics)In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
) can be approached in a coordinate-independent manner using the Ip-adic filtrationCompletion (ring theory)In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
on OM,p. - The tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
(or more precisely its sheaf of sections) can be identified with the sheaf of morphisms of OM into the ring of dual numbers.
Differentiable functions
A real valued function f on an m-dimensional differentiable manifold M is called differentiable at a point p ∈ M if it is differentiable in any coordinate chart defined around p. In more precise terms, if (U, φ) is a chart where U is an open set in M containing p and φ : U → Rn is the map defining the chart, then f is differentiable if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

is differentiable at φ(p). The definition of differentiability depends on the choice of chart at p; in general there will be many available charts. However, it follows from the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
applied to the transition functions between one chart and another that if f is differentiable in any particular chart at p, then it is differentiable in all charts at p. Analogous considerations apply to defining Ck functions, smooth functions, and analytic functions.
Differentiation of functions
There are various ways to define the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function on a differentiable manifold, the most fundamental of which is the directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
. The definition of the directional derivative is complicated by the fact that a manifold will lack a suitable affine
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
structure with which to define vectors. The directional derivative therefore looks at curves in the manifold instead of vectors.
Directional differentiation
Given a real valued function f on an m dimensional differentiable manifold M, the directional derivative of f at a point p in M is defined as follows. Suppose that γ(t) is a curve in M with γ(0) = p, which is differentiable in the sense that its composition with any chart is a differentiable curve in Rm. Then the directional derivative of f at p along γ is
If γ1 and γ2 are two curves such that γ1(0) = γ2(0) = p, and in any coordinate chart φ,

then, by the chain rule, f has the same directional derivative at p along γ1 as along γ2. This means that the directional derivative depends only on the tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
of the curve at p. Thus the more abstract definition of directional differentiation adapted to the case of differentiable manifolds ultimately captures the intuitive features of directional differentiation in an affine space.
Tangent vectors and the differential
A tangent vector at p ∈ M is an equivalence class of differentiable curves γ with γ(0) = p, modulo the equivalence relation of first-order contactContact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
between the curves. Therefore,

in any (and hence all) coordinate charts φ. Therefore, the equivalence classes are curves through p with a prescribed velocity vector at p. The collection of all tangent vectors at p forms a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
: the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to M at p, denoted TpM.
If X is a tangent vector at p and f a differentiable function defined near p, then differentiating f along any curve in the equivalence class defining X gives a well-defined directional derivative along X:

Once again, the chain rule establishes that this is independent of the freedom in selecting γ from the equivalence class, since any curve with the same first order contact will yield the same directional derivative.
If the function f is fixed, then the mapping

is a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the tangent space. This linear functional is often denoted by df(p) and is called the differential of f at p:

Partitions of unity
One of the topological features of the sheaf of differentiable functions on a differentiable manifold is that it admits partitions of unity. This distinguishes the differential structure on a manifold from stronger structures (such as analytic and holomorphic structures) that in general fail to have partitions of unity.Suppose that M is a manifold of class Ck, where 0 ≤ k ≤ ∞. Let {Uα} be an open covering of M. Then a partition of unity subordinate to the cover {Uα} is a collection of real-valued Ck functions φi on M satisfying the following conditions:
- The supportsSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of the φi are compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and locally finiteLocally finite collectionIn the mathematical field of topology, local finiteness is a property of collections of subsets of a topological space. It is fundamental in the study of paracompactness and topological dimension....
; - The support of φi is completely contained in Uα for some α;
- The φi sum to one at each point of M:
(Note that this last condition is actually a finite sum at each point because of the local finiteness of the supports of the φi.)
Every open covering of a Ck manifold M has a Ck partition of unity. This allows for certain constructions from the topology of Ck functions on Rn to be carried over to the category of differentiable manifolds. In particular, it is possible to discuss integration by choosing a partition of unity subordinate to a particular coordinate atlas, and carrying out the integration in each chart of Rn. Partitions of unity therefore allow for certain other kinds of function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s to be considered: for instance Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, Sobolev spaces, and other kinds of spaces that require integration.
Differentiability of mappings between manifolds
Suppose M and N are two differentiable manifolds with dimensions m and n, respectively, and f is a function from M to N. Since differentiable manifolds are topological spaces we know what it means for f to be continuous. But what does "f is Ck(M, N)" mean for k≥1? We know what that means when f is a function between Euclidean spaces, so if we compose f with a chart of M and a chart of N such that we get a map that goes from Euclidean space to M to N to Euclidean space we know what it means for that map to be Ck(Rm, Rn). We define "f is Ck(M, N)" to mean that all such compositions of f with charts are Ck(Rm, Rn). Once again the chain rule guarantees that the idea of differentiability does not depend on which charts of the atlases on M and N are selected. However, defining the derivative itself is more subtle. If M or N is itself already a Euclidean space, then we don't need a chart to map it to one.Algebra of scalars
For a Ck manifold M, the set of real-valued Ck functions on the manifold forms an algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
under pointwise addition and multiplication, called the algebra of scalar fields or simply the algebra of scalars. This algebra has the constant function 1 as the multiplicative identity, and is a differentiable analog of the ring of regular function
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s in algebraic geometry.
It is possible to reconstruct a manifold from its algebra of scalars, first as a set, but also as a topological space – this is an application of the Banach–Stone theorem, and is more formally known as the spectrum of a C*-algebra. First, there is a one-to-one correspondence between the points of M and the algebra homomorphisms φ : Ck(M) → R, as such a homomorphism φ corresponds a codimension one ideal in Ck(M) (namely the kernel of φ), which is necessarily a maximal ideal. On the converse, every maximal ideal in this algebra is an ideal of functions vanishing at a single point, which demonstrates that MSpec (the Max Spec) of Ck(M) recovers M as a point set, though in fact it recovers M as a topological space.
One can define various geometric structures algebraically in terms of the algebra of scalars, and these definitions often generalize to algebraic geometry (interpreting rings geometrically) and operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
(interpreting Banach spaces geometrically). For example, the tangent bundle to M can be defined as the derivations of the algebra of smooth functions on M.
This "algebraization" of a manifold (replacing a geometric object with an algebra) leads to the notion of a C*-algebra – a commutative C*-algebra being precisely the ring of scalars of a manifold, by Banach–Stone, and allows one to consider noncommutative C*-algebras as non-commutative generalizations of manifolds. This is the basis of the field of noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
.
Tangent bundle
The tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of a point consists of the possible directional derivatives at that point, and has the same dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
n as does the manifold. For a set of (non-singular) coordinates
 local to the point, the coordinate derivatives
local to the point, the coordinate derivatives  typically define a basis of the tangent space. The collection of tangent spaces at all points can in turn be made into a manifold, the tangent bundle
typically define a basis of the tangent space. The collection of tangent spaces at all points can in turn be made into a manifold, the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, whose dimension is 2n. The tangent bundle is where tangent vector
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s lie, and is itself a differentiable manifold. The Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
is a function on the tangent bundle. One can also define the tangent bundle as the bundle of 1-jets
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
from R (the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
) to M.
One may construct an atlas for the tangent bundle consisting of charts based on Uα × Rn, where Uα denotes one of the charts in the atlas for M. Each of these new charts is the tangent bundle for the charts Uα. The transition maps on this atlas are defined from the transition maps on the original manifold, and retain the original differentiability class.
Cotangent bundle
The dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of a vector space is the set of real valued linear functions on the vector space. When the space is finite dimensional the dual space will be isomorphic (as a linear space) to the original vector space, which is to say it has the same dimension. Thus the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
at a point is the dual of the tangent space at that point and the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
is the collection of all cotangent spaces.
Like the tangent bundle the cotangent bundle is again a differentiable manifold. The Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
is a scalar on the cotangent bundle. The total space of a cotangent bundle has the structure of a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. Cotangent vectors are sometimes called covectors. One can also define the cotangent bundle as the bundle of 1-jets
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
of functions from M to R.
Elements of the cotangent space can be thought of as infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
displacements: if f is a differentiable function we can define at each point p a cotangent vector dfp, which sends a tangent vector Xp to the derivative of f associated with Xp. However, not every covector field can be expressed this way.
For a given set of local (non-singular) coordinates
 the differentials
the differentials  typically define a basis of the cotangent space(s).
typically define a basis of the cotangent space(s).Tensor bundle
The tensor bundle is the direct sum of all tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of the tangent bundle and the cotangent bundle. Each element of the bundle is a tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
, which can act as a multilinear operator on vector fields, or on other tensor fields.
The tensor bundle cannot be a differentiable manifold, since it is infinite dimensional. It is however an algebra
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over the ring of scalar functions. Each tensor is characterized by its ranks, which indicate how many tangent and cotangent factors it has. Sometimes these ranks are referred to as covariant and contravariant ranks, signifying tangent and cotangent ranks, respectively.
Frame bundle
A frame (or, in more precise terms, a tangent frame) is an ordered basis of particular tangent space. Likewise, a tangent frame is a linear isomorphism of Rn to this tangent space. A moving tangent frame is an ordered list of vector fields that give a basis at every point of their domain. One may also regard a moving frame as a section of the frame bundle F(M), a GLnRGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
made up of the set of all frames over M. The frame bundle is useful because tensor fields on M can be regarded as equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
vector-valued functions on F(M).
Jet bundles
On a manifold that is sufficiently smooth, various kinds of jet bundles can also be considered. The (first-order) tangent bundle of a manifold is the collection of curves in the manifold modulo the equivalence relation of first-order contactContact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
. By analogy, the k-th order tangent bundle is the collection of curves modulo the relation of k-th order contact. Likewise, the cotangent bundle is the bundle of 1-jets of functions on the manifold: the k-jet bundle is the bundle of their k-jets. These and other examples of the general idea of jet bundles play a significant role in the study of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s on manifolds.
The notion of a frame also generalizes to the case of higher-order jets. Define a k-th order frame to be the k-jet of a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
from Rn to M. The collection of all k-th order frames, Fk(M), is a principle Gk bundle over M, where Gk is the group of k-jets
Jet group
In mathematics, a jet group is a generalization of the general linear group which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate systems .The k-th order jet group Gnk consists of jets of...
; i.e., the group made up of k-jets
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
of diffeomorphisms of Rn that fix the origin. Note that GLn (R) is naturally isomorphic to G1, and a subgroup of every Gk, k≥2. In particular, a section of F2(M) gives the frame components of a connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on M. Thus, the quotient bundle F2(M)/ GLn (R) is the bundle of linear connections over M.
Calculus on manifolds
Many of the techniques from multivariate calculus also apply, mutatis mutandisMutatis mutandis
Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....
, to differentiable manifolds. One can define the directional derivative of a differentiable function along a tangent vector to the manifold, for instance, and this leads to a means of generalizing the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of a function: the differential. From the perspective of calculus, the derivative of a function on a manifold behaves in much the same way as the ordinary derivative of a function defined on a Euclidean space, at least locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
. For example, there are versions of the implicit
Implicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
and inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
s for such functions.
There are, however, important differences in the calculus of vector fields (and tensor fields in general). In brief, the directional derivative of a vector field is not well-defined, or at least not defined in a straightforward manner. Several generalizations of the derivative of a vector field (or tensor field) do exist, and capture certain formal features of differentiation in Euclidean spaces. The chief among these are:
- The Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
, which is uniquely defined by the differential structure, but fails to satisfy some of the usual features of directional differentiation. - An affine connectionAffine connectionIn the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, which is not uniquely defined, but generalizes in a more complete manner the features of ordinary directional differentiation. Because an affine connection is not unique, it is an additional piece of data that must be specified on the manifold.
Ideas from integral calculus also carry over to differential manifolds. These are naturally expressed in the language of exterior calculus and differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. The fundamental theorems of integral calculus in several variables — namely Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
, the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, and Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
— generalize to a theorem (also called Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
) relating the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
and integration over submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s.
Differential calculus of functions
Differentiable functions between two manifolds are needed in order to formulate suitable notions of submanifoldSubmanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s, and other related concepts. If f : M → N is a differentiable function from a differentiable manifold M of dimension m to another differentiable manifold N of dimension n, then the differential of f is a mapping df : TM → TN. At each point of M, this is a linear transformation from one tangent space to another:

The rank of f at p is the rank of this linear transformation.
Usually the rank of a function is a pointwise property. However, if the function has maximal rank, then the rank will remain constant in a neighborhood of a point. A differentiable function "usually" has maximal rank, in a precise sense given by Sard's theorem. Functions of maximal rank at a point are called immersions and submersions
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
:
- If m ≤ n, and f : M → N has rank m at p ∈ M, then f is called an immersion at p. If f is an immersion at all points of M and is a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
onto its image, then f is an embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
. Embeddings formalize the notion of M being a submanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of N. In general, an embedding is an immersion without self-intersections and other sorts of non-local topological irregularities.
- If m ≥ n, and f : M → N has rank n at p ∈ M, then f is called a submersion at p. The implicit function theorem states that if f is a submersion at p, then M is locally a product of N and Rm−n near p. In formal terms, there exist coordinates (y1,...,yn) in a neighborhood of f(p) in N, and m − n functions x1,...,xm−n defined in a neighborhood of p in M such that
-
- is a system of local coordinates of M in a neighborhood of p. Submersions form the foundation of the theory of fibrationFibrationIn topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s and fibre bundles.
Lie derivative
A Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
, named after Sophus Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
, is a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
on the algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s over a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M. The vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all Lie derivatives on M forms an infinite dimensional Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
with respect to the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
defined by

The Lie derivatives are represented by vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, as infinitesimal generators of flows (active diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s) on M. Looking at it the other way round, the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of diffeomorphisms of M has the associated Lie algebra structure, of Lie derivatives, in a way directly analogous to the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory.
Exterior calculus
The exterior calculus allows for a generalization of the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and curl operators.
The bundle of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s, at each point, consists of all totally antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
multilinear maps on the tangent space at that point. It is naturally divided into n-forms for each n at most equal to the dimension of the manifold; an n-form is an n-variable form, also called a form of degree n. The 1-forms are the cotangent vectors, while the 0-forms are just scalar functions. In general, an n-form is a tensor with cotangent rank n and tangent rank 0. But not every such tensor is a form, as a form must be antisymmetric.
Exterior derivative
There is a map from scalars to covectors called the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....

such that

This map is the one that relates covectors to infinitesimal displacements, mentioned above; some covectors are the exterior derivatives of scalar functions. It can be generalized into a map from the n-forms onto the n+1-forms. Applying this derivative twice will produce a zero form. Forms with zero derivative are called closed forms, while forms that are themselves exterior derivatives are known as exact forms.
The space of differential forms at a point is the archetypal example of an exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
; thus it possesses a wedge product, mapping a k-form and l-form to a k+l-form. The exterior derivative extends to this algebra, and satisfies a version of the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
:
From the differential forms and the exterior derivative, one can define the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
of the manifold. The rank n cohomology group is the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of the closed forms by the exact forms.
Relationship with topological manifolds
Every topological manifold in dimension 1, 2, or 3 has a unique differential structure (up to diffeomorphism); thus the concepts of topological and differentiable manifold are distinct only in higher dimensions. It is known that in each higher dimension, there are some topological manifolds with no smooth structure, and some with multiple non-diffeomorphic structures.The existence of non-smoothable manifolds was proven by , and later explained in the context of Donaldson's theorem
Donaldson's theorem
In mathematics, Donaldson's theorem states that a definite intersection form of a simply connected smooth manifold of dimension 4 is diagonalisable. If the intersection form is positive definite, it can be diagonalized to the identity matrix...
(compare Hilbert's fifth problem
Hilbert's fifth problem
Hilbert's fifth problem, is the fifth mathematical problem from the problem-list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics...
); a good example of a non-smoothable manifold is the E8 manifold
E8 manifold
In mathematics, the E8 manifold is the unique compact, simply connected topological 4-manifold with intersection form the E8 lattice.The E8 manifold was discovered by Michael Freedman in 1982...
.
The classic example of manifolds with multiple incompatible structures are the exotic 7-spheres
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
of John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
.
Classification
Every second-countable 1-manifold without boundary is homeomorphic to a disjoint union of countably many copies of R (the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
) and S (the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
); the only connected examples are R and S, and of these only S is compact. In higher dimensions, classification theory normally focuses only on compact connected manifolds.
For a classification of 2-manifolds, see surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
: in particular compact connected oriented 2-manifolds are classified by their genus, which is a nonnegative integer.
A classification of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s follows in principle from the geometrization of 3-manifolds and various recognition results for geometrizable 3-manifolds, such as Mostow rigidity and Sela's algorithm for the isomorphism problem for hyperbolic groups.
The classification of n-manifolds for n greater than three is known to be impossible, even up to homotopy equivalence. Given any finitely presented
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
group, one can construct a closed 4-manifold having that group as fundamental group. Since there is no algorithm to decide
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
the isomorphism problem for finitely presented groups, there is no algorithm to decide if two 4-manifolds have the same fundamental group. Since the previously described construction results in a class of 4-manifolds that are homeomorphic if and only if their groups are isomorphic, the homeomorphism problem for 4-manifolds is undecidable
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
. In addition, since even recognizing the trivial group is undecidable, it is not even possible in general to decide if a manifold has trivial fundamental group, i.e. is simply connected.
Simply connected 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
s have been classified up to homeomorphism by Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
using the intersection form
Intersection form
Intersection form may refer to:*Intersection theory *intersection form...
and Kirby–Siebenmann invariant. Smooth 4-manifold theory is known to be much more complicated, as the exotic smooth structure
Exotic R4
In mathematics, an exotic R4 is a differentiable manifold that is homeomorphic to the Euclidean space R4, but not diffeomorphic.The first examples were found by Robion Kirby and Michael Freedman, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's...
s on
 demonstrate.
demonstrate.However, the situation becomes more tractable for simply connected smooth manifolds of dimension ≥ 5, where the h-cobordism theorem can be used to reduce the classification to a classification up to homotopy equivalence, and surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
can be applied. This has been carried out to provide an explicit classification of simply connected 5-manifold
5-manifold
In mathematics, a 5-manifold is a 5-dimensional topological manifold, possibly with a piecewise linear or smooth structure.Non-simply connected 5-manifolds are impossible to classify, as this is harder than solving the word problem for groups. Simply connected compact 5-manifolds were first...
s by Dennis Barden.
(Pseudo-)Riemannian manifolds
A Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
is a differentiable manifold on which the tangent spaces are equipped with inner products
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
in a differentiable fashion. The inner product structure is given in the form of a symmetric 2-tensor called the Riemannian metric. This metric can be used to interconvert vectors and covectors, and to define a rank 4 Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. On a Riemannian manifold one has notions of length, volume, and angle. Any differentiable manifold can be given a Riemannian structure.
A pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
is a variant of Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
where the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is allowed to have an indefinite signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(as opposed to a positive-definite one). Pseudo-Riemannian manifolds of signature (3, 1) are important in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Not every differentiable manifold can be given a pseudo-Riemannian structure; there are topological restrictions on doing so.
A Finsler manifold
Finsler manifold
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
is a generalization of a Riemannian manifold, in which the inner product is replaced with a vector norm; this allows the definition of length, but not angle.
Symplectic manifolds
A symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
is a manifold equipped with a closed, nondegenerate 2-form. This condition forces symplectic manifolds to be even-dimensional. Cotangent bundles, which arise as phase spaces in Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, are the motivating example, but many compact manifolds also have symplectic structure. All orientable surfaces embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
have a symplectic structure, the signed area form on each tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
induced by the ambient Euclidean inner product.This form is clearly nondegenerate, and it must be closed because it is top-dimensional with respect to the surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
; this reflects the exceptional isomorphism
Exceptional isomorphism
In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members ai and bj of two families of mathematical objects, that is not an example of a pattern of such isomorphisms.Because these series of objects are presented differently, they are not...
of Lie groups
 between the symplectic group
between the symplectic groupSymplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
(corresponding to symplectic structure) and the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
(corresponding to orientable structure). Note that a symplectic structure requires an additional integrability condition, beyond this isomorphism of groups: it is not just a G-structure
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
. Every Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is an example of such a surface, and hence a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
, when considered as a real manifold.
Lie groups
A Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is C∞ manifold that also carries a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
structure whose product and inversion operations are smooth as maps of manifolds. These objects arise naturally in describing symmetries.
Generalizations
The categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of smooth manifolds with smooth maps lacks certain desirable properties, and people have tried to generalize smooth manifolds in order to rectify this. The diffeological spaces, (differential spaces) use a different notion of chart known as "plot". Frölicher space
Frölicher space
In mathematics, Frölicher spaces extend the notions of calculus and smooth manifolds. They were introduced in 1982 by the mathematician Alfred Frölicher.-Definition:...
s and orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
s are other attempts.
A rectifiable set
Rectifiable set
In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
generalizes the idea of a piece-wise smooth or rectifiable curve to higher dimensions; however, rectifiable sets are not in general manifolds.
See also
- Affine connectionAffine connectionIn the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
- Atlas (topology)Atlas (topology)In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
- Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
- Differential geometry
- Introduction to mathematics of general relativity
- List of formulas in Riemannian geometry
- Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
- Space (mathematics)




