.gif)
Connection (mathematics)
Encyclopedia
In geometry
, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport. For instance, an affine connection
, the most elementary type of connection, gives a means for transporting tangent vectors
to a manifold
from one point to another along a curve. An affine connection is typically given in the form of a covariant derivative
, which gives a means for taking directional derivative
s of vector fields: the infinitesimal transport of a vector field
in a given direction.
Connections are of central importance in modern geometry in large part because they allow a comparison between the local geometry at one point and the local geometry at another point. Differential geometry embraces several variations on the connection theme, which fall into two major groups: the infinitesimal and the local theory. The local theory concerns itself primarily with notions of parallel transport
and holonomy
. The infinitesimal theory concerns itself with the differentiation of geometric data. Thus a covariant derivative is a way of specifying a derivative
of a vector field along another vector field on a manifold. A Cartan connection
is a way of formulating some aspects of connection theory using differential forms and Lie group
s. An Ehresmann connection
is a connection in a fibre bundle or a principal bundle
by specifying the allowed directions of motion of the field. A Koszul connection is a connection generalizing the derivative in a vector bundle
.
Connections also lead to convenient formulations of geometric invariants, such as the curvature
(see also curvature tensor
and curvature form
), and torsion tensor
.
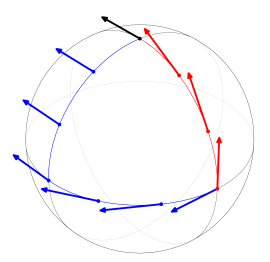Consider the following problem. Suppose that a tangent vector to the sphere S is given at the north pole, and we are to define a manner of consistently moving this vector to other points of the sphere: a means for parallel transport. Naïvely, this could be done using a particular coordinate system
. However, unless proper care is applied, the parallel transport defined in one system of coordinates will not agree with that of another coordinate system. A more appropriate parallel transportation system exploits the symmetry of the sphere under rotation. Given a vector at the north pole, one can transport this vector along a curve by rotating the sphere in such a way that the north pole moves along the curve without axial rolling. This latter means of parallel transport is the Levi-Civita connection
on the sphere. If two different curves are given with the same initial and terminal point, and a vector v is rigidly moved along the first curve by a rotation, the resulting vector at the terminal point will be different from the vector resulting from rigidly moving v along the second curve. This phenomenon reflects the curvature
of the sphere. A simple mechanical device that can be used to visualize parallel transport is the South Pointing Chariot
.
For instance, suppose that S is given coordinates by the stereographic projection
. Regard S as consisting of unit vectors in R3. Then S carries a pair of coordinate patches: one covering a neighborhood of the north pole, and the other of the south pole. The mappings
cover a neighborhood U0 of the north pole and U1 of the south pole, respectively. Let X, Y, Z be the ambient coordinates in R3. Then φ0 and φ1 have inverses
so that the coordinate transition function is inversion in the circle:
Let us now represent a vector field in terms of its components relative to the coordinate derivatives. If P is a point of U0 ⊂ S, then a vector field may be represented by
where
denotes the Jacobian matrix of φ0, and v0 = v0(x, y) is a vector field on R2 uniquely determined by v. Furthermore, on the overlap between the coordinate charts U0 ∩ U1, it is possible to represent the same vector field with respect to the φ1 coordinates:
To relate the components v0 and v1, apply the chain rule
to the identity φ1 = φ0 o φ01:
Applying both sides of this matrix equation to the component vector v1(φ1−1(P)) and invoking (1) and (2) yields
We come now to the main question of defining how to transport a vector field parallelly along a curve. Suppose that P(t) is a curve in S. Naïvely, one may consider a vector field parallel if the coordinate components of the vector field are constant along the curve. However, an immediate ambiguity arises: in which coordinate system should these components be constant?
For instance, suppose that v(P(t)) has constant components in the U1 coordinate system. That is, the functions v1(φ1−1(P(t))) are constant. However, applying the product rule
to (3) and using the fact that dv1/dt = 0 gives
But
is always a non-singular matrix (provided that the curve P(t) is not stationary), so v1 and v0 cannot ever be simultaneously constant along the curve.
of vector calculus does not behave well under changes in the coordinate system when applied to the components of vector fields. This makes it quite difficult to describe how to parallelly translate vector fields, if indeed such a notion makes any sense at all. There are two fundamentally different ways of resolving this problem.
The first approach is to examine what is required for a generalization of the directional derivative to "behave well" under coordinate transitions. This is the tactic taken by the covariant derivative
approach to connections: good behavior is equated with covariance. Here one considers a modification of the directional derivative by a certain linear operator, whose components are called the Christoffel symbols
, which involves no derivatives on the vector field itself. The directional derivative Duv of the components of a vector v in a coordinate system φ in the direction u are replaced by a covariant derivative:
where Γ depends on the coordinate system φ and is bilinear
in u and v. In particular, Γ does not involve any derivatives on u or v. In this approach, Γ must transform in a prescribed manner when the coordinate system φ is changed to a different coordinate system. This transformation is not tensor
ial, since it involves not only the first derivative of the coordinate transition, but also its second derivative. Specifying the transformation law of Γ is not sufficient to determine Γ uniquely. Some other normalization conditions must be imposed, usually depending on the type of geometry under consideration. In Riemannian geometry
, the Levi-Civita connection
requires compatibility of the Christoffel symbols
with the metric (as well as a certain symmetry condition). With these normalizations, the connection is uniquely defined.
The second approach is to use Lie group
s to attempt to capture some vestige of symmetry on the space. This is the approach of Cartan connection
s. The example above using rotations to specify the parallel transport of vectors on the sphere is very much in this vein.
perspective in Riemannian geometry
. The infinitesimal study of connections began to some extent with Christoffel. This was later taken up more thoroughly by Gregorio Ricci-Curbastro
and Tullio Levi-Civita
who observed in part that a connection in the infinitesimal sense of Christoffel also allowed for a notion of parallel transport
.
The work of Levi-Civita focused exclusively on regarding connections as a kind of differential operator
whose parallel displacements were then the solutions of differential equation
s. As the twentieth century progressed, Élie Cartan
developed a new notion of connection. He sought to apply the techniques of Pfaffian systems to the geometries of Felix Klein
's Erlangen program
. In these investigations, he found that a certain infinitesimal notion of connection (a Cartan connection
) could be applied to these geometries and more: his connection concept allowed for the presence of curvature
which would otherwise be absent in a classical Klein geometry. (See, for example, and .) Furthermore, using the dynamics of Gaston Darboux, Cartan was able to generalize the notion of parallel transport for his class of infinitesimal connections. This established another major thread in the theory of connections: that a connection is a certain kind of differential form
.
The two threads in connection theory have persisted through the present day: a connection as a differential operator, and a connection as a differential form. In 1950, Jean-Louis Koszul
gave an algebraic framework for regarding a connection as a differential operator by means of the Koszul connection. The Koszul connection was both more general than that of Levi-Civita, and was easier to work with because it finally was able to eliminate (or at least to hide) the awkward Christoffel symbols
from the connection formalism. The attendant parallel displacement operations also had natural algebraic interpretations in terms of the connection. Koszul's definition was subsequently adopted by most of the differential geometry community, since it effectively converted the analytic correspondence between covariant differentiation and parallel translation to an algebraic one.
In that same year, Charles Ehresmann
, a student of Cartan's, presented a variation on the connection as a differential form view in the context of principal bundle
s and, more generally, fibre bundles. Ehresmann connection
s were, strictly speaking, not a generalization of Cartan connections. Cartan connections were quite rigidly tied to the underlying differential topology
of the manifold because of their relationship with Cartan's equivalence method
. Ehresmann connections were rather a solid framework for viewing the foundational work of other geometers of the time, such as Shiing-Shen Chern
, who had already begun moving away from Cartan connections to study what might be called gauge connections. In Ehresmann's point of view, a connection in a principal bundle consists of a specification of horizontal and vertical vector fields on the total space of the bundle. A parallel translation is then a lifting of a curve from the base to a curve in the principal bundle which is horizontal. This viewpoint has proven especially valuable in the study of holonomy
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport. For instance, an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, the most elementary type of connection, gives a means for transporting tangent vectors
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
from one point to another along a curve. An affine connection is typically given in the form of a covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
, which gives a means for taking directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
s of vector fields: the infinitesimal transport of a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
in a given direction.
Connections are of central importance in modern geometry in large part because they allow a comparison between the local geometry at one point and the local geometry at another point. Differential geometry embraces several variations on the connection theme, which fall into two major groups: the infinitesimal and the local theory. The local theory concerns itself primarily with notions of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
and holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
. The infinitesimal theory concerns itself with the differentiation of geometric data. Thus a covariant derivative is a way of specifying a derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a vector field along another vector field on a manifold. A Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
is a way of formulating some aspects of connection theory using differential forms and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. An Ehresmann connection
Ehresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
is a connection in a fibre bundle or a principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
by specifying the allowed directions of motion of the field. A Koszul connection is a connection generalizing the derivative in a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
.
Connections also lead to convenient formulations of geometric invariants, such as the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
(see also curvature tensor
Curvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
and curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
), and torsion tensor
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
.
Motivation: the unsuitability of coordinates
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. However, unless proper care is applied, the parallel transport defined in one system of coordinates will not agree with that of another coordinate system. A more appropriate parallel transportation system exploits the symmetry of the sphere under rotation. Given a vector at the north pole, one can transport this vector along a curve by rotating the sphere in such a way that the north pole moves along the curve without axial rolling. This latter means of parallel transport is the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
on the sphere. If two different curves are given with the same initial and terminal point, and a vector v is rigidly moved along the first curve by a rotation, the resulting vector at the terminal point will be different from the vector resulting from rigidly moving v along the second curve. This phenomenon reflects the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the sphere. A simple mechanical device that can be used to visualize parallel transport is the South Pointing Chariot
South Pointing Chariot
The south-pointing chariot was an ancient Chinese two-wheeled vehicle that carried a movable pointer to indicate the south, no matter how the chariot turned. Usually, the pointer took the form of a doll or figure with an outstretched arm...
.
For instance, suppose that S is given coordinates by the stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. Regard S as consisting of unit vectors in R3. Then S carries a pair of coordinate patches: one covering a neighborhood of the north pole, and the other of the south pole. The mappings
cover a neighborhood U0 of the north pole and U1 of the south pole, respectively. Let X, Y, Z be the ambient coordinates in R3. Then φ0 and φ1 have inverses
so that the coordinate transition function is inversion in the circle:
Let us now represent a vector field in terms of its components relative to the coordinate derivatives. If P is a point of U0 ⊂ S, then a vector field may be represented by
where
denotes the Jacobian matrix of φ0, and v0 = v0(x, y) is a vector field on R2 uniquely determined by v. Furthermore, on the overlap between the coordinate charts U0 ∩ U1, it is possible to represent the same vector field with respect to the φ1 coordinates:To relate the components v0 and v1, apply the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
to the identity φ1 = φ0 o φ01:
Applying both sides of this matrix equation to the component vector v1(φ1−1(P)) and invoking (1) and (2) yields
We come now to the main question of defining how to transport a vector field parallelly along a curve. Suppose that P(t) is a curve in S. Naïvely, one may consider a vector field parallel if the coordinate components of the vector field are constant along the curve. However, an immediate ambiguity arises: in which coordinate system should these components be constant?
For instance, suppose that v(P(t)) has constant components in the U1 coordinate system. That is, the functions v1(φ1−1(P(t))) are constant. However, applying the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
to (3) and using the fact that dv1/dt = 0 gives
But
is always a non-singular matrix (provided that the curve P(t) is not stationary), so v1 and v0 cannot ever be simultaneously constant along the curve.Resolution
The problem observed above is that the usual directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of vector calculus does not behave well under changes in the coordinate system when applied to the components of vector fields. This makes it quite difficult to describe how to parallelly translate vector fields, if indeed such a notion makes any sense at all. There are two fundamentally different ways of resolving this problem.
The first approach is to examine what is required for a generalization of the directional derivative to "behave well" under coordinate transitions. This is the tactic taken by the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
approach to connections: good behavior is equated with covariance. Here one considers a modification of the directional derivative by a certain linear operator, whose components are called the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
, which involves no derivatives on the vector field itself. The directional derivative Duv of the components of a vector v in a coordinate system φ in the direction u are replaced by a covariant derivative:
where Γ depends on the coordinate system φ and is bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
in u and v. In particular, Γ does not involve any derivatives on u or v. In this approach, Γ must transform in a prescribed manner when the coordinate system φ is changed to a different coordinate system. This transformation is not tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
ial, since it involves not only the first derivative of the coordinate transition, but also its second derivative. Specifying the transformation law of Γ is not sufficient to determine Γ uniquely. Some other normalization conditions must be imposed, usually depending on the type of geometry under consideration. In Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
requires compatibility of the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
with the metric (as well as a certain symmetry condition). With these normalizations, the connection is uniquely defined.
The second approach is to use Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s to attempt to capture some vestige of symmetry on the space. This is the approach of Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
s. The example above using rotations to specify the parallel transport of vectors on the sphere is very much in this vein.
Historical survey of connections
Historically, connections were studied from an infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
perspective in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. The infinitesimal study of connections began to some extent with Christoffel. This was later taken up more thoroughly by Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
and Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
who observed in part that a connection in the infinitesimal sense of Christoffel also allowed for a notion of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
.
The work of Levi-Civita focused exclusively on regarding connections as a kind of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
whose parallel displacements were then the solutions of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. As the twentieth century progressed, Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
developed a new notion of connection. He sought to apply the techniques of Pfaffian systems to the geometries of Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
. In these investigations, he found that a certain infinitesimal notion of connection (a Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
) could be applied to these geometries and more: his connection concept allowed for the presence of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
which would otherwise be absent in a classical Klein geometry. (See, for example, and .) Furthermore, using the dynamics of Gaston Darboux, Cartan was able to generalize the notion of parallel transport for his class of infinitesimal connections. This established another major thread in the theory of connections: that a connection is a certain kind of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
.
The two threads in connection theory have persisted through the present day: a connection as a differential operator, and a connection as a differential form. In 1950, Jean-Louis Koszul
Jean-Louis Koszul
Jean-Louis Koszul is a mathematician best known for studying geometry and discovering the Koszul complex.He was educated at the Lycée Fustel-de-Coulanges in Strasbourg before studying at the Faculty of Science in Strasbourg and the Faculty of Science in Paris...
gave an algebraic framework for regarding a connection as a differential operator by means of the Koszul connection. The Koszul connection was both more general than that of Levi-Civita, and was easier to work with because it finally was able to eliminate (or at least to hide) the awkward Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
from the connection formalism. The attendant parallel displacement operations also had natural algebraic interpretations in terms of the connection. Koszul's definition was subsequently adopted by most of the differential geometry community, since it effectively converted the analytic correspondence between covariant differentiation and parallel translation to an algebraic one.
In that same year, Charles Ehresmann
Charles Ehresmann
Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...
, a student of Cartan's, presented a variation on the connection as a differential form view in the context of principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s and, more generally, fibre bundles. Ehresmann connection
Ehresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
s were, strictly speaking, not a generalization of Cartan connections. Cartan connections were quite rigidly tied to the underlying differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
of the manifold because of their relationship with Cartan's equivalence method
Cartan's equivalence method
In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism...
. Ehresmann connections were rather a solid framework for viewing the foundational work of other geometers of the time, such as Shiing-Shen Chern
Shiing-Shen Chern
Shiing-Shen Chern was a Chinese American mathematician, one of the leaders in differential geometry of the twentieth century.-Early years in China:...
, who had already begun moving away from Cartan connections to study what might be called gauge connections. In Ehresmann's point of view, a connection in a principal bundle consists of a specification of horizontal and vertical vector fields on the total space of the bundle. A parallel translation is then a lifting of a curve from the base to a curve in the principal bundle which is horizontal. This viewpoint has proven especially valuable in the study of holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
.
Possible approaches
- A rather direct approach is to specify how a covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
acts on elements of the moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s as a differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. More generally, a similar approach applies for connectionsConnection (vector bundle)In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
in any vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
. - Traditional index notation specifies the connection by components; see Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
. (Note: this has three indices, but is not a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
). - In pseudo-Riemannian and Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
the Levi-Civita connectionLevi-Civita connectionIn Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
is a special connection associated to the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. - These are examples of affine connectionAffine connectionIn the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
s. There is also a concept of projective connectionProjective connectionIn differential geometry, a projective connection is a type of Cartan connection on a differentiable manifold.The structure of a projective connection is modeled on the geometry of projective space, rather than the affine space corresponding to an affine connection. Much like affine connections,...
, of which the Schwarzian derivativeSchwarzian derivativeIn mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and...
in complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
is an instance. More generally, both affine and projective connections are types of Cartan connectionCartan connectionIn the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
s. - Using principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, a connection can be realized as a Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
-valued differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
. See connection (principal bundle)Connection (principal bundle)In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
. - An approach to connections which makes direct use of the notion of transport of "data" (whatever that may be) is the Ehresmann connectionEhresmann connectionIn differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
. - The most abstract approach may be that suggested by Alexander GrothendieckAlexander GrothendieckAlexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, where a Grothendieck connectionGrothendieck connectionIn algebraic geometry and synthetic differential geometry, a Grothendieck connection is a way of viewing connections in terms of descent data from infinitesimal neighbourhoods of the diagonal.-Introduction and motivation:...
is seen as descentDescent (category theory)In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...
data from infinitesimal neighbourhoods of the diagonalDiagonalA diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
; see .