
Implicit function
Encyclopedia
The implicit function theorem
provides a link between implicit and explicit functions. It states that if the equation R(x, y) = 0 satisfies some mild conditions on its partial derivative
s, then one can in principle solve this equation for y, at least over some small interval
. Geometrically, the graph defined by R(x,y) = 0 will overlap locally
with the graph of an equation y = f(x).
Various numerical methods exist for solving the equation R(x,y)=0 to find an approximation to the implicit function f. Many of these methods are iterative in that they produce successively better approximations, so that a prescribed accuracy can be achieved. Many of these iterative methods are based on some form of Newton's method
.
. If is a function, then the inverse function of
is a function, then the inverse function of  , called
, called 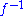 , is the function giving a solution of the equation
, is the function giving a solution of the equation
for y in terms of x. This solution is
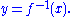
Intuitively, an inverse function is obtained from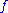 by interchanging the roles of the dependent and independent variables. Stated another way, the inverse function gives the solution for y of the equation
by interchanging the roles of the dependent and independent variables. Stated another way, the inverse function gives the solution for y of the equation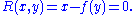
Examples.
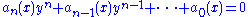
where the coefficients are polynomial functions of x. Algebraic functions play an important role in mathematical analysis
are polynomial functions of x. Algebraic functions play an important role in mathematical analysis
and algebraic geometry
. A simple example of an algebraic function is given by the unit circle equation: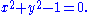
Solving for y gives an explicit solution: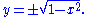
But even without specifying this explicit solution, it is possible to refer to the implicit solution of the unit circle equation.
While explicit solutions can be found for equations that are quadratic, cubic, and quartic in y, the same is not in general true for quintic
and higher degree equations, such as
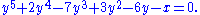
Nevertheless, one can still refer to the implicit solution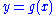 involving the multi-valued implicit function
involving the multi-valued implicit function  .
.
The defining equation can also have other pathologies. For example, the equation x = 0 does not imply a function
can also have other pathologies. For example, the equation x = 0 does not imply a function  giving solutions for y at all; it is a vertical line. In order to avoid a problem like this, various constraints are frequently imposed on the allowable sorts of equations or on the domain. The implicit function theorem provides a uniform way of handling these sorts of pathologies.
giving solutions for y at all; it is a vertical line. In order to avoid a problem like this, various constraints are frequently imposed on the allowable sorts of equations or on the domain. The implicit function theorem provides a uniform way of handling these sorts of pathologies.
, a method called implicit differentiation makes use of the chain rule
to differentiate implicitly defined functions.
As explained in the introduction, y can be given as a function of x implicitly rather than explicitly. When we have an equation R(x, y) = 0, we may be able to solve it for y and then
differentiate. However, sometimes it is simpler to differentiate R(x, y) with respect to x and y and then solve for dy/dx.

This function normally can be manipulated by using algebra
to change this equation
to one expressing y in terms of an explicit function
:
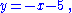
where the right side is the explicit function whose output value is y. Differentiation then gives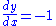 . Alternatively, one can totally differentiate the original equation:
. Alternatively, one can totally differentiate the original equation:
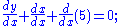

Solving for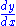 gives:
gives:

the same answer as obtained previously.
2. An example of an implicit function, for which implicit differentiation might be easier than attempting to use explicit differentiation, is
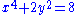
In order to differentiate this explicitly with respect to x, one would have to obtain (via algebra)
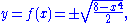
and then differentiate this function. This creates two derivatives: one for y > 0 and another for y < 0.
One might find it substantially easier to implicitly differentiate the original function:
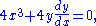
giving,
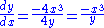
3. Sometimes standard explicit differentiation cannot be used and, in order to obtain the derivative, implicit differentiation must be employed. An example of such a case is the equation y5 − y = x. It is impossible to express y explicitly as a function of x and therefore dy/dx cannot be found by explicit differentiation. Using the implicit method, dy/dx can be expressed:
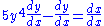
where Factoring out
Factoring out  shows that
shows that

which yields the final answer
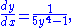
which is defined for
 is defined on an open disk containing
is defined on an open disk containing  , where
, where  ,
, 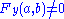 , and
, and 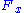 and
and 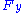 are continuous on the disk, then the equation
are continuous on the disk, then the equation  defines
defines 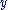 as a function of
as a function of  near the point
near the point  and the derivative of this function is given by..."
and the derivative of this function is given by..."
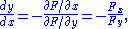
where and
and  indicate the derivatives of
indicate the derivatives of 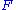 with respect to x and y.
with respect to x and y.
The above formula comes from using the generalized chain rule to obtain the total derivative
—with respect to x—of both sides of F(x, y) = 0:

and hence

 is given by a smooth submanifold
is given by a smooth submanifold
 in
in 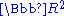 , and
, and  is a point of this submanifold such that the tangent space
is a point of this submanifold such that the tangent space
there is not vertical (that is ), then
), then  in some small enough neighbourhood
in some small enough neighbourhood
of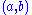 is given by a parametrization
is given by a parametrization
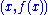 where
where 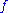 is a smooth function
is a smooth function
. In less technical language, implicit functions exist and can be differentiated, unless the tangent to the supposed graph would be vertical. In the standard case where we are given an equation

the condition on can be checked by means of partial derivative
can be checked by means of partial derivative
s.
, when the level set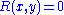 is an indifference curve
is an indifference curve
for the quantities x and y consumed of two goods, the absolute value of the implicit derivative is interpreted as the marginal rate of substitution
of the two goods: how much more of y one must receive in order to be indifferent to a loss of 1 unit of x.
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
provides a link between implicit and explicit functions. It states that if the equation R(x, y) = 0 satisfies some mild conditions on its partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s, then one can in principle solve this equation for y, at least over some small interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
. Geometrically, the graph defined by R(x,y) = 0 will overlap locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
with the graph of an equation y = f(x).
Various numerical methods exist for solving the equation R(x,y)=0 to find an approximation to the implicit function f. Many of these methods are iterative in that they produce successively better approximations, so that a prescribed accuracy can be achieved. Many of these iterative methods are based on some form of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
.
Inverse functions
A common type of implicit function is an inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
. If
 is a function, then the inverse function of
is a function, then the inverse function of  , called
, called 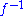 , is the function giving a solution of the equation
, is the function giving a solution of the equation
for y in terms of x. This solution is
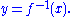
Intuitively, an inverse function is obtained from
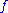 by interchanging the roles of the dependent and independent variables. Stated another way, the inverse function gives the solution for y of the equation
by interchanging the roles of the dependent and independent variables. Stated another way, the inverse function gives the solution for y of the equation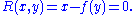
Examples.
- The natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
ln(x) gives the solution y = ln(x) of the equation x − ey = 0 or equivalently of x = ey. Here and
and 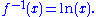
- The product log is an implicit function giving the solution for y of the equation x − y ey = 0.
Algebraic functions
An algebraic function is a function that satisfies a polynomial equation whose coefficients are themselves polynomials. For example, an algebraic function in one variable x gives a solution for y of an equation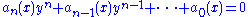
where the coefficients
 are polynomial functions of x. Algebraic functions play an important role in mathematical analysis
are polynomial functions of x. Algebraic functions play an important role in mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. A simple example of an algebraic function is given by the unit circle equation:
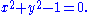
Solving for y gives an explicit solution:
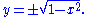
But even without specifying this explicit solution, it is possible to refer to the implicit solution of the unit circle equation.
While explicit solutions can be found for equations that are quadratic, cubic, and quartic in y, the same is not in general true for quintic
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
and higher degree equations, such as
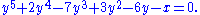
Nevertheless, one can still refer to the implicit solution
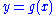 involving the multi-valued implicit function
involving the multi-valued implicit function  .
.Caveats
Not every equation R(x, y) = 0 implies a graph of a single-valued function, the circle equation being one prominent example. Another example is an implicit function given by x − C(y) = 0 where C is a cubic polynomial having a "hump" in its graph. Thus, for an implicit function to be a true (single-valued) function it might be necessary to use just part of the graph. An implicit function can sometimes be successfully defined as a true function only after "zooming in" on some part of the x-axis and "cutting away" some unwanted function branches. Then an equation expressing y as an implicit function of the other variable(s) can be written.The defining equation
 can also have other pathologies. For example, the equation x = 0 does not imply a function
can also have other pathologies. For example, the equation x = 0 does not imply a function  giving solutions for y at all; it is a vertical line. In order to avoid a problem like this, various constraints are frequently imposed on the allowable sorts of equations or on the domain. The implicit function theorem provides a uniform way of handling these sorts of pathologies.
giving solutions for y at all; it is a vertical line. In order to avoid a problem like this, various constraints are frequently imposed on the allowable sorts of equations or on the domain. The implicit function theorem provides a uniform way of handling these sorts of pathologies.Implicit differentiation
In calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, a method called implicit differentiation makes use of the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
to differentiate implicitly defined functions.
As explained in the introduction, y can be given as a function of x implicitly rather than explicitly. When we have an equation R(x, y) = 0, we may be able to solve it for y and then
differentiate. However, sometimes it is simpler to differentiate R(x, y) with respect to x and y and then solve for dy/dx.
Examples
1. Consider for example
This function normally can be manipulated by using algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
to change this equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
to one expressing y in terms of an explicit function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
:
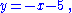
where the right side is the explicit function whose output value is y. Differentiation then gives
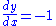 . Alternatively, one can totally differentiate the original equation:
. Alternatively, one can totally differentiate the original equation: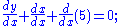

Solving for
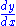 gives:
gives:
the same answer as obtained previously.
2. An example of an implicit function, for which implicit differentiation might be easier than attempting to use explicit differentiation, is
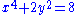
In order to differentiate this explicitly with respect to x, one would have to obtain (via algebra)
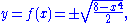
and then differentiate this function. This creates two derivatives: one for y > 0 and another for y < 0.
One might find it substantially easier to implicitly differentiate the original function:
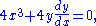
giving,
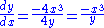
3. Sometimes standard explicit differentiation cannot be used and, in order to obtain the derivative, implicit differentiation must be employed. An example of such a case is the equation y5 − y = x. It is impossible to express y explicitly as a function of x and therefore dy/dx cannot be found by explicit differentiation. Using the implicit method, dy/dx can be expressed:
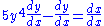
where
 Factoring out
Factoring out  shows that
shows that
which yields the final answer
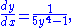
which is defined for

Formula for two variables
"The Implicit Function Theorem states that if is defined on an open disk containing
is defined on an open disk containing  , where
, where  ,
, 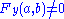 , and
, and 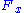 and
and 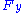 are continuous on the disk, then the equation
are continuous on the disk, then the equation  defines
defines 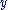 as a function of
as a function of  near the point
near the point  and the derivative of this function is given by..."
and the derivative of this function is given by..."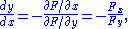
where
 and
and  indicate the derivatives of
indicate the derivatives of 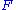 with respect to x and y.
with respect to x and y.The above formula comes from using the generalized chain rule to obtain the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
—with respect to x—of both sides of F(x, y) = 0:

and hence

Implicit function theorem
It can be shown that if is given by a smooth submanifold
is given by a smooth submanifoldSubmanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
 in
in 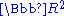 , and
, and  is a point of this submanifold such that the tangent space
is a point of this submanifold such that the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
there is not vertical (that is
 ), then
), then  in some small enough neighbourhood
in some small enough neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of
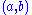 is given by a parametrization
is given by a parametrizationParametrization
Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....
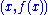 where
where 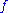 is a smooth function
is a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. In less technical language, implicit functions exist and can be differentiated, unless the tangent to the supposed graph would be vertical. In the standard case where we are given an equation

the condition on
 can be checked by means of partial derivative
can be checked by means of partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s.
Marginal rate of substitution
In economicsEconomics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, when the level set
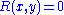 is an indifference curve
is an indifference curveIndifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
for the quantities x and y consumed of two goods, the absolute value of the implicit derivative is interpreted as the marginal rate of substitution
Marginal rate of substitution
In economics, the marginal rate of substitution is the rate at which a consumer is ready to give up one good in exchange for another good while maintaining the same level of utility.-Marginal rate of substitution as the slope of indifference curve:...
of the two goods: how much more of y one must receive in order to be indifferent to a loss of 1 unit of x.
See also
- Level setLevel setIn mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
- Isocontour
- IsosurfaceIsosurfaceAn isosurface is a three-dimensional analog of an isoline. It is a surface that represents points of a constant value within a volume of space; in other words, it is a level set of a continuous function whose domain is 3D-space.Isosurfaces are normally displayed using computer graphics, and are...
- Marginal rate of substitutionMarginal rate of substitutionIn economics, the marginal rate of substitution is the rate at which a consumer is ready to give up one good in exchange for another good while maintaining the same level of utility.-Marginal rate of substitution as the slope of indifference curve:...
- Implicit function theoremImplicit function theoremIn multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
- Logarithmic differentiation
- IterationIterationIteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
(Iterative solutions for implicit functions)

