
Maximal ideal
Encyclopedia
In mathematics
, more specifically in ring theory
, a maximal ideal is an ideal
which is maximal
(with respect to set inclusion) amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R. So there are no ideals "in between" I and R.
Maximal ideals are important because the quotient ring
s of maximal ideals are simple ring
s, and in the special case of unital commutative ring
s they are also field
s.
In noncommutative ring theory, a maximal right ideal is defined analogously as being a maximal in the poset of right ideals, and similarly, a maximal left ideal is defined. Since a one sided maximal ideal A is not necessarily twosided, the quotient R/A is not necessarily a ring, but it is a simple module
over R. If R has a unique maximal right ideal, then R is known as a local ring
, and the maximal right ideal is also the unique maximal left and unique maximal twosided ideal of the ring, and is in fact the Jacobson radical
J(R).
It is possible for a ring to have a unique maximal ideal and yet lack unique maximal one sided ideals: for example, in the ring of 2 by 2 square matrices over a field, the zero ideal is a maximal ideal, but there are many maximal right ideals.
Equivalently, I is a maximal ideal of R if I ≠ R and for all ideals J with I ⊆ J, either J = I or J = R.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a maximal ideal is an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
which is maximal
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
(with respect to set inclusion) amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R. So there are no ideals "in between" I and R.
Maximal ideals are important because the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
s of maximal ideals are simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
s, and in the special case of unital commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s they are also field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s.
In noncommutative ring theory, a maximal right ideal is defined analogously as being a maximal in the poset of right ideals, and similarly, a maximal left ideal is defined. Since a one sided maximal ideal A is not necessarily twosided, the quotient R/A is not necessarily a ring, but it is a simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
over R. If R has a unique maximal right ideal, then R is known as a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, and the maximal right ideal is also the unique maximal left and unique maximal twosided ideal of the ring, and is in fact the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
J(R).
It is possible for a ring to have a unique maximal ideal and yet lack unique maximal one sided ideals: for example, in the ring of 2 by 2 square matrices over a field, the zero ideal is a maximal ideal, but there are many maximal right ideals.
Definition
Given a ring R and a proper ideal I of R (that is I ≠ R), I is called a maximal ideal of R if there exists no other proper ideal J of R so that I ⊂ J.Equivalently, I is a maximal ideal of R if I ≠ R and for all ideals J with I ⊆ J, either J = I or J = R.
Examples
- In the ring Z of integers the maximal ideals are the principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
s generated by a prime number. - More generally, all nonzero prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s are maximal in a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
. - The maximal ideals of the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over an algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
K are the ideal of the form . This result is known as the weak nullstellensatz.
Properties
- If R is a unital commutative ring with an ideal m, then k = R/m is a field if and only if m is a maximal ideal. In that case, R/m is known as the residue fieldResidue fieldIn mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
. This fact can fail in non-unital rings. For example, is a maximal ideal in
is a maximal ideal in  , but
, but 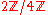 is not a field.
is not a field.
- If L is a maximal left ideal, then R/L is a simple left R module. Conversely in rings with unity, any simple left R module arises this way. Incidentally this shows that a collection of representatives of simple left R modules is actually a set since it can be put into correspondence with part of the set of maximal left ideals of R.
- Krull's theoremKrull's theoremIn mathematics, more specifically in ring theory, Krull's theorem, named after Wolfgang Krull, proves the existence of maximal ideals in any unital ring. The theorem was first stated in 1929 and is equivalent to the axiom of choice.- Krull's theorem :...
(1929): Every ring with a multiplicative identity has a maximal ideal. The result is also true if "ideal" is replaced with "right ideal" or "left ideal". More generally, it is true that every nonzero finitely generated module has a maximal submodule. Suppose I is an ideal which is not R (respectively, A is a right ideal which is not R). Then R/I is a ring with unity, (respectively, R/A is a finitely generated module), and so the above theorems can be applied to the quotient to conclude that there is a maximal ideal (respectively maximal right ideal) of R containing I (respectively, A).
- Krull's theorem can fail for rings without unity. A radical ring, i.e. a ring in which the Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
is the entire ring, has no simple modules and hence has no maximal right or left ideals.
- In a commutative ring with unity, every maximal ideal is a prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
. The converse is not always true: for example, in any nonfield integral domain the zero ideal is a prime ideal which is not maximal. Commutative rings in which prime ideals are maximal are known as zero-dimensional rings, where the dimension used is the Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
.

