
Christoffel symbols
Encyclopedia
In mathematics
and physics
, the Christoffel symbols, named for Elwin Bruno Christoffel
(1829–1900), are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport
in curved surface
s and, more generally, manifold
s. As such, they are coordinate-space expressions for the Levi-Civita connection
derived from the metric tensor
. In a broader sense, the connection coefficients of an arbitrary (not necessarily metric) affine connection
in a coordinate basis are also called Christoffel symbols. The Christoffel symbols may be used for performing practical calculations in differential geometry. For example, the Riemann curvature tensor
can be expressed entirely in terms of the Christoffel symbols and their first partial derivative
s.
At each point of the underlying n-dimensional manifold, for any local coordinate system, the Christoffel symbol is an array
with three dimensions: n × n × n. Each of the n3 components is a real number
.
Under linear coordinate transformations on the manifold, it behaves like a tensor
, but under general coordinate transformations, it does not. In many practical problems, most components of the Christoffel symbols are equal to zero
, provided the coordinate system and the metric tensor possess some common symmetries.
In general relativity, the Christoffel symbol plays the role of the gravitational force field with the corresponding gravitational potential being the metric tensor.
s and pseudo-Riemannian manifold
s, such as those of general relativity
, with careful distinction being made between upper and lower indices (contra-variant and co-variant indices). The formulas hold for either sign convention
, unless otherwise noted.
Einstein summation convention
is used in this article.
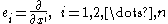
define a basis of the tangent space of M at each point.

 (sometimes Γkij ) are defined as the unique coefficients such that the equation
(sometimes Γkij ) are defined as the unique coefficients such that the equation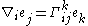
holds, where is the Levi-Civita connection on M taken in the coordinate direction ei.
is the Levi-Civita connection on M taken in the coordinate direction ei.
The Christoffel symbols can be derived from the vanishing of the covariant derivative
of the metric tensor
 :
:
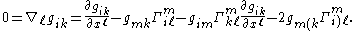
As a shorthand notation, the nabla symbol
and the partial derivative symbols are frequently dropped, and instead a semi-colon and a comma are used to set off the index that is being used for the derivative. Thus, the above is sometimes written as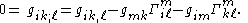
By permuting the indices, and resumming, one can solve explicitly for the Christoffel symbols as a function of the metric tensor: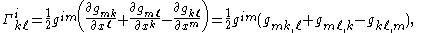
where the matrix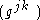 is an inverse of the matrix
is an inverse of the matrix 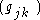 , defined as (using the Kronecker delta, and Einstein notation
, defined as (using the Kronecker delta, and Einstein notation
for summation)
 .
.
Although the Christoffel symbols are written in the same notation as tensors with index notation, they are not tensor
s,
since they do not transform like tensors under a change of coordinates; see below.
The Christoffel symbols are most typically defined in a coordinate basis, which is the convention followed here. However, the Christoffel symbols can also be defined in an arbitrary basis of tangent vectors ei by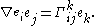
Explicitly, in terms of the metric tensor, this is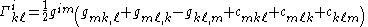
where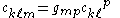 are the commutation coefficients of the basis; that is,
are the commutation coefficients of the basis; that is,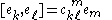
where ek are the basis vector
s and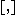 is the Lie bracket
is the Lie bracket
. The standard unit vectors in spherical and cylindrical coordinates
furnish an example of a basis with non-vanishing commutation coefficients.
The expressions below are valid only in a coordinate basis, unless otherwise noted.
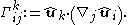
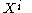 and
and  . Then the kth component of the covariant derivative of Y with respect to X is given by
. Then the kth component of the covariant derivative of Y with respect to X is given by
Here, the Einstein notation
is used, so repeated indices indicate summation over indices and contraction with the metric tensor serves to raise and lower indices: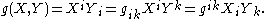
Keep in mind that and that
and that  , the Kronecker delta. The convention is that the metric tensor is the one with the lower indices; the correct way to obtain
, the Kronecker delta. The convention is that the metric tensor is the one with the lower indices; the correct way to obtain 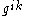 from
from 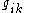 is to solve the linear equations
is to solve the linear equations 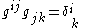 .
.
The statement that the connection is torsion
-free, namely that
is equivalent to the statement that the Christoffel symbol is symmetric in the lower two indices: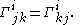
The index-less transformation properties of a tensor are given by pullbacks for covariant indices, and pushforwards for contravariant indices. The article on covariant derivatives provides additional discussion of the correspondence between index-free and indexed notation.
of a vector field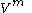 is
is
The covariant derivative of a scalar field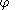 is just
is just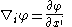
and the covariant derivative of a covector field is
is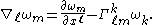
The symmetry of the Christoffel symbol now implies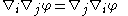
for any scalar field, but in general the covariant derivatives of higher order tensor fields do not commute (see curvature tensor
).
The covariant derivative of a type (2,0) tensor
field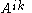 is
is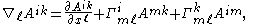
that is,
If the tensor field is mixed
then its covariant derivative is
and if the tensor field is of type (0,2) then its covariant derivative is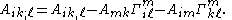
 to
to  , vectors transform as
, vectors transform as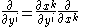
and so
where the overline denotes the Christoffel symbols in the y coordinate system. Note that the Christoffel symbol does not transform as a tensor, but rather as an object in the jet bundle
.
In fact, at each point, there exist coordinate systems in which the Christoffel symbols vanish at the point. These are called (geodesic) normal coordinates
, and are often used in Riemannian geometry
.
, where spacetime
is represented by a curved 4-dimensional Lorentz manifold with a Levi-Civita connection
. The Einstein field equations
—which determine the geometry of spacetime in the presence of matter—contain the Ricci tensor, and so calculating the Christoffel symbols is essential. Once the geometry is determined, the paths of particles and light beams are calculated by solving the geodesic equations
in which the Christoffel symbols explicitly appear.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Christoffel symbols, named for Elwin Bruno Christoffel
Elwin Bruno Christoffel
Elwin Bruno Christoffel was a German mathematician and physicist.-Life:...
(1829–1900), are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
in curved surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s and, more generally, manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. As such, they are coordinate-space expressions for the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
derived from the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. In a broader sense, the connection coefficients of an arbitrary (not necessarily metric) affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
in a coordinate basis are also called Christoffel symbols. The Christoffel symbols may be used for performing practical calculations in differential geometry. For example, the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
can be expressed entirely in terms of the Christoffel symbols and their first partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s.
At each point of the underlying n-dimensional manifold, for any local coordinate system, the Christoffel symbol is an array
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with three dimensions: n × n × n. Each of the n3 components is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
Under linear coordinate transformations on the manifold, it behaves like a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, but under general coordinate transformations, it does not. In many practical problems, most components of the Christoffel symbols are equal to zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, provided the coordinate system and the metric tensor possess some common symmetries.
In general relativity, the Christoffel symbol plays the role of the gravitational force field with the corresponding gravitational potential being the metric tensor.
Preliminaries
The definitions given below are valid for both Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s and pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s, such as those of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, with careful distinction being made between upper and lower indices (contra-variant and co-variant indices). The formulas hold for either sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
, unless otherwise noted.
Einstein summation convention
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
is used in this article.
Definition
If xi, i = 1,2,...,n, is a local coordinate system on a manifold M, then the tangent vectorsTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
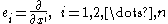
define a basis of the tangent space of M at each point.
Christoffel symbols of the first kind
The Christoffel symbols of the first kind can be derived from the Christoffel symbols of the second kind and the metric,
Christoffel symbols of the second kind (symmetric definition)
The Christoffel symbols of the second kind, using the definition symmetric in i and j, (sometimes Γkij ) are defined as the unique coefficients such that the equation
(sometimes Γkij ) are defined as the unique coefficients such that the equation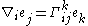
holds, where
 is the Levi-Civita connection on M taken in the coordinate direction ei.
is the Levi-Civita connection on M taken in the coordinate direction ei.The Christoffel symbols can be derived from the vanishing of the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
 :
: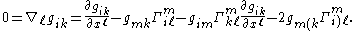
As a shorthand notation, the nabla symbol
Nabla symbol
right|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...
and the partial derivative symbols are frequently dropped, and instead a semi-colon and a comma are used to set off the index that is being used for the derivative. Thus, the above is sometimes written as
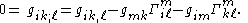
By permuting the indices, and resumming, one can solve explicitly for the Christoffel symbols as a function of the metric tensor:
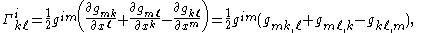
where the matrix
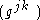 is an inverse of the matrix
is an inverse of the matrix 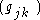 , defined as (using the Kronecker delta, and Einstein notation
, defined as (using the Kronecker delta, and Einstein notationEinstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
for summation)
 .
.Although the Christoffel symbols are written in the same notation as tensors with index notation, they are not tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s,
since they do not transform like tensors under a change of coordinates; see below.
The Christoffel symbols are most typically defined in a coordinate basis, which is the convention followed here. However, the Christoffel symbols can also be defined in an arbitrary basis of tangent vectors ei by
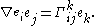
Explicitly, in terms of the metric tensor, this is
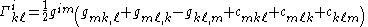
where
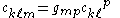 are the commutation coefficients of the basis; that is,
are the commutation coefficients of the basis; that is,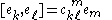
where ek are the basis vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and
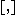 is the Lie bracket
is the Lie bracketLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
. The standard unit vectors in spherical and cylindrical coordinates
Vector fields in cylindrical and spherical coordinates
* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in question. \phi is the angle between the projection of the radius vector onto the x-y plane and the x axis...
furnish an example of a basis with non-vanishing commutation coefficients.
The expressions below are valid only in a coordinate basis, unless otherwise noted.
Christoffel symbols of the second kind (asymmetric definition)
A different definition of Christoffel symbols of the second kind is Misner et al.'s 1973 definition, which is asymmetric in i and j: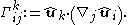
Relationship to index-free notation
Let X and Y be vector fields with components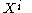 and
and  . Then the kth component of the covariant derivative of Y with respect to X is given by
. Then the kth component of the covariant derivative of Y with respect to X is given by
Here, the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
is used, so repeated indices indicate summation over indices and contraction with the metric tensor serves to raise and lower indices:
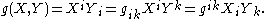
Keep in mind that
 and that
and that  , the Kronecker delta. The convention is that the metric tensor is the one with the lower indices; the correct way to obtain
, the Kronecker delta. The convention is that the metric tensor is the one with the lower indices; the correct way to obtain 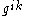 from
from 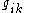 is to solve the linear equations
is to solve the linear equations 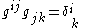 .
.The statement that the connection is torsion
Torsion
The word torsion may refer to the following:*In geometry:** Torsion of a curve** Torsion tensor in differential geometry** The closely related concepts of Reidemeister torsion and analytic torsion ** Whitehead torsion*In algebra:** Torsion ** Tor functor* In medicine:** Ovarian...
-free, namely that

is equivalent to the statement that the Christoffel symbol is symmetric in the lower two indices:
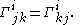
The index-less transformation properties of a tensor are given by pullbacks for covariant indices, and pushforwards for contravariant indices. The article on covariant derivatives provides additional discussion of the correspondence between index-free and indexed notation.
Covariant derivatives of tensors
The covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of a vector field
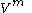 is
is
The covariant derivative of a scalar field
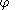 is just
is just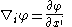
and the covariant derivative of a covector field
 is
is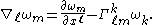
The symmetry of the Christoffel symbol now implies
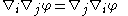
for any scalar field, but in general the covariant derivatives of higher order tensor fields do not commute (see curvature tensor
Curvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
).
The covariant derivative of a type (2,0) tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
field
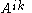 is
is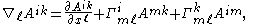
that is,

If the tensor field is mixed
Mixed tensor
In tensor analysis, a mixed tensor is a tensor which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed tensor will be a subscript and at least one of the indices will be a superscript ....
then its covariant derivative is

and if the tensor field is of type (0,2) then its covariant derivative is
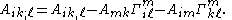
Change of variable
Under a change of variable from to
to  , vectors transform as
, vectors transform as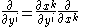
and so

where the overline denotes the Christoffel symbols in the y coordinate system. Note that the Christoffel symbol does not transform as a tensor, but rather as an object in the jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
.
In fact, at each point, there exist coordinate systems in which the Christoffel symbols vanish at the point. These are called (geodesic) normal coordinates
Normal coordinates
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p...
, and are often used in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
.
Applications to general relativity
The Christoffel symbols find frequent use in Einstein's theory of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, where spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is represented by a curved 4-dimensional Lorentz manifold with a Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
. The Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
—which determine the geometry of spacetime in the presence of matter—contain the Ricci tensor, and so calculating the Christoffel symbols is essential. Once the geometry is determined, the paths of particles and light beams are calculated by solving the geodesic equations
Solving the geodesic equations
Solving the geodesic equations is a procedure used in mathematics, particularly Riemannian geometry, and in physics, particularly in general relativity, that results in obtaining geodesics. Physically, these represent the paths of particles with no proper acceleration, their motion satisfying the...
in which the Christoffel symbols explicitly appear.
See also
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Proofs involving Christoffel symbols
- Differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
- List of formulas in Riemannian geometry
- Riemann–Christoffel tensor
- Gauss–Codazzi equationsGauss–Codazzi equationsIn Riemannian geometry, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurfaces in a Euclidean space, and more generally submanifolds of Riemannian manifolds...

