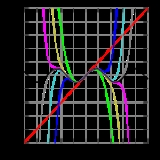
Taylor series
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Taylor series is a representation of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
as an infinite sum
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of terms that are calculated from the values of the function's derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s at a single point.
The concept of a Taylor series was formally introduced by the English mathematician Brook Taylor
Brook Taylor
Brook Taylor FRS was an English mathematician who is best known for Taylor's theorem and the Taylor series.- Life and work :...
in 1715. If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
, who made extensive use of this special case of Taylor series in the 18th century.
It is common practice to approximate a function by using a finite number of terms of its Taylor series.

