Exterior algebra

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

 to study area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

s, volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

s, and their higher-dimensional analogs. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector

Bivector

In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...

 and lives in a space called the exterior square, a geometrical space (vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

) that differs from the original space of vectors. The magnitude

Magnitude (mathematics)

The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....

 of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three-dimensions can also be computed using the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

 of the two vectors. Also like the cross product, the exterior product is anticommutative

Anticommutativity

In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...

, meaning that u ∧ v = −v ∧ u for all vectors u and v. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation

Orientation (mathematics)

In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...

 of their boundaries (a decision of clockwise or counterclockwise). When thought of in this manner (common in geometric algebra

Geometric algebra

Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...

) the exterior product of two vectors is called a 2-blade. More generally, the exterior product of any number k of vectors can be defined and is sometimes called a k-blade. It lives in a geometrical space known as the k-th exterior power. The magnitude of the resulting k-blade is the volume of the k-dimensional parallelotope whose sides are the given vectors, just like the magnitude of the scalar triple product of vectors in three dimensions gives the volume of the parallelepiped spanned by those vectors.

The exterior algebra (also known as the Grassmann algebra, after Hermann Grassmann

Hermann Grassmann

Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...

) is the algebraic system whose product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, whereas blades have a concrete geometrical interpretation, objects in the exterior algebra can be manipulated according to a set of unambiguous rules. The exterior algebra contains objects that are not just k-blades, but sums of k-blades; such a sum is called a k-vector. The k-blades, because they are simple products of vectors, are called the simple elements of the algebra. The rank of any element of the exterior algebra is defined to be the smallest number of simple elements of which it is a sum. An example when k = 2 is a symplectic form, which is an element of the exterior square whose rank is maximal. The exterior product extends to the full exterior algebra, so that it makes sense to multiply any two elements of the algebra. Equipped with this product, the exterior algebra is an associative algebra

Associative algebra

In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

, which means that for any elements α, β, γ. The k-vectors have degree k, meaning that they sums of products of k vectors, and elements of different degrees are multiplied, the degrees add (like multiplication of polynomials). This means that the exterior algebra is a graded algebra

Graded algebra

In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....

.

In a precise sense (given by what is known as a universal construction

Universal property

In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...

), the exterior algebra is the largest algebra that supports an alternating product on vectors, and can be easily defined in terms of other known objects such as tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

s. The definition of the exterior algebra makes sense for spaces not just of geometric vectors, but of other vector-like objects such as vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s or functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

. In full generality, the exterior algebra can be defined for modules

Module (mathematics)

In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...

 over a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

, and for other structures of interest in abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

. It is one of these more general constructions where the exterior algebra finds one of its most important applications, where it appears as the algebra of differential forms that is fundamental in areas that use differential geometry. Differential forms are mathematical objects that represent infinitesimal areas of infinitesimal parallelograms (and higher-dimensional bodies), and so can be integrated

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

 over surfaces and higher dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s in a way that generalizes the line integral

Line integral

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...

s from calculus. The exterior algebra also has many algebraic properties that make it a convenient tool in algebra itself. The association of the exterior algebra to a vector space is a type of functor

Functor

In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....

 on vector spaces, which means that it is compatible in a certain way with linear transformations of vector spaces. The exterior algebra is one example of a bialgebra

Bialgebra

In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....

, meaning that its dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

 also possesses a product, and this dual product is compatible with the wedge product. This dual algebra is precisely the algebra of alternating multilinear forms on V, and the pairing between the exterior algebra and its dual is given by the interior product.

Areas in the plane

The Cartesian plane R² is a vector space equipped with a basis consisting of a pair of unit vectors


Suppose that


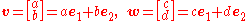
are a pair of given vectors in R², written in components. There is a unique parallelogram having v and w as two of its sides. The area of this parallelogram is given by the standard determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 formula:


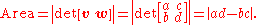
Consider now the exterior product of v and w:


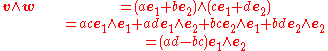
where the first step uses the distributive law for the wedge product, and the last uses the fact that the wedge product is alternating, and in particular e₂ ∧ e₁ = −e₁ ∧ e₂. Note that the coefficient in this last expression is precisely the determinant of the matrix [v w]. The fact that this may be positive or negative has the intuitive meaning that v and w may be oriented in a counterclockwise or clockwise sense as the vertices of the parallelogram they define. Such an area is called the signed area of the parallelogram: the absolute value of the signed area is the ordinary area, and the sign determines its orientation.

The fact that this coefficient is the signed area is not an accident. In fact, it is relatively easy to see that the exterior product should be related to the signed area if one tries to axiomatize this area as an algebraic construct. In detail, if A(v, w) denotes the signed area of the parallelogram determined by the pair of vectors v and w, then A must satisfy the following properties:

1. A(jv, kw) = j k A(v, w) for any real numbers j and k, since rescaling either of the sides rescales the area by the same amount (and reversing the direction of one of the sides reverses the orientation of the parallelogram).
2. A(v,v) = 0, since the area of the degenerate parallelogram determined by v (i.e., a line segment
   Line segment
   In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
   
   ) is zero.
3. A(w,v) = −A(v,w), since interchanging the roles of v and w reverses the orientation of the parallelogram.
4. A(v + jw,w) = A(v,w), since adding a multiple of w to v affects neither the base nor the height of the parallelogram and consequently preserves its area.
5. A(e₁, e₂) = 1, since the area of the unit square is one.

With the exception of the last property, the wedge product satisfies the same formal properties as the area. In a certain sense, the wedge product generalizes the final property by allowing the area of a parallelogram to be compared to that of any "standard" chosen parallelogram (here, the one with sides e₁ and e₂). In other words, the exterior product in two-dimensions provides a basis-independent formulation of area.

Cross and triple products

For vectors in R³, the exterior algebra is closely related to the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

 and triple product

Triple product

In mathematics, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product....

. Using the standard basis {e₁, e₂, e₃}, the wedge product of a pair of vectors


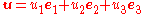
and


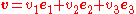
is


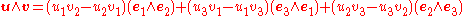
where {e₁ Λ e₂, e₃ Λ e₁, e₂ Λ e₃} is the basis for the three-dimensional space Λ²(R³). This imitates the usual definition of the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

 of vectors in three dimensions.

Bringing in a third vector


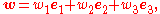
the wedge product of three vectors is


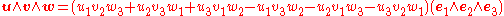
where e₁ Λ e₂ Λ e₃ is the basis vector for the one-dimensional space Λ³(R³). This imitates the usual definition of the triple product

Triple product

In mathematics, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product....

.

The cross product and triple product in three dimensions each admit both geometric and algebraic interpretations. The cross product u×v can be interpreted as a vector which is perpendicular to both u and v and whose magnitude is equal to the area of the parallelogram determined by the two vectors. It can also be interpreted as the vector consisting of the minors of the matrix with columns u and v. The triple product of u, v, and w is geometrically a (signed) volume. Algebraically, it is the determinant of the matrix with columns u, v, and w. The exterior product in three-dimensions allows for similar interpretations. In fact, in the presence of a positively oriented orthonormal basis

Orthonormal basis

In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

, the exterior product generalizes these notions to higher dimensions.

Formal definitions and algebraic properties

The exterior algebra Λ(V) over a vector space V over a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 K is defined as the quotient algebra

Quotient ring

In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...

 of the tensor algebra

Tensor algebra

In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...

 by the two-sided ideal

Ideal (ring theory)

In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....

 I generated by all elements of the form x ⊗ x such that x ∈ V. Symbolically,


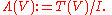
The wedge product ∧ of two elements of Λ(V) is defined by

Anticommutativity of the wedge product

The wedge product is alternating on elements of V, which means that x ∧ x = 0 for all x ∈ V. It follows that the product is also anticommutative on elements of V, for supposing that x, y ∈ V,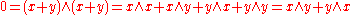


hence


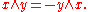
Conversely, it follows from the anticommutativity of the product that the product is alternating, unless K has characteristic two.

More generally, if x₁, x₂, ..., x_k are elements of V, and σ is a permutation

Permutation group

In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...

 of the integers [1,...,k], then


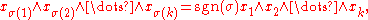
where sgn(σ) is the signature of the permutation σ.

The exterior power

The kth exterior power of V, denoted Λ^k(V), is the vector subspace of Λ(V) spanned

Linear span

In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...

 by elements of the form

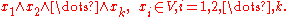
If α ∈ Λ^k(V), then α is said to be a k-multivector

Multivector

In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...

. If, furthermore, α can be expressed as a wedge product of k elements of V, then α is said to be decomposable. Although decomposable multivectors span Λ^k(V), not every element of Λ^k(V) is decomposable. For example, in R⁴, the following 2-multivector is not decomposable:
(This is in fact a symplectic form, since α ∧ α ≠ 0.)

Basis and dimension

If the dimension of V is n and {e₁,...,e_n} is a basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

 of V, then the set
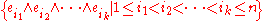
is a basis for Λ^k(V). The reason is the following: given any wedge product of the form
then every vector v_j can be written as a linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

 of the basis vectors e_i; using the bilinearity of the wedge product, this can be expanded to a linear combination of wedge products of those basis vectors. Any wedge product in which the same basis vector appears more than once is zero; any wedge product in which the basis vectors do not appear in the proper order can be reordered, changing the sign whenever two basis vectors change places. In general, the resulting coefficients of the basis k-vectors can be computed as the minor

Minor (linear algebra)

In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...

s of the matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 that describes the vectors v_j in terms of the basis e_i.

By counting the basis elements, the dimension of Λ^k(V) is equal to a binomial coefficient

Binomial coefficient

In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

:
In particular, Λ^k(V) = {0} for k > n.

Any element of the exterior algebra can be written as a sum of multivector

Multivector

In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...

s. Hence, as a vector space the exterior algebra is a direct sum

Direct sum of modules

In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...

(where by convention Λ⁰(V) = K and Λ¹(V) = V), and therefore its dimension is equal to the sum of the binomial coefficients, which is 2ⁿ.

Rank of a multivector

If α ∈ Λ^k(V), then it is possible to express α as a linear combination of decomposable multivector

Multivector

In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...

s:


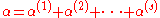
where each α⁽ⁱ⁾ is decomposable, say


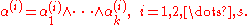
The rank of the multivector α is the minimal number of decomposable multivectors in such an expansion of α. This is similar to the notion of tensor rank.

Rank is particularly important in the study of 2-multivectors . The rank of a 2-multivector α can be identified with half the rank of the matrix of coefficients of α in a basis. Thus if e_i is a basis for V, then α can be expressed uniquely as


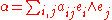
where a_ij = −a_ji (the matrix of coefficients is skew-symmetric). The rank of the matrix a_ij is therefore even, and is twice the rank of the form α.

In characteristic 0, the 2-multivector α has rank p if and only if


and

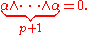
Graded structure

The wedge product of a k-multivector with a p-multivector is a (k+p)-multivector, once again invoking bilinearity. As a consequence, the direct sum decomposition of the preceding section


gives the exterior algebra the additional structure of a graded algebra

Graded algebra

In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....

. Symbolically,


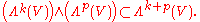
Moreover, the wedge product is graded anticommutative, meaning that if α ∈ Λ^k(V) and β ∈ Λ^p(V), then


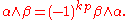
In addition to studying the graded structure on the exterior algebra, studies additional graded structures on exterior algebras, such as those on the exterior algebra of a graded module (a module that already carries its own gradation).

Universal property

Let V be a vector space over the field K. Informally, multiplication in Λ(V) is performed by manipulating symbols and imposing a distributive law, an associative law, and using the identity v ∧ v = 0 for v ∈ V. Formally, Λ(V) is the "most general" algebra in which these rules hold for the multiplication, in the sense that any unital associative K-algebra containing V with alternating multiplication on V must contain a homomorphic image of Λ(V). In other words, the exterior algebra has the following universal property

Universal property

In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...

:
To construct the most general algebra that contains V and whose multiplication is alternating on V, it is natural to start with the most general algebra that contains V, the tensor algebra

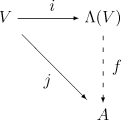
Tensor algebra

In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...

 T(V), and then enforce the alternating property by taking a suitable quotient

Quotient ring

In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...

. We thus take the two-sided ideal

Ideal (ring theory)

In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....

 I in T(V) generated by all elements of the form v⊗v for v in V, and define Λ(V) as the quotient


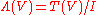
(and use Λ as the symbol for multiplication in Λ(V)). It is then straightforward to show that Λ(V) contains V and satisfies the above universal property.

As a consequence of this construction, the operation of assigning to a vector space V its exterior algebra Λ(V) is a functor

Functor

In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....

 from the category

Category (mathematics)

In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...

 of vector spaces to the category of algebras.

Rather than defining Λ(V) first and then identifying the exterior powers Λ^k(V) as certain subspaces, one may alternatively define the spaces Λ^k(V) first and then combine them to form the algebra Λ(V). This approach is often used in differential geometry and is described in the next section.

Generalizations

Given a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

 R and an R-module

Module (mathematics)

In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...

 M, we can define the exterior algebra Λ(M) just as above, as a suitable quotient of the tensor algebra T(M). It will satisfy the analogous universal property. Many of the properties of Λ(M) also require that M be a projective module

Projective module

In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...

. Where finite-dimensionality is used, the properties further require that M be finitely generated and projective. Generalizations to the most common situations can be found in .

Exterior algebras of vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

s are frequently considered in geometry and topology. There are no essential differences between the algebraic properties of the exterior algebra of finite-dimensional vector bundles and those of the exterior algebra of finitely-generated projective modules, by the Serre-Swan theorem. More general exterior algebras can be defined for sheaves

Sheaf (mathematics)

In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...

 of modules.

Alternating operators

Given two vector spaces V and X, an alternating operator (or anti-symmetric operator) from V^k to X is a multilinear map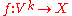


such that whenever v₁,...,v_k are linearly dependent vectors in V, then


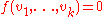
A well-known example is the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

, an alternating operator from (Kⁿ)ⁿ to K.

The map


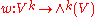
which associates to k vectors from V their wedge product, i.e. their corresponding k-vector, is also alternating. In fact, this map is the "most general" alternating operator defined on V^k: given any other alternating operator f : V^k → X, there exists a unique linear map φ: Λ^k(V) → X with f = φ o w. This universal property

Universal property

In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...

 characterizes the space Λ^k(V) and can serve as its definition.

Alternating multilinear forms

The above discussion specializes to the case when X = K, the base field. In this case an alternating multilinear function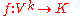
is called an alternating multilinear form. The set of all alternating multilinear forms is a vector space, as the sum of two such maps, or the product of such a map with a scalar, is again alternating. By the universal property of the exterior power, the space of alternating forms of degree k on V is naturally

Natural transformation

In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...

 isomorphic with the dual vector space (Λ^kV)^∗. If V is finite-dimensional, then the latter is naturally isomorphic to Λ^k(V^∗). In particular, the dimension of the space of anti-symmetric maps from V^k to K is the binomial coefficient

Binomial coefficient

In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

 n choose k.

Under this identification, the wedge product takes a concrete form: it produces a new anti-symmetric map from two given ones. Suppose ω : V^k → K and η : V^m → K are two anti-symmetric maps. As in the case of tensor product

Tensor product

In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...

s of multilinear maps, the number of variables of their wedge product is the sum of the numbers of their variables. It is defined as follows:


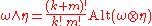
where the alternation Alt of a multilinear map is defined to be the signed average of the values over all the permutation

Permutation

In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

s of its variables:


This definition of the wedge product is well-defined even if the field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 K has finite characteristic, if
one considers an equivalent version of the above that does not use factorials or any constants:


where here Sh_k,m ⊂ S_k+m is the subset of (k,m) shuffles: permutation

Permutation

In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

s σ of the set {1,2,…,k+m} such that σ(1) < σ(2) < … < σ(k), and σ(k+1) < σ(k+2)< … <σ(k+m).

Bialgebra structure

In formal terms, there is a correspondence between the graded dual of the graded algebra Λ(V) and alternating multilinear forms on V. The wedge product of multilinear forms defined above is dual to a coproduct

Coproduct

In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...

 defined on Λ(V), giving the structure of a coalgebra

Coalgebra

In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...

.

The coproduct is a linear function Δ : Λ(V) → Λ(V) ⊗ Λ(V) given on decomposable elements by
For example,



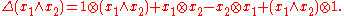
This extends by linearity to an operation defined on the whole exterior algebra. In terms of the coproduct, the wedge product on the dual space is just the graded dual of the coproduct:


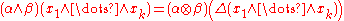
where the tensor product on the right-hand side is of multilinear linear maps (extended by zero on elements of incompatible homogeneous degree: more precisely, α∧β = ε o (α⊗β) o Δ, where ε is the counit, as defined presently).

The counit is the homomorphism ε : Λ(V) → K which returns the 0-graded component of its argument. The coproduct and counit, along with the wedge product, define the structure of a bialgebra

Bialgebra

In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....

 on the exterior algebra.

With an antipode defined on homogeneous elements by S(x) = (−1)^{deg x}x, the exterior algebra is furthermore a Hopf algebra

Hopf algebra

In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...

.

Interior product

Suppose that V is finite-dimensional. If V^* denotes the dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

 to the vector space V, then for each , it is possible to define an antiderivation

Derivation (abstract algebra)

In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...

 on the algebra Λ(V),


This derivation is called the interior product with α, or sometimes the insertion operator, or contraction by α.

Suppose that . Then w is a multilinear mapping of V^* to K, so it is defined by its values on the k-fold Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

 V^* × V^* × ... × V^*. If u₁, u₂, ..., u_k−1 are k−1 elements of V^*, then define


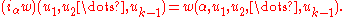
Additionally, let i_αf = 0 whenever f is a pure scalar (i.e., belonging to Λ⁰V).

Axiomatic characterization and properties

The interior product satisfies the following properties:

1. For each k and each α ∈ V^*,

   

   (By convention, Λ⁻¹ = {0}.)

2. If v is an element of V ( = Λ¹V), then i_αv = α(v) is the dual pairing between elements of V and elements of V^*.
3. For each α ∈ V^*, iα is a graded derivation of degree −1:

   

In fact, these three properties are sufficient to characterize the interior product as well as define it in the general infinite-dimensional case.

Further properties of the interior product include:

• 
• 

Hodge duality

Suppose that V has finite dimension n. Then the interior product induces a canonical isomorphism of vector spaces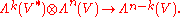
In the geometrical setting, a non-zero element of the top exterior power Λⁿ(V) (which is a one-dimensional vector space) is sometimes called a volume form

Volume form

In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...

 (or orientation form, although this term may sometimes lead to ambiguity.) Relative to a given volume form σ, the isomorphism is given explicitly by


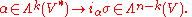
If, in addition to a volume form, the vector space V is equipped with an inner product identifying V with V^*, then the resulting isomorphism is called the Hodge dual (or more commonly the Hodge star operator)


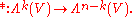
The composite of with itself maps Λ^k(V) → Λ^k(V) and is always a scalar multiple of the identity map. In most applications, the volume form is compatible with the inner product in the sense that it is a wedge product of an orthonormal basis

Orthonormal basis

In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

 of V. In this case,
where I is the identity, and the inner product has metric signature

Metric signature

The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...

 (p,q) — p plusses and q minuses.

Inner product

For V a finite-dimensional space, an inner product on V defines an isomorphism of V with V^∗, and so also an isomorphism of Λ^kV with (Λ^kV)^∗. The pairing between these two spaces also takes the form of an inner product. On decomposable k-multivectors,
the determinant of the matrix of inner products. In the special case v_i = w_i, the inner product is the square norm of the multivector, given by the determinant of the Gramian matrix (⟨v_i, v_j⟩). This is then extended bilinearly (or sesquilinearly in the complex case) to a non-degenerate inner product on Λ^kV. If e_i, i=1,2,...,n, form an orthonormal basis

Orthonormal basis

In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

 of V, then the vectors of the form
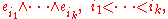
constitute an orthonormal basis for Λ^k(V).

With respect to the inner product, exterior multiplication and the interior product are mutually adjoint. Specifically, for v ∈ Λ^k−1(V), w ∈ Λ^k(V), and x ∈ V,
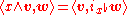
where x^♭ ∈ V^* is the linear functional defined by
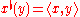
for all y ∈ V. This property completely characterizes the inner product on the exterior algebra.

Functoriality

Suppose that V and W are a pair of vector spaces and f : V → W is a linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

. Then, by the universal construction, there exists a unique homomorphism of graded algebras


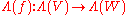
such that


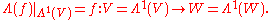
In particular, Λ(f) preserves homogeneous degree. The k-graded components of Λ(f) are given on decomposable elements by

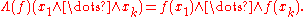
Let


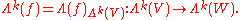
The components of the transformation Λ(k) relative to a basis of V and W is the matrix of k × k minors of f. In particular, if V = W and V is of finite dimension n, then Λⁿ(f) is a mapping of a one-dimensional vector space Λⁿ to itself, and is therefore given by a scalar: the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 of f.

Exactness

If


is a short exact sequence of vector spaces, then


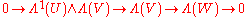
is an exact sequence of graded vector spaces as is

Direct sums

In particular, the exterior algebra of a direct sum is isomorphic to the tensor product of the exterior algebras: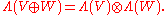


This is a graded isomorphism; i.e.,


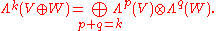
Slightly more generally, if


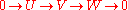
is a short exact sequence of vector spaces then Λ^k(V) has a filtration


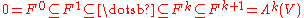
with quotients :. In particular, if U is 1-dimensional then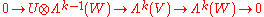


is exact, and if W is 1-dimensional then


is exact.

The alternating tensor algebra

If K is a field of characteristic 0, then the exterior algebra of a vector space V can be canonically identified with the vector subspace of T(V) consisting of antisymmetric tensors. Recall that the exterior algebra is the quotient of T(V) by the ideal I generated by x ⊗ x.

Let T^r(V) be the space of homogeneous tensors of degree r. This is spanned by decomposable tensors


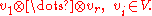
The antisymmetrization (or sometimes the skew-symmetrization) of a decomposable tensor is defined by


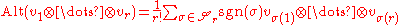
where the sum is taken over the symmetric group

Symmetric group

In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...

 of permutations on the symbols {1,...,r}. This extends by linearity and homogeneity to an operation, also denoted by Alt, on the full tensor algebra T(V). The image Alt(T(V)) is the alternating tensor algebra, denoted A(V). This is a vector subspace of T(V), and it inherits the structure of a graded vector space from that on T(V). It carries an associative graded product defined by


Although this product differs from the tensor product, the kernel of Alt is precisely the ideal I (again, assuming that K has characteristic 0), and there is a canonical isomorphism

Index notation

Suppose that V has finite dimension n, and that a basis e₁, ..., e_n of V is given. then any alternating tensor t ∈ A^r(V) ⊂ T^r(V) can be written in index notation

Index notation

Index notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...

 as


where t^{i₁ ... i_r} is completely antisymmetric in its indices.

The wedge product of two alternating tensors t and s of ranks r and p is given by


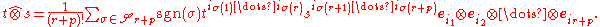
The components of this tensor are precisely the skew part of the components of the tensor product s ⊗ t, denoted by square brackets on the indices:

The interior product may also be described in index notation as follows. Let 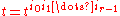be an antisymmetric tensor of rank r. Then, for α ∈ V^*, i_αt is an alternating tensor of rank r-1, given by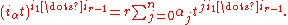


where n is the dimension of V.

Linear algebra

In applications to linear algebra

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

, the exterior product provides an abstract algebraic manner for describing the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 and the minors of a matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

. For instance, it is well-known that the magnitude of the determinant of a square matrix is equal to the volume of the parallelotope whose sides are the columns of the matrix. This suggests that the determinant can be defined in terms of the exterior product of the column vectors. Likewise, the k×k minors of a matrix can be defined by looking at the exterior products of column vectors chosen k at a time. These ideas can be extended not just to matrices but to linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

s as well: the magnitude of the determinant of a linear transformation is the factor by which it scales the volume of any given reference parallelotope. So the determinant of a linear transformation can be defined in terms of what the transformation does to the top exterior power. The action of a transformation on the lesser exterior powers gives a basis-independent way to talk about the minors of the transformation.

Linear geometry

The decomposable k-vectors have geometric interpretations: the bivector represents the plane spanned by the vectors, "weighted" with a number, given by the area of the oriented parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

 with sides u and v. Analogously, the 3-vector 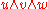represents the spanned 3-space weighted by the volume of the oriented parallelepiped

Parallelepiped

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...

 with edges u, v, and w.

Projective geometry

Decomposable k-vectors in Λ^kV correspond to weighted k-dimensional subspace

Subspace

-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...

s of V. In particular, the Grassmannian

Grassmannian

In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...

 of k-dimensional subspaces of V, denoted Gr_k(V), can be naturally identified with an algebraic subvariety

Algebraic variety

In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...

 of the projective space

Projective space

In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....

 P(Λ^kV). This is called the Plücker embedding

Plücker embedding

In mathematics, the Plücker embedding describes a method to realize the Grassmannian of all r-dimensional subspaces of a vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P....

.

Differential geometry

The exterior algebra has notable applications in differential geometry, where it is used to define differential form

Differential form

In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...

s. A differential form

Differential form

In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...

 at a point of a differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

 is an alternating multilinear form on the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

 at the point. Equivalently, a differential form of degree k is a linear functional

Linear functional

In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars.  In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...

 on the k-th exterior power of the tangent space. As a consequence, the wedge product of multilinear forms defines a natural wedge product for differential forms. Differential forms play a major role in diverse areas of differential geometry.

In particular, the exterior derivative

Exterior derivative

In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....

 gives the exterior algebra of differential forms on a manifold the structure of a differential algebra

Differential algebra

In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...

. The exterior derivative commutes with pullback along smooth mappings between manifolds, and it is therefore a natural

Natural transformation

In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...

 differential operator

Differential operator

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...

. The exterior algebra of differential forms, equipped with the exterior derivative, is a differential complex whose cohomology is called the de Rham cohomology

De Rham cohomology

In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...

 of the underlying manifold and plays a vital role in the algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

 of differentiable manifolds.

Representation theory

In representation theory

Representation theory

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

, the exterior algebra is one of the two fundamental Schur functor

Schur functor

In mathematics, especially in the field of representation theory, a Schur functor is a functor from the category of modules over a fixed commutative ring to itself. Schur functors are indexed by partitions and are described as follows. Let R be a commutative ring, E an R moduleand λ a partition of...

s on the category of vector spaces, the other being the symmetric algebra

Symmetric algebra

In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....

. Together, these constructions are used to generate the irreducible representations of the general linear group

General linear group

In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...

; see fundamental representation

Fundamental representation

In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...

.

Physics

The exterior algebra is an archetypal example of a superalgebra

Superalgebra

In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....

, which plays a fundamental role in physical theories pertaining to fermion

Fermion

In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....

s and supersymmetry

Supersymmetry

In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...

. For a physical discussion, see Grassmann number

Grassmann number

In mathematical physics, a Grassmann number, named after Hermann Grassmann, is a mathematical construction which allows a path integral representation for Fermionic fields...

. For various other applications of related ideas to physics, see superspace

Superspace

"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....

 and supergroup (physics)

Supergroup (physics)

The concept of supergroup is a generalization of that of group. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them....

.

Lie algebra homology

Let L be a Lie algebra over a field k, then it is possible to define the structure of a chain complex

Chain complex

In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...

 on the exterior algebra of L. This is a k-linear mapping
defined on decomposable elements by
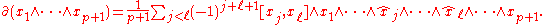
The Jacobi identity

Jacobi identity

In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...

 holds if and only if ∂∂ = 0, and so this is a necessary and sufficient condition for an anticommutative nonassociative algebra L to be a Lie algebra. Moreover, in that case ΛL is a chain complex

Chain complex

In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...

 with boundary operator ∂. The homology

Homology theory

In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...

 associated to this complex is the Lie algebra homology.

Homological algebra

The exterior algebra is the main ingredient in the construction of the Koszul complex

Koszul complex

In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...

, a fundamental object in homological algebra

Homological algebra

Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...

.

History

The exterior algebra was first introduced by Hermann Grassmann

Hermann Grassmann

Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...

 in 1844 under the blanket term of Ausdehnungslehre, or Theory of Extension.
This referred more generally to an algebraic (or axiomatic) theory of extended quantities and was one of the early precursors to the modern notion of a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

. Saint-Venant

Adhémar Jean Claude Barré de Saint-Venant

Adhémar Jean Claude Barré de Saint-Venant was a mechanician and mathematician who contributed to early stress analysis and also developed the one-dimensional unsteady open channel flow shallow water equations or Saint-Venant equations that are a fundamental set of equations used in modern...

 also published similar ideas of exterior calculus for which he claimed priority over Grassmann.

The algebra itself was built from a set of rules, or axioms, capturing the formal aspects of Cayley and Sylvester's theory of multivectors. It was thus a calculus, much like the propositional calculus

Propositional calculus

In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...

, except focused exclusively on the task of formal reasoning in geometrical terms.
In particular, this new development allowed for an axiomatic characterization of dimension, a property that had previously only been examined from the coordinate point of view.

The import of this new theory of vectors and multivector

Multivector

In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...

s was lost to mid 19th century mathematicians,
until being thoroughly vetted by Giuseppe Peano

Giuseppe Peano

Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...

 in 1888. Peano's work also remained somewhat obscure until the turn of the century, when the subject was unified by members of the French geometry school (notably Henri Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

, Élie Cartan

Élie Cartan

Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...

, and Gaston Darboux) who applied Grassmann's ideas to the calculus of differential form

Differential form

In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...

s.

A short while later, Alfred North Whitehead

Alfred North Whitehead

Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...

, borrowing from the ideas of Peano and Grassmann, introduced his universal algebra

Universal algebra

Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....

. This then paved the way for the 20th century developments of abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

 by placing the axiomatic notion of an algebraic system on a firm logical footing.

See also

• symmetric algebra
  Symmetric algebra
  In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
  
  , the symmetric analog
• Clifford algebra
  Clifford algebra
  In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
  
  , a quantum deformation
  Quantization (physics)
  In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
  
   of the exterior algebra by a quadratic form
  Quadratic form
  In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
  
  
• Weyl algebra, a quantum deformation of the symmetric algebra by a symplectic form
• multilinear algebra
  Multilinear algebra
  In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
  
  
• tensor algebra
  Tensor algebra
  In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
  
  
• geometric algebra
  Geometric algebra
  Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
  
  
• Koszul complex
  Koszul complex
  In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...
  
  

Mathematical references

Includes a treatment of alternating tensors and alternating forms, as well as a detailed discussion of Hodge duality from the perspective adopted in this article.

This is the main mathematical reference for the article. It introduces the exterior algebra of a module over a commutative ring (although this article specializes primarily to the case when the ring is a field), including a discussion of the universal property, functoriality, duality, and the bialgebra structure. See chapters III.7 and III.11.

This book contains applications of exterior algebras to problems in partial differential equations. Rank and related concepts are developed in the early chapters.

Chapter XVI sections 6-10 give a more elementary account of the exterior algebra, including duality, determinants and minors, and alternating forms.

Contains a classical treatment of the exterior algebra as alternating tensors, and applications to differential geometry.

Historical references

(The Linear Extension Theory - A new Branch of Mathematics) alternative reference; .

Other references and further reading

An introduction to the exterior algebra, and geometric algebra

Geometric algebra

Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...

, with a focus on applications. Also includes a history section and bibliography.

Includes applications of the exterior algebra to differential forms, specifically focused on integration

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

 and Stokes's theorem. The notation Λ^kV in this text is used to mean the space of alternating k-forms on V; i.e., for Spivak Λ^kV is what this article would call Λ^kV*. Spivak discusses this in Addendum 4.

Includes an elementary treatment of the axiomatization of determinants as signed areas, volumes, and higher-dimensional volumes.

• Wendell H. Fleming (1965) Functions of Several Variables, Addison-Wesley
  Addison-Wesley
  Addison-Wesley was a book publisher in Boston, Massachusetts, best known for its textbooks and computer literature. As well as publishing books, Addison-Wesley also distributed its technical titles through the Safari Books Online e-reference service...
  
  .

Chapter 6: Exterior algebra and differential calculus, pages 205-38. This textbook in multivariate calculus introduces the exterior algebra of differential forms adroitly into the calculus sequence for colleges.

An introduction to the coordinate-free approach in basic finite-dimensional linear algebra, using exterior products.