Cotangent bundle
Encyclopedia
In mathematics
, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle
of all the cotangent space
s at every point in the manifold. It may be described also as the dual bundle
to the tangent bundle
.
sections
of the cotangent bundle are differential one-form
s.
of M with itself. The diagonal mapping Δ sends a point p in M to the point (p,p) of M×M. The image of Δ is called the diagonal. Let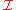
be the sheaf
of germs
of smooth functions on M×M which vanish on the diagonal. Then the quotient sheaf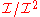
consists of equivalence classes of functions which vanish on the diagonal modulo higher order terms. The cotangent sheaf is the pullback
of this sheaf to M:
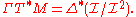
By Taylor's theorem
, this is a locally free sheaf of modules with respect to the sheaf of germs of smooth functions of M. Thus it defines a vector bundle
on M: the cotangent bundle.
, it can be regarded as a manifold in its own right. Because of the manner in which the definition of T*M relates to the differential topology
of the base space M, X possesses a canonical one-form θ (also tautological one-form
or symplectic potential). The exterior derivative
of θ is a symplectic 2-form, out of which a non-degenerate volume form
can be built for X. For example, as a result X is always an orientable manifold (meaning that the tangent bundle of X is an orientable vector bundle). A special set of coordinates can be defined on the cotangent bundle; these are called the canonical coordinates
. Because cotangent bundles can be thought of as symplectic manifold
s, any real function on the cotangent bundle can be interpreted to be a Hamiltonian
; thus the cotangent bundle can be understood to be a phase space
on which Hamiltonian mechanics
plays out.
of the vector bundle T*(T*M) over T*M.
This section can be constructed in several ways. The most elementary method is to use local coordinates. Suppose that xi are local coordinates on the base manifold M. In terms of these base coordinates, there are fibre coordinates pi: a one-form at a particular point of T*M has the form pidxi (Einstein summation convention implied). So the manifold T*M itself carries local coordinates (xi,pi) where the x are coordinates on the base and the p are coordinates in the fibre. The canonical one-form is given in these coordinates by
Intrinsically, the value of the canonical one-form in each fixed point of T*M is given as a pullback. Specifically, suppose that is the projection
of the bundle. Taking a point in Tx*M is the same as choosing of a point x in M and a one-form ω at x, and the tautological one-form θ assigns to the point (x, ω) the value
That is, for a vector v in the tangent bundle of the cotangent bundle, the application of the tautological one-form θ to v at (x, ω) is computed by projecting v into the tangent bundle at x using and applying ω to this projection. Note that the tautological one-form is not a pullback of a one-form on the base M.
of the canonical one-form
, the symplectic potential. Proving that this form is, indeed, symplectic can be done by noting that being symplectic is a local property: since the cotangent bundle is locally trivial, this definition need only be checked on
. But there the one form defined is the sum of 
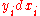, and the differential is the canonical symplectic form, the sum of 
.
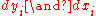represents the set of possible positions in a dynamical system
, then the cotangent bundle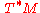
can be thought of as the set of possible positions and momenta. For example, this is a way to describe the phase space
of a pendulum. The state of the pendulum is determined by its position (an angle) and its momentum (or equivalently, its velocity, since its mass is not changing). The entire state space looks like a cylinder. The cylinder is the cotangent bundle of the circle. The above symplectic construction, along with an appropriate energy
function, gives a complete determination of the physics of system. See Hamiltonian mechanics
for more information, and the article on geodesic flow for an explicit construction of the Hamiltonian equations of motion.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
of all the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
s at every point in the manifold. It may be described also as the dual bundle
Dual bundle
In mathematics, the dual bundle of a vector bundle π : E → X is a vector bundle π* : E* → X whose fibers are the dual spaces to the fibers of E...
to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
.
The cotangent sheaf
SmoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
sections
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
of the cotangent bundle are differential one-form
One-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
s.
Definition of the cotangent sheaf
Let M×M be the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of M with itself. The diagonal mapping Δ sends a point p in M to the point (p,p) of M×M. The image of Δ is called the diagonal. Let
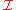be the sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of smooth functions on M×M which vanish on the diagonal. Then the quotient sheaf
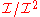consists of equivalence classes of functions which vanish on the diagonal modulo higher order terms. The cotangent sheaf is the pullbackInverse image functor
In mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
of this sheaf to M:
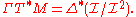
By Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
, this is a locally free sheaf of modules with respect to the sheaf of germs of smooth functions of M. Thus it defines a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
on M: the cotangent bundle.
The cotangent bundle as phase space
Since the cotangent bundle X=T*M is a vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, it can be regarded as a manifold in its own right. Because of the manner in which the definition of T*M relates to the differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
of the base space M, X possesses a canonical one-form θ (also tautological one-form
Tautological one-form
In mathematics, the tautological one-form is a special 1-form defined on the cotangent bundle T*Q of a manifold Q. The exterior derivative of this form defines a symplectic form giving T*Q the structure of a symplectic manifold. The tautological one-form plays an important role in relating the...
or symplectic potential). The exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of θ is a symplectic 2-form, out of which a non-degenerate volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
can be built for X. For example, as a result X is always an orientable manifold (meaning that the tangent bundle of X is an orientable vector bundle). A special set of coordinates can be defined on the cotangent bundle; these are called the canonical coordinates
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
. Because cotangent bundles can be thought of as symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s, any real function on the cotangent bundle can be interpreted to be a Hamiltonian
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
; thus the cotangent bundle can be understood to be a phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
on which Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
plays out.
The tautological one-form
The cotangent bundle carries a tautological one-form θ also known as the Poincaré 1-form or Liouville 1-form. (The form is also known as the canonical one-form, although this can sometimes lead to confusion.) This means that if we regard T*M as a manifold in its own right, there is a canonical sectionSection (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the vector bundle T*(T*M) over T*M.
This section can be constructed in several ways. The most elementary method is to use local coordinates. Suppose that xi are local coordinates on the base manifold M. In terms of these base coordinates, there are fibre coordinates pi: a one-form at a particular point of T*M has the form pidxi (Einstein summation convention implied). So the manifold T*M itself carries local coordinates (xi,pi) where the x are coordinates on the base and the p are coordinates in the fibre. The canonical one-form is given in these coordinates by
Intrinsically, the value of the canonical one-form in each fixed point of T*M is given as a pullback. Specifically, suppose that is the projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
of the bundle. Taking a point in Tx*M is the same as choosing of a point x in M and a one-form ω at x, and the tautological one-form θ assigns to the point (x, ω) the value
That is, for a vector v in the tangent bundle of the cotangent bundle, the application of the tautological one-form θ to v at (x, ω) is computed by projecting v into the tangent bundle at x using and applying ω to this projection. Note that the tautological one-form is not a pullback of a one-form on the base M.
Symplectic form
The cotangent bundle has a canonical symplectic 2-form on it, as an exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of the canonical one-form
Tautological one-form
In mathematics, the tautological one-form is a special 1-form defined on the cotangent bundle T*Q of a manifold Q. The exterior derivative of this form defines a symplectic form giving T*Q the structure of a symplectic manifold. The tautological one-form plays an important role in relating the...
, the symplectic potential. Proving that this form is, indeed, symplectic can be done by noting that being symplectic is a local property: since the cotangent bundle is locally trivial, this definition need only be checked on
. But there the one form defined is the sum of 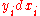, and the differential is the canonical symplectic form, the sum of 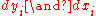.Phase space
If the manifold represents the set of possible positions in a dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, then the cotangent bundle
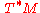can be thought of as the set of possible positions and momenta. For example, this is a way to describe the phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of a pendulum. The state of the pendulum is determined by its position (an angle) and its momentum (or equivalently, its velocity, since its mass is not changing). The entire state space looks like a cylinder. The cylinder is the cotangent bundle of the circle. The above symplectic construction, along with an appropriate energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
function, gives a complete determination of the physics of system. See Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
for more information, and the article on geodesic flow for an explicit construction of the Hamiltonian equations of motion.