In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a Lie algebra (icon, not ˈ) is an algebraic structure

Algebraic structure

In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...

 whose main use is in studying geometric objects such as Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s and differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

s. Lie algebras were introduced to study the concept of infinitesimal transformation

Infinitesimal transformation

In mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...

s. The term "Lie algebra" (after Sophus Lie

Sophus Lie

Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...

) was introduced by Hermann Weyl

Hermann Weyl

Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...

 in the 1930s. In older texts, the name "infinitesimal group" is used.
A Lie algebra is a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

  over some field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 F together with a binary operation

Binary operation

In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....

 [·, ·]

called the Lie bracket, which satisfies the following axioms:

• Bilinearity
  Bilinear operator
  In mathematics, a bilinear operator is a function combining elements of two vector spaces to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication is an example.-Definition:...
  
  :

for all scalars a, b in F and all elements x, y, z in .

• Alternating on :

for all x in .

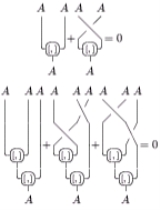
• The Jacobi identity
  Jacobi identity
  In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
  
  :

for all x, y, z in .

Note that the bilinearity and alternating properties imply anticommutativity

Anticommutativity

In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...

, i.e., for all elements x, y in , while anticommutativity only implies the alternating property if the field's characteristic

Characteristic (algebra)

In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...

 is not 2.

For any associative algebra

Associative algebra

In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

 A with multiplication , one can construct a Lie algebra L(A).