
Calculus
Encyclopedia
Calculus is a branch of mathematics
focused on limits
, functions
, derivative
s, integral
s, and infinite series
. This subject constitutes a major part of modern mathematics education
. It has two major branches, differential calculus
and integral calculus, which are related by the fundamental theorem of calculus
. Calculus is the study of change, in the same way that geometry
is the study of shape and algebra
is the study of operations and their application to solving equations. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study of functions and limits, broadly called mathematical analysis
. Calculus has widespread applications in science
, economics
, and engineering
and can solve many problems for which algebra
alone is insufficient.
Historically, calculus was called "the calculus of infinitesimal
s", or "infinitesimal calculus
". More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus
, variational calculus, lambda calculus
, pi calculus, and join calculus.
 The ancient period introduced some of the ideas that led to integral
The ancient period introduced some of the ideas that led to integral
calculus, but does not seem to have developed these ideas in a rigorous or systematic way. Calculations of volumes and areas, one goal of integral calculus, can be found in the Egyptian
Moscow papyrus
(c. 1820 BC), but the formulas are mere instructions, with no indication as to method, and some of them are wrong. From the age of Greek mathematics
, Eudoxus
(c. 408−355 BC) used the method of exhaustion
, which prefigures the concept of the limit, to calculate areas and volumes, while Archimedes
(c. 287−212 BC) developed this idea further
, inventing heuristics which resemble the methods of integral calculus. The method of exhaustion
was later reinvented in China
by Liu Hui
in the 3rd century AD in order to find the area of a circle. In the 5th century AD, Zu Chongzhi
established a method which would later be called Cavalieri's principle
to find the volume of a sphere
.
and the Kerala school of astronomy and mathematics stated many components of calculus such as the Taylor series
, infinite series approximations, an integral test for convergence
, early forms of differentiation, term by term integration, iterative methods for solutions of non-linear equations, and the theory that the area under a curve is its integral. Some consider the Yuktibhāṣā
to be the first text on calculus.
In Europe, the foundational work was a treatise due to Bonaventura Cavalieri
, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimally thin cross-sections. The ideas were similar to Archimedes' in The Method
, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods could lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first.
The formal study of calculus combined Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. Pierre de Fermat
, claiming that he borrowed from Diophantus
, introduced the concept of adequality
, which represented equality up to an infinitesimal error term. The combination was achieved by John Wallis, Isaac Barrow
, and James Gregory
, the latter two proving the second fundamental theorem of calculus
around 1675.
The product rule
and chain rule
, the notion of higher derivatives, Taylor series
, and analytical functions were introduced by Isaac Newton
in an idiosyncratic notation which he used to solve problems of mathematical physics
. In his publications, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid
, and many other problems discussed in his Principia Mathematica (1687). In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series
. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable.
 These ideas were systematized into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism
These ideas were systematized into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism
by Newton. He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for manipulating infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule
and chain rule
, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism, often spending days determining appropriate symbols for concepts.
Leibniz
and Newton
are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics
and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known.
When Newton and Leibniz first published their results, there was great controversy
over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society
. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions
".
Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. One of the first and most complete works on finite and infinitesimal analysis was written in 1748 by Maria Gaetana Agnesi
.
quantities was thought unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle
and Bishop Berkeley
. Berkeley famously described infinitesimals as the ghosts of departed quantities in his book The Analyst
in 1734. Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today.
Several mathematicians, including Maclaurin
, attempted to prove the soundness of using infinitesimals, but it would be 150 years later, due to the work of Cauchy
and Weierstrass
, where a means was finally found to avoid mere "notions" of infinitely small quantities and the foundations of differential and integral calculus were made firm. In Cauchy's writing, we find a versatile spectrum of foundational approaches, including a definition of continuity
in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit
and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities. Bernhard Riemann
used these ideas to give a precise definition of the integral. It was also during this period that the ideas of calculus were generalized to Euclidean space
and the complex plane
.
In modern mathematics, the foundations of calculus are included in the field of real analysis
, which contains full definitions and proof
s of the theorems of calculus. The reach of calculus has also been greatly extended. Henri Lebesgue
invented measure theory and used it to define integrals of all but the most pathological functions. Laurent Schwartz
introduced Distribution
s, which can be used to take the derivative of any function whatsoever.
Limits are not the only rigorous approach to the foundation of calculus. An alternative is Abraham Robinson
's nonstandard analysis. Robinson's approach, developed in the 1960s, uses technical machinery from mathematical logic
to augment the real number system with infinitesimal
and infinite numbers, as in the original Newton-Leibniz conception. The resulting numbers are called hyperreal number
s, and they can be used to give a Leibniz-like development of the usual rules of calculus.
, Greece
, China
, India
, Iraq, Persia
, and Japan
, the modern use of calculus began in Europe
, during the 17th century, when Isaac Newton
and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves.
Applications of differential calculus include computations involving velocity
and acceleration
, the slope
of a curve, and optimization. Applications of integral calculus include computations involving area
, volume
, arc length
, center of mass
, work, and pressure
. More advanced applications include power series and Fourier series
.
Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero
or sums of infinitely many numbers. These questions arise in the study of motion
and area
. The ancient Greek
philosopher Zeno of Elea
gave several famous examples of such paradoxes
. Calculus provides tools, especially the limit
and the infinite series, which resolve the paradoxes.
s. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, 1/2, 1/3, ... and less than any positive real number
. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property
. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis
and smooth infinitesimal analysis
, which provided solid foundations for the manipulation of infinitesimals.
In the 19th century, infinitesimals were replaced by limit
s. Limits describe the value of a function
at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system
. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are the easiest way to provide rigorous foundations for calculus, and for this reason they are the standard approach.
of a function. The process of finding the derivative is called differentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just the derivative of the original function. In mathematical jargon, the derivative is a linear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.)
The most common symbol for a derivative is an apostrophe-like mark called prime
. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function.
If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity
of the ball.
If a function is linear
(that is, if the graph
of the function is a straight line), then the function can be written as , where x is the independent variable, y is the dependent variable, b is the y-intercept, and:

This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in y divided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is
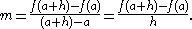
This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point a because it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit
as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero:
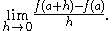
Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f.
Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.
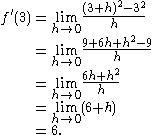
The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function.
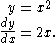
In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example: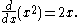
In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative
.
The indefinite integral is the antiderivative
, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of upper- and lower-case letters for a function and its indefinite integral is common in calculus.)
The definite integral inputs a function and outputs a number, which gives the area between the graph of the input and the x-axis. The technical definition of the definite integral is the limit
of a sum of areas of rectangles, called a Riemann sum
.
A motivating example is the distances traveled in a given time.
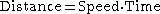
If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum
) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled.
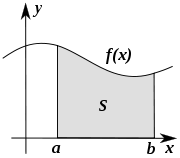 If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s.
If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s.
To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δx and height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δx approaches zero.
The symbol of integration is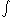 , an elongated S (the S stands for "sum"). The definite integral is written as:
, an elongated S (the S stands for "sum"). The definite integral is written as:
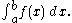
and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation
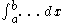
is to be understood as an operator that takes a function as an input and gives a number, the area, as an output; dx is not a number, and is not being multiplied by f(x).
The indefinite integral, or antiderivative, is written:
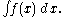
Functions differing by only a constant have the same derivative, and therefore the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter is given by: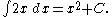
An undetermined constant like C in the antiderivative is known as a constant of integration.
states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration.
The Fundamental Theorem of Calculus states: If a function f is continuous
on the interval [a, b] and if F is a function whose derivative is f on the interval (a, b), then
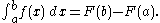
Furthermore, for every x in the interval (a, b),

This realization, made by both Newton
and Leibniz
, who based their results on earlier work by Isaac Barrow
, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivative
s. It is also a prototype solution of a differential equation
. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences.
 Calculus is used in every branch of the physical science
Calculus is used in every branch of the physical science
s, actuarial science
, computer science
, statistics
, engineering
, economics
, business
, medicine
, demography
, and in other fields wherever a problem can be mathematically modeled
and an optimal
solution is desired. It allows one to go from (non-constant) rates of change to the total change or vice versa, and many times in studying a problem we know one and are trying to find the other.
Physics
makes particular use of calculus; all concepts in classical mechanics
and electromagnetism
are interrelated through calculus. The mass
of an object of known density
, the moment of inertia
of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. An example of the use of calculus in mechanics is Newton's second law of motion
: historically stated it expressly uses the term "rate of change" which refers to the derivative saying The rate of change of momentum of a body is equal to the resultant force acting on the body and is in the same direction. Commonly expressed today as Force = Mass × acceleration, it involves differential calculus because acceleration is the time derivative of velocity or second time derivative of trajectory or spatial position. Starting from knowing how an object is accelerating, we use calculus to derive its path.
Maxwell's theory of electromagnetism
and Einstein
's theory of general relativity
are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay. In biology, population dynamics starts with reproduction and death rates to model population changes.
Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra
to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory
to determine the probability of a continuous random variable from an assumed density function. In analytic geometry
, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity
and inflection points.
Green's Theorem
, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter
which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property.
Discrete Green's Theorem, which gives the relationship between a double integral of a function around a simple closed rectangular curve C and a linear combination of the antiderivative's values at corner points along the edge of the curve, allows fast calculation of sums of values in rectangular domains. For example, it can be used to efficiently calculate sums of rectangular domains in images, in order to rapidly extract features and detect object - see also the summed area table
algorithm.
In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow. From the decay laws for a particular drug's elimination from the body, it's used to derive dosing laws. In nuclear medicine, it's used to build models of radiation transport in targeted tumor therapies.
In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost
and marginal revenue
.
Calculus is also used to find approximate solutions to equations; in practice it's the standard way to solve differential equations and do root finding in most applications. Examples are methods such as Newton's method
, fixed point iteration, and linear approximation
. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
focused on limits
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s, integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s, and infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. This subject constitutes a major part of modern mathematics education
Mathematics education
In contemporary education, mathematics education is the practice of teaching and learning mathematics, along with the associated scholarly research....
. It has two major branches, differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
and integral calculus, which are related by the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
. Calculus is the study of change, in the same way that geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
is the study of shape and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
is the study of operations and their application to solving equations. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study of functions and limits, broadly called mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. Calculus has widespread applications in science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and can solve many problems for which algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
alone is insufficient.
Historically, calculus was called "the calculus of infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
s", or "infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
". More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
, variational calculus, lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, pi calculus, and join calculus.
Ancient

Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
calculus, but does not seem to have developed these ideas in a rigorous or systematic way. Calculations of volumes and areas, one goal of integral calculus, can be found in the Egyptian
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
Moscow papyrus
Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
(c. 1820 BC), but the formulas are mere instructions, with no indication as to method, and some of them are wrong. From the age of Greek mathematics
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, Eudoxus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
(c. 408−355 BC) used the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
, which prefigures the concept of the limit, to calculate areas and volumes, while Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
(c. 287−212 BC) developed this idea further
Archimedes' use of infinitesimals
The Method of Mechanical Theorems is a work by Archimedes which contains the first attested explicit use of infinitesimals. The work was originally thought to be lost, but was rediscovered in the celebrated Archimedes Palimpsest...
, inventing heuristics which resemble the methods of integral calculus. The method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
was later reinvented in China
Chinese mathematics
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
by Liu Hui
Liu Hui
Liu Hui was a mathematician of the state of Cao Wei during the Three Kingdoms period of Chinese history. In 263, he edited and published a book with solutions to mathematical problems presented in the famous Chinese book of mathematic known as The Nine Chapters on the Mathematical Art .He was a...
in the 3rd century AD in order to find the area of a circle. In the 5th century AD, Zu Chongzhi
Zu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
established a method which would later be called Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
to find the volume of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
Medieval
In the 14th Century Indian mathematician Madhava of SangamagramaMadhava of Sangamagrama
Mādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
and the Kerala school of astronomy and mathematics stated many components of calculus such as the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, infinite series approximations, an integral test for convergence
Integral test for convergence
In mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. An early form of the test of convergence was developed in India by Madhava in the 14th century, and by his followers at the Kerala School...
, early forms of differentiation, term by term integration, iterative methods for solutions of non-linear equations, and the theory that the area under a curve is its integral. Some consider the Yuktibhāṣā
Yuktibhasa
Yuktibhāṣā also known as Gaṇitanyāyasaṅgraha , is a major treatise on mathematics and astronomy, written by Indian astronomer Jyesthadeva of the Kerala school of mathematics in about AD 1530...
to be the first text on calculus.
Modern
| "The calculus was the first achievement of modern mathematics and it is difficult to overestimate its importance. I think it defines more unequivocally than anything else the inception of modern mathematics, and the system of mathematical analysis, which is its logical development, still constitutes the greatest technical advance in exact thinking." —John von Neumann John von Neumann John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,... |
In Europe, the foundational work was a treatise due to Bonaventura Cavalieri
Bonaventura Cavalieri
Bonaventura Francesco Cavalieri was an Italian mathematician. He is known for his work on the problems of optics and motion, work on the precursors of infinitesimal calculus, and the introduction of logarithms to Italy...
, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimally thin cross-sections. The ideas were similar to Archimedes' in The Method
Archimedes' use of infinitesimals
The Method of Mechanical Theorems is a work by Archimedes which contains the first attested explicit use of infinitesimals. The work was originally thought to be lost, but was rediscovered in the celebrated Archimedes Palimpsest...
, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods could lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first.
The formal study of calculus combined Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
, claiming that he borrowed from Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
, introduced the concept of adequality
Adequality
In the history of infinitesimal calculus, adequality is a technique developed by Pierre de Fermat. Fermat said he borrowed the term from Diophantus. Adequality was a technique first used to find maxima for functions and then adapted to find tangent lines to curves...
, which represented equality up to an infinitesimal error term. The combination was achieved by John Wallis, Isaac Barrow
Isaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
, and James Gregory
James Gregory (astronomer and mathematician)
James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
, the latter two proving the second fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
around 1675.
The product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
and chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the notion of higher derivatives, Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, and analytical functions were introduced by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
in an idiosyncratic notation which he used to solve problems of mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. In his publications, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, and many other problems discussed in his Principia Mathematica (1687). In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable.

Plagiarism
Plagiarism is defined in dictionaries as the "wrongful appropriation," "close imitation," or "purloining and publication" of another author's "language, thoughts, ideas, or expressions," and the representation of them as one's own original work, but the notion remains problematic with nebulous...
by Newton. He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for manipulating infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
and chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism, often spending days determining appropriate symbols for concepts.
Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
and Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known.
When Newton and Leibniz first published their results, there was great controversy
Newton v. Leibniz calculus controversy
The calculus controversy was an argument between 17th-century mathematicians Isaac Newton and Gottfried Leibniz over who had first invented calculus...
over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions
Method of Fluxions
Method of Fluxions is a book by Isaac Newton. The book was completed in 1671, and published in 1736. Fluxions is Newton's term for differential calculus...
".
Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. One of the first and most complete works on finite and infinitesimal analysis was written in 1748 by Maria Gaetana Agnesi
Maria Gaetana Agnesi
Maria Gaetana Agnesi was an Italian linguist, mathematician, and philosopher. Agnesi is credited with writing the first book discussing both differential and integral calculus. She was an honorary member of the faculty at the University of Bologna...
.
Foundations
In mathematics, foundations refers to the rigorous development of a subject from precise axioms and definitions. In early calculus the use of infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
quantities was thought unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle
Michel Rolle
Michel Rolle was a French mathematician. He is best known for Rolle's theorem , and he deserves to be known as the co-inventor in Europe of Gaussian elimination .-Life:...
and Bishop Berkeley
George Berkeley
George Berkeley , also known as Bishop Berkeley , was an Irish philosopher whose primary achievement was the advancement of a theory he called "immaterialism"...
. Berkeley famously described infinitesimals as the ghosts of departed quantities in his book The Analyst
The Analyst
The Analyst, subtitled "A DISCOURSE Addressed to an Infidel MATHEMATICIAN. WHEREIN It is examined whether the Object, Principles, and Inferences of the modern Analysis are more distinctly conceived, or more evidently deduced, than Religious Mysteries and Points of Faith", is a book published by...
in 1734. Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today.
Several mathematicians, including Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
, attempted to prove the soundness of using infinitesimals, but it would be 150 years later, due to the work of Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
and Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, where a means was finally found to avoid mere "notions" of infinitely small quantities and the foundations of differential and integral calculus were made firm. In Cauchy's writing, we find a versatile spectrum of foundational approaches, including a definition of continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities. Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
used these ideas to give a precise definition of the integral. It was also during this period that the ideas of calculus were generalized to Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
In modern mathematics, the foundations of calculus are included in the field of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, which contains full definitions and proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
s of the theorems of calculus. The reach of calculus has also been greatly extended. Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
invented measure theory and used it to define integrals of all but the most pathological functions. Laurent Schwartz
Laurent Schwartz
Laurent-Moïse Schwartz was a French mathematician. He pioneered the theory of distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields medal in 1950 for his work...
introduced Distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s, which can be used to take the derivative of any function whatsoever.
Limits are not the only rigorous approach to the foundation of calculus. An alternative is Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
's nonstandard analysis. Robinson's approach, developed in the 1960s, uses technical machinery from mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
to augment the real number system with infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
and infinite numbers, as in the original Newton-Leibniz conception. The resulting numbers are called hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s, and they can be used to give a Leibniz-like development of the usual rules of calculus.
Significance
While some of the ideas of calculus were developed earlier in EgyptEgyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
, Greece
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, China
Chinese mathematics
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
, India
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
, Iraq, Persia
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
, and Japan
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
, the modern use of calculus began in Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
, during the 17th century, when Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves.
Applications of differential calculus include computations involving velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of a curve, and optimization. Applications of integral calculus include computations involving area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
, arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
, center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
, work, and pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
. More advanced applications include power series and Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
.
Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
or sums of infinitely many numbers. These questions arise in the study of motion
Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
and area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
. The ancient Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
philosopher Zeno of Elea
Zeno of Elea
Zeno of Elea was a pre-Socratic Greek philosopher of southern Italy and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic. He is best known for his paradoxes, which Bertrand Russell has described as "immeasurably subtle and profound".- Life...
gave several famous examples of such paradoxes
Zeno's paradoxes
Zeno's paradoxes are a set of problems generally thought to have been devised by Greek philosopher Zeno of Elea to support Parmenides's doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion is...
. Calculus provides tools, especially the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
and the infinite series, which resolve the paradoxes.
Limits and infinitesimals
Calculus is usually developed by manipulating very small quantities. Historically, the first method of doing so was by infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
s. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, 1/2, 1/3, ... and less than any positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
and smooth infinitesimal analysis
Smooth infinitesimal analysis
Smooth infinitesimal analysis is a mathematically rigorous reformulation of the calculus in terms of infinitesimals. Based on the ideas of F. W. Lawvere and employing the methods of category theory, it views all functions as being continuous and incapable of being expressed in terms of discrete...
, which provided solid foundations for the manipulation of infinitesimals.
In the 19th century, infinitesimals were replaced by limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
s. Limits describe the value of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are the easiest way to provide rigorous foundations for calculus, and for this reason they are the standard approach.
Differential calculus
Differential calculus is the study of the definition, properties, and applications of the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function. The process of finding the derivative is called differentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just the derivative of the original function. In mathematical jargon, the derivative is a linear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.)
The most common symbol for a derivative is an apostrophe-like mark called prime
Prime (symbol)
The prime symbol , double prime symbol , and triple prime symbol , etc., are used to designate several different units, and for various other purposes in mathematics, the sciences and linguistics...
. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function.
If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the ball.
If a function is linear
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
(that is, if the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of the function is a straight line), then the function can be written as , where x is the independent variable, y is the dependent variable, b is the y-intercept, and:

This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in y divided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is
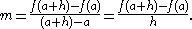
This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point a because it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero:
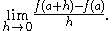
Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f.
Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.
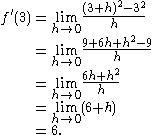
The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function.
Leibniz notation
A common notation, introduced by Leibniz, for the derivative in the example above is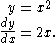
In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example:
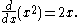
In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
.
Integral calculus
Integral calculus is the study of the definitions, properties, and applications of two related concepts, the indefinite integral and the definite integral. The process of finding the value of an integral is called integration. In technical language, integral calculus studies two related linear operators.The indefinite integral is the antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of upper- and lower-case letters for a function and its indefinite integral is common in calculus.)
The definite integral inputs a function and outputs a number, which gives the area between the graph of the input and the x-axis. The technical definition of the definite integral is the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of a sum of areas of rectangles, called a Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
.
A motivating example is the distances traveled in a given time.
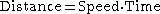
If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled.

To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δx and height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δx approaches zero.
The symbol of integration is
 , an elongated S (the S stands for "sum"). The definite integral is written as:
, an elongated S (the S stands for "sum"). The definite integral is written as: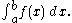
and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation
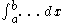
is to be understood as an operator that takes a function as an input and gives a number, the area, as an output; dx is not a number, and is not being multiplied by f(x).
The indefinite integral, or antiderivative, is written:
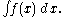
Functions differing by only a constant have the same derivative, and therefore the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter is given by:
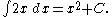
An undetermined constant like C in the antiderivative is known as a constant of integration.
Fundamental theorem
The fundamental theorem of calculusFundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration.
The Fundamental Theorem of Calculus states: If a function f is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the interval [a, b] and if F is a function whose derivative is f on the interval (a, b), then
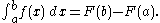
Furthermore, for every x in the interval (a, b),

This realization, made by both Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, who based their results on earlier work by Isaac Barrow
Isaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s. It is also a prototype solution of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences.
Applications

Physical science
Physical science is an encompassing term for the branches of natural science and science that study non-living systems, in contrast to the life sciences...
s, actuarial science
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
, computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, business
Business
A business is an organization engaged in the trade of goods, services, or both to consumers. Businesses are predominant in capitalist economies, where most of them are privately owned and administered to earn profit to increase the wealth of their owners. Businesses may also be not-for-profit...
, medicine
Medicine
Medicine is the science and art of healing. It encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness....
, demography
Demography
Demography is the statistical study of human population. It can be a very general science that can be applied to any kind of dynamic human population, that is, one that changes over time or space...
, and in other fields wherever a problem can be mathematically modeled
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
and an optimal
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
solution is desired. It allows one to go from (non-constant) rates of change to the total change or vice versa, and many times in studying a problem we know one and are trying to find the other.
Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
makes particular use of calculus; all concepts in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
are interrelated through calculus. The mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of an object of known density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. An example of the use of calculus in mechanics is Newton's second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
: historically stated it expressly uses the term "rate of change" which refers to the derivative saying The rate of change of momentum of a body is equal to the resultant force acting on the body and is in the same direction. Commonly expressed today as Force = Mass × acceleration, it involves differential calculus because acceleration is the time derivative of velocity or second time derivative of trajectory or spatial position. Starting from knowing how an object is accelerating, we use calculus to derive its path.
Maxwell's theory of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay. In biology, population dynamics starts with reproduction and death rates to model population changes.
Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
to determine the probability of a continuous random variable from an assumed density function. In analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
and inflection points.
Green's Theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter
Planimeter
A planimeter is a measuring instrument used to determine the area of an arbitrary two-dimensional shape.-Construction:There are several kinds of planimeters, but all operate in a similar way. The precise way in which they are constructed varies, with the main types of mechanical planimeter being...
which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property.
Discrete Green's Theorem, which gives the relationship between a double integral of a function around a simple closed rectangular curve C and a linear combination of the antiderivative's values at corner points along the edge of the curve, allows fast calculation of sums of values in rectangular domains. For example, it can be used to efficiently calculate sums of rectangular domains in images, in order to rapidly extract features and detect object - see also the summed area table
Summed Area Table
A summed area table is an algorithm for quickly and efficiently generating the sum of values in a rectangular subset of a grid...
algorithm.
In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow. From the decay laws for a particular drug's elimination from the body, it's used to derive dosing laws. In nuclear medicine, it's used to build models of radiation transport in targeted tumor therapies.
In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost
Marginal cost
In economics and finance, marginal cost is the change in total cost that arises when the quantity produced changes by one unit. That is, it is the cost of producing one more unit of a good...
and marginal revenue
Marginal revenue
In microeconomics, marginal revenue is the extra revenue that an additional unit of product will bring. It is the additional income from selling one more unit of a good; sometimes equal to price...
.
Calculus is also used to find approximate solutions to equations; in practice it's the standard way to solve differential equations and do root finding in most applications. Examples are methods such as Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
, fixed point iteration, and linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments.
Lists
- List of calculus topics
- List of derivatives and integrals in alternative calculi
- List of differentiation identities
- Publications in calculus
- Table of integrals
Related topics
- Calculus of finite differences
- Calculus with polynomials
- Complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
- Differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
- Differential geometryDifferential geometry and topologyDifferential geometry is a mathematical discipline that uses the techniques of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis...
- Elementary Calculus: An Infinitesimal ApproachElementary Calculus: An Infinitesimal ApproachElementary Calculus: An Infinitesimal approach is a textbook by H. Jerome Keisler. The subtitle alludes to the infinitesimal numbers of Abraham Robinson's non-standard analysis...
- Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
- Integral equationIntegral equationIn mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
- Mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
- Multivariable calculusMultivariable calculusMultivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
- Non-classical analysisNon-classical analysisIn mathematics, non-classical analysis is any system of analysis, other than classical real analysis, and complex, vector, tensor, etc., analysis based upon it.Such systems include:...
- Non-standard analysisNon-standard analysisNon-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
- Non-standard calculusNon-standard calculusIn mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
- PrecalculusPrecalculusIn American mathematics education, precalculus , an advanced form of secondary school algebra, is a foundational mathematical discipline. It is also called Introduction to Analysis. In many schools, precalculus is actually two separate courses: Algebra and Trigonometry...
(mathematical educationMathematics educationIn contemporary education, mathematics education is the practice of teaching and learning mathematics, along with the associated scholarly research....
) - Product integralProduct integralProduct integrals are a counterpart of standard integrals of infinitesimal calculus. They were first developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations...
- Stochastic calculusStochastic calculusStochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
- Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
Books
- Larson, RonRon Larson (mathematician)Roland "Ron" Edwin Larson is a professor of mathematics at Penn State Erie, The Behrend College, Pennsylvania. He is best known for being the author of a series of widely-used mathematics textbooks ranging from middle school through the second year of college.-Early life:Ron Larson was born in...
, Bruce H. Edwards (2010). "Calculus", 9th ed., Brooks Cole Cengage Learning. ISBN 9780547167022 - McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 9781891389245
- Stewart, JamesJames Stewart (mathematician)James Drewry Stewart is a Canadian professor emeritus of mathematics at McMaster University. Stewart received his M.S. at Stanford University and his Ph.D from the University of Toronto. He worked for two years as a postdoctoral fellow at the University of London...
(2008). Calculus: Early Transcendentals, 6th ed., Brooks Cole Cengage Learning. ISBN 9780495011668 - Thomas, George B.George B. ThomasGeorge Brinton Thomas, Jr. was a professor of mathematics at MIT. He is best known for being the author of a widely-used calculus textbook.-Early life:Born in Boise, Idaho, Thomas' early years were difficult...
, Maurice D. Weir, Joel Hass, Frank R. Giordano (2008), "Calculus", 11th ed., Addison-Wesley. ISBN 0-321-48987-X
Further reading
- Boyer, Carl BenjaminCarl Benjamin BoyerCarl Benjamin Boyer was a historian of sciences, and especially mathematics. David Foster Wallace called him the "Gibbon of math history"....
(1949). The History of the Calculus and its Conceptual Development. Hafner. Dover edition 1959, ISBN 0-486-60509-4 - Courant, RichardRichard CourantRichard Courant was a German American mathematician.- Life :Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there...
ISBN 978-3540650584 Introduction to calculus and analysis 1. - Edmund LandauEdmund LandauEdmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
. ISBN 0-8218-2830-4 Differential and Integral Calculus, American Mathematical SocietyAmerican Mathematical SocietyThe American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
. - Robert A. Adams. (1999). ISBN 978-0-201-39607-2 Calculus: A complete course.
- Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7.
- John Lane BellJohn Lane BellJohn Bell is Professor of Philosophy at the University of Western Ontario in Canada. He is an outstanding figure in mathematical logic and philosophy...
: A Primer of Infinitesimal Analysis, Cambridge University Press, 1998. ISBN 978-0-521-62401-5. Uses synthetic differential geometrySynthetic differential geometryIn mathematics, synthetic differential geometry is a reformulation of differential geometry in the language of topos theory, in the context of an intuitionistic logic characterized by a rejection of the law of excluded middle. There are several insights that allow for such a reformulation...
and nilpotent infinitesimals. - Florian CajoriFlorian CajoriFlorian Cajori was one of the most celebrated historians of mathematics in his day.- Biography :...
, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1–46. - Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton Univ. Press, 2004.
- Cliff Pickover. (2003). ISBN 978-0-471-26987-8 Calculus and Pizza: A Math Cookbook for the Hungry Mind.
- Michael SpivakMichael SpivakMichael David Spivak is a mathematician specializing in differential geometry, an expositor of mathematics, and the founder of Publish-or-Perish Press. He is the author of the five-volume Comprehensive Introduction to Differential Geometry. He received a Ph.D...
. (September 1994). ISBN 978-0-914098-89-8 Calculus. Publish or Perish publishing. - Tom M. ApostolTom M. ApostolTom Mike Apostol is a Greek-American analytic number theorist and professor at the California Institute of Technology.He was born in Helper, Utah in 1923. His parents, Emmanouil Apostolopoulos and Efrosini Papathanasopoulos, originated from Greece. Mr...
. (1967). ISBN 9780471000051 Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley. - Tom M. ApostolTom M. ApostolTom Mike Apostol is a Greek-American analytic number theorist and professor at the California Institute of Technology.He was born in Helper, Utah in 1923. His parents, Emmanouil Apostolopoulos and Efrosini Papathanasopoulos, originated from Greece. Mr...
. (1969). ISBN 9780471000075 Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley. - Silvanus P. ThompsonSilvanus P. ThompsonSilvanus Phillips Thompson FRS was a professor of physics at the City and Guilds Technical College in Finsbury, England. He was elected to the Royal Society in 1891 and was known for his work as an electrical engineer and as an author...
and Martin GardnerMartin GardnerMartin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
. (1998). ISBN 978-0-312-18548-0 Calculus Made Easy. - Mathematical Association of AmericaMathematical Association of AmericaThe Mathematical Association of America is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university, college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists;...
. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252. - Thomas/Finney. (1996). ISBN 978-0-201-53174-9 Calculus and Analytic geometry 9th, Addison Wesley.
- Weisstein, Eric W. "Second Fundamental Theorem of Calculus." From MathWorld—A Wolfram Web Resource.
- Howard Anton,Irl Bivens,Stephen Davis:"Calculus",John Willey and Sons Pte. Ltd.,2002.ISBN 978-81-265-1259-1
Online books
- Crowell, B. (2003). "Calculus" Light and Matter, Fullerton. Retrieved 6 May 2007 from http://www.lightandmatter.com/calc/calc.pdf
- Garrett, P. (2006). "Notes on first year calculus" University of Minnesota. Retrieved 6 May 2007 from
http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf - Faraz, H. (2006). "Understanding Calculus" Retrieved 6 May 2007 from Understanding Calculus, URL http://www.understandingcalculus.com/ (HTML only)
- Keisler, H. J. (2000). "Elementary Calculus: An Approach Using Infinitesimals" Retrieved 29 August 2010 from
http://www.math.wisc.edu/~keisler/calc.html - Mauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. Retrieved 6 May 2007 from
http://www.cacr.caltech.edu/~sean/applied_math.pdf - Sloughter, Dan (2000). "Difference Equations to Differential Equations: An introduction to calculus". Retrieved 17 March 2009 from http://synechism.org/drupal/de2de/
- Stroyan, K.D. (2004). "A brief introduction to infinitesimal calculus" University of Iowa. Retrieved 6 May 2007 from http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm (HTML only)
- Strang, G. (1991). "Calculus" Massachusetts Institute of Technology. Retrieved 6 May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm
- Smith, William V. (2001). "The Calculus" Retrieved 4 July 2008 http://www.math.byu.edu/~smithw/Calculus/ (HTML only).
External links
- Calculus Made Easy (1914) by Silvanus P. Thompson Full text in PDF
- Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sites
- COW: Calculus on the Web at Temple University – contains resources ranging from pre-calculus and associated algebra
- Earliest Known Uses of Some of the Words of Mathematics: Calculus & Analysis
- Online Integrator (WebMathematica) from Wolfram Research
- The Role of Calculus in College Mathematics from ERICDigests.org
- OpenCourseWare Calculus from the Massachusetts Institute of TechnologyMassachusetts Institute of TechnologyThe Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
- Infinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, Michiel Hazewinkel ed. .
- Elements of Calculus I and Calculus II for Business, OpenCourseWareOpenCourseWareOpenCourseWare, or OCW, is a term applied to course materials created by universities and shared freely with the world via the internet. The movement started in 1999 when the University of Tübingen in Germany published videos of lectures online in the context of its timms initiative...
from the University of Notre DameUniversity of Notre DameThe University of Notre Dame du Lac is a Catholic research university located in Notre Dame, an unincorporated community north of the city of South Bend, in St. Joseph County, Indiana, United States...
with activities, exams and interactive applets. - Calculus for Beginners and Artists by Daniel Kleitman, MIT
- Calculus Problems and Solutions by D. A. Kouba
- Solved problems in calculus
- Video explanations and solved problems in calculus Raymond, CUNY

