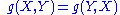Pseudo-Riemannian manifold
Encyclopedia
In differential geometry, a pseudo-Riemannian manifold (also called a semi-Riemannian manifold) is a generalization of a Riemannian manifold
. It is one of many mathematical objects named after Bernhard Riemann
. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the metric tensor
need not be positive-definite
. Instead a weaker condition of nondegeneracy is imposed.
is a space which is locally similar to a Euclidean space
. In an n-dimensional Euclidean space any point can be specified by n real numbers. These are called the coordinates of the point.
An n-dimensional differentiable manifold is a generalisation of n-dimensional Euclidean space. In a manifold it may only be possible to define coordinates locally. This is achieved by defining coordinate patches: subsets of the manifold which can be mapped into n-dimensional Euclidean space.
See Manifold
, differentiable manifold
, coordinate patch for more details.
 in an
in an  -dimensional differentiable manifold
-dimensional differentiable manifold  is a tangent space
is a tangent space
(denoted ). This is an
). This is an  -dimensional vector space
-dimensional vector space
whose elements can be thought of as equivalence classes of curves passing through the point .
.
A metric tensor
is a non-degenerate, smooth, symmetric, bilinear map which assigns a real number
to pairs of tangent vectors at each tangent space of the manifold. Denoting the metric tensor by we can express this as
we can express this as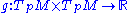 .
.
The map is symmetric and bilinear so if are tangent vectors at a point
are tangent vectors at a point  to the manifold
to the manifold  then we have
then we have
for any real number .
.
That is non-degenerate means there are no non-zero
is non-degenerate means there are no non-zero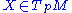 such that
such that 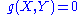 for all
for all 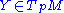 .
.
of the metric denotes the number of positive and negative eigenvalues, this quantity is independent of the chosen coordinate system by Sylvester's rigidity theorem
and locally non-decreasing.
If the metric has p positive eigenvalues and q negative eigenvalues then the metric signature is (p, q). For a non-degenerate metric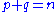 .
.
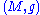 is a differentiable manifold
is a differentiable manifold
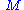 equipped with a non-degenerate, smooth, symmetric metric tensor
equipped with a non-degenerate, smooth, symmetric metric tensor
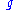 which, unlike a Riemannian metric, need not be positive-definite
which, unlike a Riemannian metric, need not be positive-definite
, but must be non-degenerate. Such a metric is called a pseudo-Riemannian metric and its values can be positive, negative or zero.
The signature of a pseudo-Riemannian metric is (p, q) where both p and q are non-negative.
). Such metrics are called Lorentzian metrics. They are named after the physicist Hendrik Lorentz
.
.
A principal assumption of general relativity
is that spacetime
can be modeled as a 4-dimensional Lorentzian manifold of signature (3, 1) or, equivalently, (1, 3). Unlike Riemannian manifolds with positive-definite metrics, a signature of (p, 1) or (1, q) allows tangent vectors to be classified into timelike, null or spacelike (see Causal structure
).
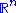 can be thought of as the model Riemannian manifold
can be thought of as the model Riemannian manifold
, Minkowski space
 with the flat Minkowski metric is the model Lorentzian manifold. Likewise, the model space for a pseudo-Riemannian manifold of signature (p, q) is
with the flat Minkowski metric is the model Lorentzian manifold. Likewise, the model space for a pseudo-Riemannian manifold of signature (p, q) is 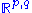 with the metric
with the metric
Some basic theorems of Riemannian geometry can be generalized to the pseudo-Riemannian case. In particular, the fundamental theorem of Riemannian geometry
is true of pseudo-Riemannian manifolds as well. This allows one to speak of the Levi-Civita connection
on a pseudo-Riemannian manifold along with the associated curvature tensor
. On the other hand, there are many theorems in Riemannian geometry which do not hold in the generalized case. For example, it is not true that every smooth manifold admits a pseudo-Riemannian metric of a given signature; there are certain topological
obstructions. Furthermore, a submanifold
does not always inherit the structure of a pseudo-Riemannian manifold; for example, the metric tensor become zero on any light-like curve
.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. It is one of many mathematical objects named after Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
need not be positive-definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
. Instead a weaker condition of nondegeneracy is imposed.
Manifolds
In differential geometry, a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
is a space which is locally similar to a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In an n-dimensional Euclidean space any point can be specified by n real numbers. These are called the coordinates of the point.
An n-dimensional differentiable manifold is a generalisation of n-dimensional Euclidean space. In a manifold it may only be possible to define coordinates locally. This is achieved by defining coordinate patches: subsets of the manifold which can be mapped into n-dimensional Euclidean space.
See Manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, coordinate patch for more details.
Tangent spaces and metric tensors
Associated with each point in an
in an  -dimensional differentiable manifold
-dimensional differentiable manifold  is a tangent space
is a tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
(denoted
 ). This is an
). This is an  -dimensional vector space
-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
whose elements can be thought of as equivalence classes of curves passing through the point
 .
.A metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is a non-degenerate, smooth, symmetric, bilinear map which assigns a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
to pairs of tangent vectors at each tangent space of the manifold. Denoting the metric tensor by
 we can express this as
we can express this as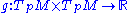 .
.The map is symmetric and bilinear so if
 are tangent vectors at a point
are tangent vectors at a point  to the manifold
to the manifold  then we have
then we have
for any real number
 .
.That
 is non-degenerate means there are no non-zero
is non-degenerate means there are no non-zero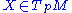 such that
such that 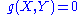 for all
for all 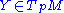 .
.Metric signatures
For an n-dimensional manifold the metric tensor (in a fixed coordinate system) has n eigenvalues. If the metric is non-degenerate then none of these eigenvalues are zero. The signatureMetric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
of the metric denotes the number of positive and negative eigenvalues, this quantity is independent of the chosen coordinate system by Sylvester's rigidity theorem
Sylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
and locally non-decreasing.
If the metric has p positive eigenvalues and q negative eigenvalues then the metric signature is (p, q). For a non-degenerate metric
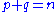 .
.Definition
A pseudo-Riemannian manifold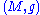 is a differentiable manifold
is a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
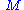 equipped with a non-degenerate, smooth, symmetric metric tensor
equipped with a non-degenerate, smooth, symmetric metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
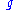 which, unlike a Riemannian metric, need not be positive-definite
which, unlike a Riemannian metric, need not be positive-definiteDefinite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
, but must be non-degenerate. Such a metric is called a pseudo-Riemannian metric and its values can be positive, negative or zero.
The signature of a pseudo-Riemannian metric is (p, q) where both p and q are non-negative.
Lorentzian manifold
A Lorentzian manifold is an important special case of a pseudo-Riemannian manifold in which the signature of the metric is (1, n−1) (or sometimes (n−1, 1), see sign conventionSign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
). Such metrics are called Lorentzian metrics. They are named after the physicist Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
.
Applications in physics
After Riemannian manifolds, Lorentzian manifolds form the most important subclass of pseudo-Riemannian manifolds. They are important because of their physical applications to the theory of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
A principal assumption of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
is that spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
can be modeled as a 4-dimensional Lorentzian manifold of signature (3, 1) or, equivalently, (1, 3). Unlike Riemannian manifolds with positive-definite metrics, a signature of (p, 1) or (1, q) allows tangent vectors to be classified into timelike, null or spacelike (see Causal structure
Causal structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
).
Properties of pseudo-Riemannian manifolds
Just as Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
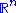 can be thought of as the model Riemannian manifold
can be thought of as the model Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
 with the flat Minkowski metric is the model Lorentzian manifold. Likewise, the model space for a pseudo-Riemannian manifold of signature (p, q) is
with the flat Minkowski metric is the model Lorentzian manifold. Likewise, the model space for a pseudo-Riemannian manifold of signature (p, q) is 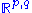 with the metric
with the metric
Some basic theorems of Riemannian geometry can be generalized to the pseudo-Riemannian case. In particular, the fundamental theorem of Riemannian geometry
Fundamental theorem of Riemannian geometry
In Riemannian geometry, the fundamental theorem of Riemannian geometry states that on any Riemannian manifold there is a unique torsion-free metric connection, called the Levi-Civita connection of the given metric...
is true of pseudo-Riemannian manifolds as well. This allows one to speak of the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
on a pseudo-Riemannian manifold along with the associated curvature tensor
Curvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
. On the other hand, there are many theorems in Riemannian geometry which do not hold in the generalized case. For example, it is not true that every smooth manifold admits a pseudo-Riemannian metric of a given signature; there are certain topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
obstructions. Furthermore, a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
does not always inherit the structure of a pseudo-Riemannian manifold; for example, the metric tensor become zero on any light-like curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
.
See also
- SpacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
- Hyperbolic partial differential equationHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
- Causality conditionsCausality conditionsIn the study of Lorentzian manifold spacetimes there exists a hierarchy of causality conditions which are important in proving mathematical theorems about the global structure of such manifolds. These conditions were collected during the late 1970s....
- Globally hyperbolic manifold