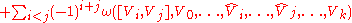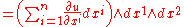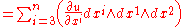Exterior derivative
Encyclopedia
In differential geometry, the exterior derivative extends the concept of the differential
of a function, which is a 1-form, to differential form
s of higher degree. Its current form was invented by Élie Cartan
.
The exterior derivative d has the property that and is the differential
(coboundary) used to define de Rham cohomology
on forms. Integration of forms gives a natural homomorphism from the de Rham cohomology to the singular cohomology of a smooth manifold. The theorem of de Rham shows that this map is actually an isomorphism. In this sense, the exterior derivative is the "dual" of the boundary map on singular simplices.
such that for every smooth vector field
X, , where Xƒ is the directional derivative of ƒ in the direction of X. Thus the exterior derivative of a function (or 0-form) is a one-form.
The second defining property holds in more generality: in fact, for any k-form α. This is part of the Poincaré lemma. The third defining property implies as a special case that if ƒ is a function and α a k-form, then because functions are forms of degree 0.

over Rn is defined as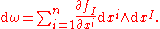
For general k-forms (where the components of the multi-index I run over all the values in {1, ..., n}), the definition of the exterior derivative is extended linear
ly. Note that whenever i is one of the components of the multi-index I then (see wedge product).
The definition of the exterior derivative in local coordinates follows from the preceding definition. Indeed, if , then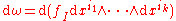
Differential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
of a function, which is a 1-form, to differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s of higher degree. Its current form was invented by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
.
The exterior derivative d has the property that and is the differential
Differential
-Mathematics:* Differential comprises multiple related meanings of the word, both in calculus and differential geometry, such as an infinitesimal change in the value of a function* Differential algebra* Differential calculus...
(coboundary) used to define de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
on forms. Integration of forms gives a natural homomorphism from the de Rham cohomology to the singular cohomology of a smooth manifold. The theorem of de Rham shows that this map is actually an isomorphism. In this sense, the exterior derivative is the "dual" of the boundary map on singular simplices.
Definition
The exterior derivative of a differential form of degree k is a differential form of degree There are a variety of equivalent definitions of the exterior derivative.Exterior derivative of a function
If ƒ is a smooth function, then the exterior derivative of ƒ is the differential of ƒ. That is, dƒ is the unique one-formOne-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
such that for every smooth vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X, , where Xƒ is the directional derivative of ƒ in the direction of X. Thus the exterior derivative of a function (or 0-form) is a one-form.
Exterior derivative of a k-form
The exterior derivative is defined to be the unique R-linear mapping from k-forms to (k+1)-forms satisfying the following properties:- dƒ is the differential of ƒ for smooth functions ƒ.
- for any smooth function ƒ.
- where α is a p-form. That is to say, d is an antiderivation of degree 1 on the exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of differential forms.
The second defining property holds in more generality: in fact, for any k-form α. This is part of the Poincaré lemma. The third defining property implies as a special case that if ƒ is a function and α a k-form, then because functions are forms of degree 0.
Exterior derivative in local coordinates
Alternatively, one can work entirely in a local coordinate system (x1,...,xn). First, the coordinate differentials dx1,...,dxn form a basic set of one-forms within the coordinate chart. Given a multi-index with for , the exterior derivative of a k-form
over Rn is defined as
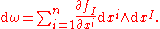
For general k-forms (where the components of the multi-index I run over all the values in {1, ..., n}), the definition of the exterior derivative is extended linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
ly. Note that whenever i is one of the components of the multi-index I then (see wedge product).
The definition of the exterior derivative in local coordinates follows from the preceding definition. Indeed, if , then
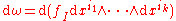
-

-

-

-
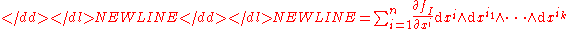
Here, we have here interpreted ƒI as a zero-form, and then applied the properties of the exterior derivative.
Invariant formula
Alternatively, an explicit formula can be given for the exterior derivative of a k-form ω, when paired with k+1 arbitrary smooth vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s V0,V1, ..., Vk:
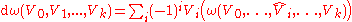
where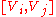 denotes Lie bracketLie bracket of vector fieldsIn the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
denotes Lie bracketLie bracket of vector fieldsIn the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
and the hat denotes the omission of that element: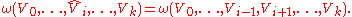
In particular, for 1-forms we have: , where X and Y are vector fields.
Examples
1
Consider over a 1-form basis .
The exterior derivative is:

The last formula follows easily from the properties of the wedge product. Namely,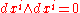 .
.
2
For a 1-form defined over R2. We have, by applying the above formula to each term (consider and ) the following sum,

Closed and exact forms
Differential forms in the kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of d are called closed formClosed form-Maths:* Closed-form expression, a finitary expression* Closed differential form, a differential form \alpha with the property that d\alpha = 0-Poetry:* In poetry analysis, a type of poetry that exhibits regular structure, such as meter or a rhyming pattern;...
s. The imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of d are called exact forms. Closed and exact forms are related, because of the identity for any k-form α. This implies that every exact form is closed. The converse is true in contractible regions, by the converse to the Poincaré lemma.
Naturality
The exterior derivative is natural. If is a smooth map and Ωk is the contravariant smooth functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
that assigns to each manifold the space of k-forms on the manifold, then the following diagram commutes
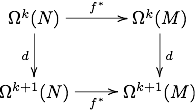
so where ƒ* denotes the pullback of ƒ. This follows from that ƒ*ω(·), by definition, is ω(ƒ*(·)), ƒ* being the pushforward of ƒ. Thus d is a natural transformationNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from Ωk to Ωk+1.
The exterior derivative in calculus
Most vector calculus operators are special cases of, or have close relationships to, the notion of exterior differentiation.
Gradient
A smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
f: Rn → R is a 0-form. The exterior derivative of this 0-form is the 1-form
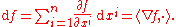
That is, the form dƒ acts on any vector field V by outputting, at each point, the scalar product of V with the gradient ∇ƒ of ƒ.
The 1-form dƒ is a section of the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, that gives a local linear approximation to ƒ in the cotangent space at each point.
Divergence
A vector field V = (v1, v2, ... vn) on Rn has a corresponding (n-1)-form
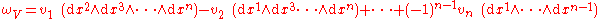

where denotes the omission of that element.
denotes the omission of that element.
(For instance, when n = 3, in three-dimensional space, the 2-form ωV is locally the scalar triple product with V.) The integral of ωV over a hypersurface is the fluxFluxIn the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
of V over that hypersurface.
The exterior derivative of this (n−1)-form is the n-form
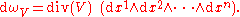
Curl
A vector field V on Rn also has a corresponding 1-form
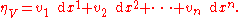 ,
,
Locally, ηV is the dot product with V. The integral of ηV along a path is the workMechanical workIn physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
done against -V along that path.
When n = 3, in three-dimensional space, the exterior derivative of the 1-form ηV is the 2-form
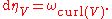
Invariant formulations of grad, curl, div, and Laplacian
The three operators above can be written in coordinate-free notation as follows:
-
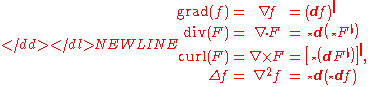
where is the Hodge star operatorHodge dualIn mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
is the Hodge star operatorHodge dualIn mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
and and
and  are the musical isomorphismMusical isomorphismIn mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
are the musical isomorphismMusical isomorphismIn mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
s.
See also
- Exterior covariant derivativeExterior covariant derivativeIn mathematics, the exterior covariant derivative, sometimes also covariant exterior derivative, is a very useful notion for calculus on manifolds, which makes it possible to simplify formulas which use a principal connection....
- de Rham complex
- Discrete exterior calculusDiscrete exterior calculusIn mathematics, the discrete exterior calculus is the extension of the exterior calculus to discrete spaces including graphs and finite element meshes. DEC methods have proved to be very powerful in improving and analyzing finite element methods: for instance, DEC-based methods allow the use of...
- Green's theoremGreen's theoremIn mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
- Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
- Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
- Exterior covariant derivative
-
-
-
-