
Submanifold
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a submanifold of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S which itself has the structure of a manifold, and for which the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required. Different authors often have different definitions.
Formal definition
In the following we assume all manifolds are differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s of class Cr for a fixed r ≥ 1, and all morphisms are differentiable of class Cr.
Immersed submanifolds

More narrowly, one can require that the map i: N → M be an inclusion (one-to-one), in which we call it an injective immersion, and define an immersed submanifold to be the image subset S together with a topology and differential structure
Differential structure
In mathematics, an n-dimensional differential structure on a set M makes M into an n-dimensional differential manifold, which is a topological manifold with some additional structure that allows us to do differential calculus on the manifold...
such that S is a manifold and the inclusion i is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
: this is just the topology on N, which in general will not agree with the subset topology: in general the subset S is not a submanifold of M, in the subset topology.
Given any injective immersion f : N → M the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of N in M can be uniquely given the structure of an immersed submanifold so that f : N → f(N) is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. It follows that immersed submanifolds are precisely the images of injective immersions.
The submanifold topology on an immersed submanifold need not be the relative topology inherited from M. In general, it will be finer than the subspace topology (i.e. have more open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s).
Immersed submanifolds occur in the theory of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s where Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
s are naturally immersed submanifolds.
Embedded submanifolds
An embedded submanifold (also called a regular submanifold), is an immersed submanifold for which the inclusion map is a topological embedding. That is, the submanifold topology on S is the same as the subspace topology.Given any embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
f : N → M of a manifold N in M the image f(N) naturally has the structure of an embedded submanifold. That is, embedded submanifolds are precisely the images of embeddings.
There is an intrinsic definition of an embedded submanifold which is often useful. Let M be an n-dimensional manifold, and let k be an integer such that 0 ≤ k ≤ n. A k-dimensional embedded submanifold of M is a subspace S ⊂ M such that for every point p ∈ S there exists a chart (U ⊂ M, φ : U → Rn) containing p such that φ(S ∩ U) is the intersection of a k-dimensional plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
with φ(U). The pairs (S ∩ U, φ|S ∩ U) form an atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
for the differential structure on S.
Alexander's theorem and jordan-schoenflies are good examples of smooth embeddings.
Other variations
There are some other variations of submanifolds used in the literature. Sharpe (1997) defines a type of submanifold which lies somewhere between an embedded submanifold and an immersed submanifold.Properties
Given any immersed submanifold S of M, the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to a point p in S can naturally be thought of as a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the tangent space to p in M. This follows from the fact that the inclusion map is an immersion and provides an injection
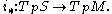
Suppose S is an immersed submanifold of M. If the inclusion map i : S → M is closed then S is actually an embedded submanifold of M. Conversely, if S is an embedded submanifold which is also a closed subset then the inclusion map is closed. The inclusion map i : S → M is closed if and only if it is a proper map
Proper map
In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
(i.e. inverse images of compact sets are compact). If i is closed then S is called a closed embedded submanifold of M. Closed embedded submanifolds form the nicest class of submanifolds.
Submanifolds of Euclidean space
Manifolds are often defined as embedded submanifolds of Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, so this forms a very important special case. By the Whitney embedding theorem any second-countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
smooth n-manifold can be smoothly embedded in R2n.

