Equivariant
Encyclopedia
In mathematics
, an equivariant map is a function
between two sets that commutes with the action of a group
. Specifically, let G be a group
and let X and Y be two associated G-sets
. A function f : X → Y is said to be equivariant if
for all g ∈ G and all x in X. Note that if one or both of the actions are right actions the equivariance condition must be suitably modified:
Equivariant maps are homomorphism
s in the category
of G-sets (for a fixed G). Hence they are also known as G-maps or G-homomorphisms. Isomorphism
s of G-sets are simply bijective equivariant maps.
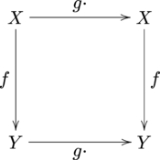
The equivariance condition can also be understood as the following commutative diagram
. Note that denotes the map that takes an element
denotes the map that takes an element  and returns
and returns  .
.
Specifically, if X and Y are the representation spaces of two linear representations of G then a linear map f : X → Y is called an intertwiner of the representations if it commutes with the action of G. Thus an intertwiner is an equivariant map in the special case of two linear representations/actions.
Alternatively, an intertwiner for representations of G over a field
K is the same thing as a module homomorphism
of K[G]-modules
, where K[G] is the group ring
of G.
Under some conditions, if X and Y are both irreducible representations, then an intertwiner (other than the zero map) only exists if the two representations are equivalent (that is, are isomorphic as modules
). That intertwiner is then unique up to
a multiplicative factor (a non-zero scalar
from K). These properties hold when the image of K[G] is a simple algebra, with centre K (by what is called Schur's Lemma
: see simple module
). As a consequence, in important cases the construction of an intertwiner is enough to show the representations are effectively the same.
in a straightforward manner. Every group G can be viewed as a category with a single object (morphism
s in this category are just the elements of G). Given an arbitrary category C, a representation of G in the category C is a functor
from G to C. Such a functor selects an object of C and a subgroup
of automorphism
s of that object. For example, a G-set is equivalent to a functor from G to the category of sets
, Set, and a linear representation is equivalent to a functor to the category of vector spaces
over a field, VectK.
Given two representations, ρ and σ, of G in C, an equivariant map between those representations is simply a natural transformation
from ρ to σ. Using natural transformations as morphisms, one can form the category of all representations of G in C. This is just the functor category
CG.
For another example, take C = Top, the category of topological spaces
. A representation of G in Top is a topological space
on which G acts continuously
. An equivariant map is then a continuous map f : X → Y between representations which commutes with the action of G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an equivariant map is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between two sets that commutes with the action of a group
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. Specifically, let G be a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and let X and Y be two associated G-sets
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. A function f : X → Y is said to be equivariant if
- f(g·x) = g·f(x)
for all g ∈ G and all x in X. Note that if one or both of the actions are right actions the equivariance condition must be suitably modified:
- f(x·g) = f(x)·g ; (right-right)
- f(x·g) = g−1·f(x) ; (right-left)
- f(g·x) = f(x)·g−1 ; (left-right)
Equivariant maps are homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of G-sets (for a fixed G). Hence they are also known as G-maps or G-homomorphisms. Isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s of G-sets are simply bijective equivariant maps.
The equivariance condition can also be understood as the following commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
. Note that
 denotes the map that takes an element
denotes the map that takes an element  and returns
and returns  .
.
Intertwiners
A completely analogous definition holds for the case of linear representations of G.Specifically, if X and Y are the representation spaces of two linear representations of G then a linear map f : X → Y is called an intertwiner of the representations if it commutes with the action of G. Thus an intertwiner is an equivariant map in the special case of two linear representations/actions.
Alternatively, an intertwiner for representations of G over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is the same thing as a module homomorphism
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of K[G]-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, where K[G] is the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of G.
Under some conditions, if X and Y are both irreducible representations, then an intertwiner (other than the zero map) only exists if the two representations are equivalent (that is, are isomorphic as modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
). That intertwiner is then unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a multiplicative factor (a non-zero scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
from K). These properties hold when the image of K[G] is a simple algebra, with centre K (by what is called Schur's Lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
: see simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
). As a consequence, in important cases the construction of an intertwiner is enough to show the representations are effectively the same.
Categorical description
Equivariant maps can be generalized to arbitrary categoriesCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
in a straightforward manner. Every group G can be viewed as a category with a single object (morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s in this category are just the elements of G). Given an arbitrary category C, a representation of G in the category C is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from G to C. Such a functor selects an object of C and a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of that object. For example, a G-set is equivalent to a functor from G to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, Set, and a linear representation is equivalent to a functor to the category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
over a field, VectK.
Given two representations, ρ and σ, of G in C, an equivariant map between those representations is simply a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from ρ to σ. Using natural transformations as morphisms, one can form the category of all representations of G in C. This is just the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
CG.
For another example, take C = Top, the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. A representation of G in Top is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on which G acts continuously
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. An equivariant map is then a continuous map f : X → Y between representations which commutes with the action of G.

