Orbifold
Encyclopedia
In the mathematical disciplines of topology
, geometry
, and geometric group theory
, an orbifold (for "orbit-manifold") is a generalization of a manifold
. It is a topological space (called the underlying space) with an orbifold structure (see below).
The underlying space locally looks like the quotient space
of a
Euclidean space
under the linear action of a finite group
.
Definitions of orbifold have been given several times: by Satake
in the context of automorphic form
s in the 1950s under the name V-manifold; by Thurston
in the context of the geometry of 3-manifold
s in the 1970s when he coined the name orbifold, after a vote by his students; and by Haefliger
in the 1980s in the context of Gromov's programme on CAT(k) space
s under the name orbihedron. The definition of Thurston will be described here: it is the most widely used and is applicable in all cases.
Mathematically, orbifolds arose first as surfaces with singular points long before they were formally defined. One of the first classical examples arose in the theory of modular forms with the action of the modular group
SL(2,Z) on the upper half-plane: a version of the Riemann–Roch theorem holds after the quotient is compactified by the addition of two orbifold cusp points. In 3-manifold
theory, the theory of Seifert fiber spaces, initiated by Seifert
, can be phrased in terms of 2-dimensional orbifolds. In geometric group theory
, post-Gromov, discrete groups have been studied in terms of the local curvature properties of orbihedra and their covering spaces.
In string theory
, the word "orbifold" has a slightly different meaning, discussed in detail below. In conformal field theory
, a mathematical part of string theory, it is often used to refer to the theory attached to the fixed point subalgebra of a vertex algebra under the action of a finite group of automorphisms.
The main example of underlying space is a quotient space of a manifold under the properly discontinuous
action of a possibly infinite group
of diffeomorphism
s with finite isotropy subgroups. In particular this applies to any action of a finite group
; thus a manifold with boundary carries a natural orbifold structure, since it is the quotient of its double by an action of Z2.
Similarly the quotient space of a manifold by a smooth proper action of S1 carries the structure of an orbifold.
Orbifold structure gives a natural stratification
by open manifolds on its underlying space, where one stratum corresponds to a set of singular points of the same type.
It should be noted that one topological space can carry many different orbifold structures.
For example, consider the orbifold O associated with a factor space of the 2-sphere along a rotation by
; it is homeomorphic to the 2-sphere, but the natural orbifold structure is different.
It is possible to adopt most of the characteristics of manifolds to orbifolds and these characteristics are usually different from correspondent characteristics of underlying space.
In the above example, the orbifold fundamental group
of O is Z2
and its orbifold Euler characteristic
is 1.
An n-dimensional orbifold is a Hausdorff topological space X, called the underlying space, with a covering by a collection of open sets Ui, closed under finite intersection. For each Ui, there is
The collection of orbifold charts is called an orbifold atlas if the following properties are satisfied:
The orbifold atlas defines the orbifold structure completely:
two orbifold atlases of X give the same orbifold structure if they can be consistently combined to give a larger orbifold atlas. Note that the orbifold structure determines the isotropy subgroup of any point of the orbifold up to isomorphism: it can be computed as the stabilizer of the point in any orbifold chart. If Ui
Uj 
Uk, then there is a unique transition element gijk in Γk such that
These transition elements satisfy
·fik = fjk·fij
as well as the cocycle relation (guaranteeing associativity)
More generally, attached to an open covering of an orbifold by orbifold charts, there is the combinatorial data of a so-called complex of groups (see below).
Exactly as in the case of manifolds, differentiability conditions can be imposed on the gluing maps to give a definition of a differentiable orbifold. It will be a Riemannian orbifold if in addition there are invariant Riemannian metrics on the orbifold charts and the gluing maps are isometries
.
For applications in geometric group theory
, it is often convenient to have a slightly more general notion of orbifold, due to Haefliger. An orbispace is to topological spaces what an orbifold is to manifolds. An orbispace is a topological generalization of the orbifold concept. It is defined by replacing the model for the orbifold charts by a locally compact space with a rigid action of a finite group, i.e. one for which points with trivial isotropy are dense. (This condition is automatically satisfied by faithful linear actions, because the points fixed by any non-trivial group element form a proper linear subspace
.) It is also useful to consider metric space
structures on an orbispace, given by invariant metric
s on the orbispace charts for which the gluing maps preserve distance. In this case each orbispace chart is usually required to be a length space with unique geodesic
s connecting any two points.
s of groupoid
s. The simplest approach (adopted by Haefliger and known also to Thurston) extends the usual notion of loop
used in the standard definition of the fundamental group
.
An orbifold path is a path in the underlying space provided with an explicit piecewise lift of path segments to orbifold charts and explicit group elements identifying paths in overlapping charts; if the underlying path is a loop, it is called an orbifold loop. Two orbifold paths are identified if they are related through multiplication by group elements in orbifold charts. The orbifold fundamental group is the group formed by homotopy classes of orbifold loops.
If the orbifold arises as the quotient of a simply connected manifold M by a proper rigid action of a discrete group Γ, the orbifold fundamental group can be identified with Γ. In general it is an extension
of Γ by π1 M.
The orbifold is said to be developable or good if it arises as the quotient by a finite group action; otherwise it is called bad. A universal covering orbifold can be constructed for an orbifold by direct analogy with the construction of the universal covering space
of a topological space, namely as the space of pairs consisting of points of the orbifold and homotopy classes of orbifold paths joining them to the basepoint. This space is naturally an orbifold.
Note that if an orbifold chart on a contractible open subset corresponds to a group Γ, then there is a natural local homomorphism of Γ into the orbifold fundamental group.
In fact the following conditions are equivalent:
, then the Birkhoff curve shortening argument can be used to prove that any orbispace path with fixed endpoints is homotopic to a unique geodesic. Applying this to constant paths in an orbispace chart, it follows that each local homomorphism is injective and hence:
Y is given by
The group elements must in addition satisfy the cocycle condition
for every chain of simplices π
ρ
σ
τ. (This condition is vacuous if Y has dimension 2 or less.)
Any choice of elements hστ in Γσ yields an equivalent complex of groups by defining
A complex of groups is called simple whenever gρστ = 1 everywhere.
It is often more convenient and conceptually appealing to pass to the barycentric subdivision
of Y. The vertices of this subdivision correspond to the simplices of Y, so that each vertex has a group attached to it. The edges of the barycentric subdivision are naturally oriented (corresponding to inclusions of simplices) and each directed edge gives an inclusion of groups. Each triangle has a transition element attached to it belonging to the group of exactly one vertex; and the tetrahedra, if there are any, give cocycle relations for the transition elements. Thus a complex of groups involves only the 3-skeleton of the barycentric subdivision; and only the 2-skeleton if it is simple.
Ui. Let Y be the abstract simplicial complex given by the nerve of the covering
: its vertices are the sets of the cover and its n-simplices correspond to non-empty intersections Uα = Ui1
··· 
Uin. For each such simplex there is an associated group Γα and the homomorphisms fij become the homomorphisms fστ. For every triple ρ 
σ 
τ corresponding to intersections
there are charts φi : Vi
Ui, φij : Vij 
Ui 
Uj and φijk : Vijk 
Ui 
Uj 
Uk and gluing maps ψ : V ij 
Vi, ψ' : V ijk 
Vij and ψ" : V ijk 
Vi.
There is a unique transition element gρστ in Γi such that gρστ·ψ" = ψ·ψ'. The relations satisfied by the transition elements of an orbifold imply those required for a complex of groups. In this way a complex of groups can be canonically associated to the nerve of an open covering by orbifold (or orbispace) charts. In the language of non-commutative sheaf theory and gerbe
s, the complex of groups in this case arises as a sheaf of groups associated to the covering Ui; the data gρστ is a 2-cocycle in non-commutative sheaf cohomology
and the data hστ gives a 2-coboundary perturbation.
j, so that there is an injection ψij : Γi 
Γj. Let Γ be the group generated by the eij and Γk with relations
for g in Γi and
if i
j 
k.
For a fixed vertex i0, the edge-path group Γ(i0) is defined to be the subgroup of Γ generated by all products
where i0, i1, ... , in, i0
is an edge-path, gk lies in Γik and eji=eij−1 if i
j.
X with finite quotient is said to be regular if it
satisfies one of the following equivalent conditions (see Bredon 1972):
The fundamental domain and quotient Y = X / Γ can naturally be identified as simplicial complexes in this case, given by the stabilisers of the simplices in the fundamental domain. A complex of groups Y is said to be developable if it arises in this way.
The action of Γ on the barycentric subdivision X ' of X always satisfies the following condition, weaker than regularity:
Indeed simplices in X ' correspond to chains of simplices in X, so that a subsimplices, given by subchains of simplices, is uniquely determined by the sizes of the simplices in the subchain. When an action satisfies this condition, then g necessarily fixes all the vertices of σ. A straightforward inductive argument shows that such an action becomes regular on the barycentric subdivision; in particular
There is in fact no need to pass to a third barycentric subdivision: as Haefliger observes using the language of category theory
, in this case the 3-skeleton of the fundamental domain of X" already carries all the necessary data – including transition elements for triangles – to define an edge-path group isomorphic to Γ.
In two dimensions this is particularly simple to describe. The fundamental domain of X" has the same structure as the barycentric subdivision Y ' of a complex of groups Y, namely:
An edge-path group can then be defined. A similar structure is inherited by the barycentric subdivision Z ' and its edge-path group is isomorphic to that of Z.
, the quotient can be given not only the structure of a complex of groups, but also that of an orbispace. This leads more generally to the definition of "orbihedron", the simplicial analogue of an orbifold.
This action of Γi on Li' extends to a simplicial action on the simplicial cone Ci over Li' (the simplicial join of i and Li'), fixing the centre i of the cone. The map φi extends to a simplicial map of
Ci onto the star
St(i) of i, carrying the centre onto i; thus φi identifies Ci / Γi, the quotient of the star of i in Ci, with St(i) and gives an orbihedron chart at i.
If i
j 
k, then there is a unique transition element gijk in Γk such that
These transition elements satisfy
·fik = fjk·fij
as well as the cocycle relation
has been to triangles of groups. This is the simplest 2-dimensional example generalising the 1-dimensional "interval of groups" discussed in Serre
's lectures on trees, where amalgamated free products
are studied in terms of actions on trees. Such triangles of groups arise any time a discrete group acts simply transitively on the triangles in the affine Bruhat-Tits building for SL3(Qp); in 1979 Mumford
discovered the first example for p = 2 (see below) as a step in producing an algebraic surface
not isomorphic to projective space
, but having the same Betti number
s. Triangles of groups were worked out in detail by Gersten and Stallings, while the more general case of complexes of groups, described above, was developed independently by Haefliger. The underlying geometric method of analysing finitely presented groups in terms of metric spaces of non-positive curvature is due to Gromov. In this context triangles of groups correspond to non-positively curved 2-dimensional simplicial complexes with the regular action of a group, transitive on triangles.
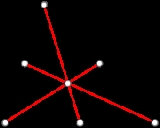
A triangle of groups is a simple complex of groups consisting of a triangle with vertices A, B, C. There are groups
There is an injective homomorphisms of ΓABC into all the other groups and of an edge group ΓXY into ΓX and ΓY. The three ways of mapping ΓABC into a vertex group all agree. (Often ΓABC is the trivial group.) The Euclidean metric structure on the corresponding orbispace is non-positively curved if and only if the link of each of the vertices in the orbihedron chart has girth at least 6.
This girth at each vertex is always even and, as observed by Stallings, can be described at a vertex A, say, as the length of the smallest word in the kernel of the natural homomorphism into ΓA of the amalgamated free product
over ΓABC of the edge groups ΓAB and ΓAC:
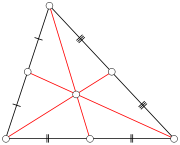
The result using the Euclidean metric structure is not optimal. Angles α, β, γ at the vertices A, B and C were defined by Stallings as 2π divided by the girth. In the Euclidean case α, β, γ ≤ π/3. However, if it is only required that α + β + γ ≤ π, it is possible to identify the
triangle with the corresponding geodesic triangle in the hyperbolic plane
with the Poincaré metric
(or the Euclidean plane if equality holds). It is a classical result from hyperbolic geometry that the hyperbolic medians intersect in the hyperbolic barycentre,
just as in the familiar Euclidean case. The barycentric subdivision and metric from this model yield a non-positively curved metric structure on the corresponding orbispace. Thus, if α+β+γ≤π,
Let α = 
be given by the binomial expansion of (1 − 8)1/2 in Q2 and set K = Q(α) 
Q2. Let
Let E = Q(ζ), a 3-dimensional vector space over K with basis 1, ζ and ζ2. Define K-linear operators on E as follows:
The elements ρ, σ and τ generate a discrete subgroup of GL3(K) which acts properly on the affine Bruhat-Tits building corresponding to SL3(Q2). This group acts transitively on all vertices, edges and triangles in the building. Let
Then
The elements σ and τ generate the stabiliser of a vertex. The link
of this vertex can be identified with the spherical building of SL3(F2) and the stabiliser can be identified with the collineation group
of the Fano plane
generated by a 3-fold symmetry σ fixing a point and a cyclic permutation τ of all 7 points, satisfying στ = τ2σ. Identifying F8* with the Fano plane, σ can be taken to be the restriction of the Frobenius automorphism σ(x) = x22 of F8 and τ to be multiplication by any element not in the prime field F2, i.e. an order 7 generator of the cyclic multiplicative group of F8. This Frobenius group acts simply transitively on the 21 flags in the Fano plane, i.e. lines with marked points. The formulas for σ and τ on E thus "lift" the formulas on F8.
Mumford also obtains an action simply transitive on the vertices of the building by passing to a subgroup of Γ1 = <ρ, σ, τ, −I>. The group Γ1 preserves the Q(α)-valued hermitian form
on Q(ζ) and can be identified with U3(f)
GL3(S) where S = Z[α,½]. Since S / (α) = F7, there is a homomorphism of the group Γ1 into GL3(F7). This action leaves invariant a
2-dimensional subspace in F73 and hence gives rise to a homomorphism Ψ of Γ1 into SL2(F7), a group of order 16·3·7. On the other hand the stabiliser of a vertex is a subgroup of order 21 and Ψ is injective on this subgroup. Thus if the congruence subgroup
Γ0 is defined as the inverse image under Ψ of the 2-Sylow subgroup of SL2(F7), the action of
Γ0 on vertices must be simply transitive.
Cartwright et al. consider actions on buildings that are simply transitive on vertices. Each such action produces a bijection (or modified duality) between the points x and lines x* in the flag complex of a finite projective plane
and a collection of oriented triangles of points (x,y,z), invariant under cyclic permutation, such that x lies on z*, y lies on x* and z lies on y* and any two points uniquely determine the third. The groups produced have generators x, labelled by points, and relations xyz = 1 for each triangle. Generically this construction will not correspond to an action on a classical affine building.
More generally, as shown by Ballmann and Brin, similar algebraic data encodes all actions that are simply transitively on the vertices of a non-positively curved 2-dimensional simplicial complex, provided the link of each vertex has girth at least 6. This data consists of:
The elements g in S label the vertices g·v in the link of a fixed vertex v; and the relations correspond to edges (g−1·v, h·v) in that link. The graph with vertices S and edges (g, h), for g−1h in S, must have girth at least 6. The original simplicial complex can be reconstructed using complexes of groups and the second barycentric subdivision.
Further examples of non-positively curved 2-dimensional complexes of groups have been constructed by Swiatkowski based on actions simply transitive on oriented edges and inducing a 3-fold symmetry on each triangle; in this case too the complex of groups is obtained from the regular action on the second barycentric subdivision. The simplest example, discovered earlier with Ballmann, starts from a finite group H with a symmetric set of generators S, not containing the identity, such that the corresponding Cayley graph
has girth at least 6. The associated group is generated by H and an involution τ subject to (τg)3 = 1 for each g in S.
In fact, if Γ acts in this way, fixing an edge (v, w), there is an involution τ interchanging v and w. The link of v is made up of vertices g·w for g in a symmetric subset S of H = Γv, generating H if the link is connected. The assumption on triangles implies that
for g in S. Thus, if σ = τg and u = g−1·w, then
By simple transitivity on the triangle (v, w, u), it follows that σ3 = 1.
The second barycentric subdivision gives a complex of groups consisting of singletons or pairs of barycentrically subdivided triangles joined along their large sides: these pairs are indexed by the quotient space S/~ obtained by identifying inverses in S. The single or "coupled" triangles are in turn joined along one common "spine". All stabilisers of simplices are trivial except for the two vertices at the ends of the spine, with stabilisers H and <τ>, and the remaining vertices of the large triangles, with stabiliser generated by an appropriate σ. Three of the smaller triangles in each large triangle contain transition elements.
When all the elements of S are involutions, none of the triangles need to be doubled. If H is taken to be the dihedral group
D7 of order 14, generated by an involution a and an element b of order 7 such that
then H is generated by the 3 involutions a, ab and ab5. The link of each vertex is given by the corresponding Cayley graph, so is just the bipartite Heawood graph
, i.e. exactly the same as in the affine building for SL3(Q2). This link structure implies that the corresponding simplicial complex is necessarily a Euclidean building. At present, however, it seems to be unknown whether any of these types of action can in fact be realised on a classical affine building: Mumford's group Γ1 (modulo scalars) is only simply transitive on edges, not on oriented edges.
A compact 2-dimensional orbifold has an Euler characteristic
Χ
given by
where Χ(X0) is the Euler characteristic of the underlying topological manifold X0, and ni are the orders of the corner reflectors, and mi are the orders of the elliptic points.
A 2-dimensional compact connected orbifold has a hyperbolic structure if its Euler characteristic is less than 0, a Euclidean structure if it is 0, and if its Euler characteristic is positive it is either bad or has an elliptic structure (an orbifold is called bad if it does not have a manifold as a covering space). In other words, its universal covering space has a hyperbolic, Euclidean, or spherical structure.
The compact 2-dimensional connected orbifolds that are not hyperbolic are listed in the table below. The 17 parabolic orbifolds are the quotients of the plane by the 17 wallpaper group
s.
Orbifold Theorem. Let M be a small 3-manifold. Let φ be a non-trivial periodic orientation-preserving diffeomorphism of M. Then M admits a φ-invariant hyperbolic or Seifert fibered structure.
This theorem is a special case of Thurston's orbifold theorem, announced without proof in 1981; it forms part of his geometrization conjecture for 3-manifolds. In particular it implies that if X is a compact, connected, orientable, irreducible, atoroidal 3-orbifold with non-empty singular locus, then M has a geometric structure (in the sense of orbifolds). A complete proof of the theorem was published by Boileau, Leeb & Porti in 2005.
, the word "orbifold" has a slightly new meaning. For mathematicians, an orbifold is a generalization of the notion of manifold
that allows the presence of the points whose neighborhood is diffeomorphic
to a quotient of Rn by a finite group, i.e. Rn/Γ. In physics, the notion of an orbifold usually describes an object that can be globally written as an orbit space M/G where M is a manifold (or a theory), and G is a group of its isometries (or symmetries) — not necessarily all of them. In string theory, these symmetries do not have to have a geometric interpretation.
A quantum field theory
defined on an orbifold becomes singular near the fixed points of G. However string theory requires us to add new parts of the closed string Hilbert space
— namely the twisted sectors where the fields defined on the closed strings are periodic up to an action from G. Orbifolding is therefore a general procedure of string theory to derive a new string theory from an old string theory in which the elements of G have been identified with the identity. Such a procedure reduces the number of states because the states must be invariant under G, but it also increases the number of states because of the extra twisted sectors. The result is usually a perfectly smooth, new string theory.
D-branes propagating on the orbifolds are described, at low energies, by gauge theories defined by the quiver diagram
s. Open strings attached to these D-branes have no twisted sector, and so the number of open string states is reduced by the orbifolding procedure.
More specifically, when the orbifold group G is a discrete subgroup of spacetime isometries, then if it has no fixed point, the result is usually a compact smooth space; the twisted sector consists of closed strings wound around the compact dimension, which are called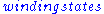
.
When the orbifold group G is a discrete subgroup of spacetime isometries, and it has fixed points, then these usually have conical singularities, because Rn/Zk
has such a singularity at the fixed point of Zk
. In string theory, gravitational singularities are usually a sign of extra degrees of freedom
which are located at locus point in spacetime. In the case of the orbifold these degrees of freedom
are the twisted states, which are strings "stuck" at the fixed points. When the fields related with these twisted states acquire a non-zero vacuum expectation value
, the singularity is deformed, i.e. the metric is changed and becomes regular at this point and around it. An example for a resulting geometry is the is Eguchi-Hanson spacetime.
From the point of view of D-branes in the vicinity of the fixed points, the effective theory of the open strings attached to these D-branes is a supersymmetric field theory, whose space of vacua has a singular point, where additional massless degrees of freedom exist. The fields related with the closed string twisted sector couple to the open strings in such a way as to add a Fayet-Iliopoulos term to the supersymmetric field theory Lagrangian, so that when such a field acquires a non-zero vacuum expectation value
, the Fayet-Iliopoulos term is non-zero, and thereby deforms the theory (i.e. changes it) so that the singularity no longer exists http://arxiv.org/abs/hep-th/9603167, http://www-spires.fnal.gov/spires/find/hep/www?j=NUPHA,B342,246.
,
the construction of realistic phenomenological models requires dimensional reduction
because the strings naturally propagate in a 10-dimensional space whilst the observed dimension of space-time of the universe is 4. Formal constraints on the theories nevertheless place restrictions on the compactified space
in which the extra "hidden" variables live: when looking for realistic 4-dimensional models with supersymmetry
, the auxiliary compactified space must be a 6-dimensional Calabi-Yau manifold
.
There are a large number of possible Calabi-Yau manifolds (tens of thousands), whence the use of the term "swampland" in the current theoretical physics literature to describe the baffling choice. The general study of Calabi-Yau manifolds is mathematically complex and for a long time examples have been hard to construct explicitly. Orbifolds have therefore proved very useful since they automatically satisfy the constraints imposed by supersymmetry. They provide degenerate examples of Calabi-Yau manifolds due to their singular points, but this is completely acceptable from the point of view of theoretical physics. Such orbifolds are called "supersymmetric": they are technically easier to study than general Calabi-Yau manifolds. It is very often possible to associate a continuous family of non-singular Calabi-Yau manifolds to a singular supersymmetric orbifold. In 4 dimensions this can be illustrated using complex K3 surface
s:
The study of Calabi-Yau manifolds in string theory and the duality between different models of string theory (type IIA and IIB) led to the idea of mirror symmetry in 1988. The role of orbifolds was first pointed out by Dixon, Harvey, Vafa and Witten around the same time.
in the work of Dmitri Tymoczko
and collaborators and . This is considered a sophisticated application of mathematics to music theory, with the resulting paper being the first music theory paper published by Science
.
Tymoczko models musical chords consisting of n notes, not necessarily distinct, as points in the orbifold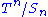
– the space of n unordered points (not necessarily distinct) in the circle, realized as the quotient of the n-torus
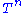(the space of n ordered points on the circle) by the symmetric group 
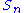(corresponding from moving from an ordered set to an unordered set).
Musically, this is explained as follows:
For dyad
s (two tones), this yields the closed Möbius strip
; for triad
s (three tones), this yields an orbifold that can be described as a triangular prism with the top and bottom triangular faces identified with a 120° twist (a ⅓ twist) – equivalently, as a solid torus in 3 dimensions with a cross-section an equilateral triangle and such a twist.
The resulting orbifold is naturally stratified by repeated tones (properly, by integer partitions of t) – the open set consists of distinct tones (the partition
), while there is a 1-dimensional singular set consisting of all tones being the same (the partition 
), which topologically is a circle, and various intermediate partitions. There is also a notable circle which runs through the center of the open set consisting of equally spaced points. In the case of triads, the three side faces of the prism correspond to two tones being the same and the third different (the partition 
), while the three edges of the prism correspond to the 1-dimensional singular set. The top and bottom faces are part of the open set, and only appear because the orbifold has been cut – if viewed as a triangular torus with a twist, these artifacts disappear.
Tymoczko argues that chords close to the center (with tones equally or almost equally spaced) form the basis of much of traditional Western harmony, and that visualizing them in this way assists in analysis. There are 4 chords on the center (equally spaced under equal temperament
– spacing of 4/4/4 between tones), corresponding to the augmented triad
s (thought of as musical sets
) C♯FA, DF♯A♯, D♯GB, and EG♯C (then they cycle: FAC♯ = C♯FA), with the 12 major chord
s and 12 minor chord
s being the points next to but not on the center – almost evenly spaced but not quite. Major chords correspond to 4/3/5 (or equivalently, 5/4/3) spacing, while minor chords correspond to 3/4/5 spacing. Key changes then correspond to movement between these points in the orbifold, with smoother changes effected by movement between nearby points.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, an orbifold (for "orbit-manifold") is a generalization of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. It is a topological space (called the underlying space) with an orbifold structure (see below).
The underlying space locally looks like the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of a
Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
under the linear action of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
.
Definitions of orbifold have been given several times: by Satake
Ichirô Satake
Ichirô Satake is a mathematician who introduced the Satake isomorphism.-External links:* from Oberwolfach...
in the context of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s in the 1950s under the name V-manifold; by Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
in the context of the geometry of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s in the 1970s when he coined the name orbifold, after a vote by his students; and by Haefliger
André Haefliger
André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...
in the 1980s in the context of Gromov's programme on CAT(k) space
CAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
s under the name orbihedron. The definition of Thurston will be described here: it is the most widely used and is applicable in all cases.
Mathematically, orbifolds arose first as surfaces with singular points long before they were formally defined. One of the first classical examples arose in the theory of modular forms with the action of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
SL(2,Z) on the upper half-plane: a version of the Riemann–Roch theorem holds after the quotient is compactified by the addition of two orbifold cusp points. In 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
theory, the theory of Seifert fiber spaces, initiated by Seifert
Herbert Seifert
Herbert Karl Johannes Seifert was a German mathematician known for his work in topology....
, can be phrased in terms of 2-dimensional orbifolds. In geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, post-Gromov, discrete groups have been studied in terms of the local curvature properties of orbihedra and their covering spaces.
In string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the word "orbifold" has a slightly different meaning, discussed in detail below. In conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
, a mathematical part of string theory, it is often used to refer to the theory attached to the fixed point subalgebra of a vertex algebra under the action of a finite group of automorphisms.
The main example of underlying space is a quotient space of a manifold under the properly discontinuous
Properly discontinuous
In topology and related branches of mathematics, an action of a group G on a topological space X is called proper if the map from G×X to X×X taking to is proper, and is called properly discontinuous if in addition G is discrete...
action of a possibly infinite group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s with finite isotropy subgroups. In particular this applies to any action of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
; thus a manifold with boundary carries a natural orbifold structure, since it is the quotient of its double by an action of Z2.
Similarly the quotient space of a manifold by a smooth proper action of S1 carries the structure of an orbifold.
Orbifold structure gives a natural stratification
Stratification (mathematics)
-In mathematical logic:In mathematical logic, stratification is any consistent assignment of numbers to predicate symbols guaranteeing that a unique formal interpretation of a logical theory exists...
by open manifolds on its underlying space, where one stratum corresponds to a set of singular points of the same type.
It should be noted that one topological space can carry many different orbifold structures.
For example, consider the orbifold O associated with a factor space of the 2-sphere along a rotation by
; it is homeomorphic to the 2-sphere, but the natural orbifold structure is different.It is possible to adopt most of the characteristics of manifolds to orbifolds and these characteristics are usually different from correspondent characteristics of underlying space.
In the above example, the orbifold fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of O is Z2
and its orbifold Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
is 1.
Formal definitions
Like a manifold, an orbifold is specified by local conditions; however, instead of being locally modelled on open subsets of Rn, an orbifold is locally modelled on quotients of open subsets of Rn by finite group actions. The structure of an orbifold encodes not only that of the underlying quotient space, which need not be a manifold, but also that of the isotropy subgroups.An n-dimensional orbifold is a Hausdorff topological space X, called the underlying space, with a covering by a collection of open sets Ui, closed under finite intersection. For each Ui, there is
- an open subset Vi of Rn, invariant under a faithful linear action of a finite group Γi
- a continuous map φi of Vi onto Ui invariant under Γi, called an orbifold chart, which defines a homeomorphism between Vi / Γi and Ui.
The collection of orbifold charts is called an orbifold atlas if the following properties are satisfied:
- for each inclusion Ui
Uj there is an injective group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
fij : Γi
Γj - for each inclusion Ui
Uj there is a Γi -equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
homeomorphism ψij, called a gluing map, of Vi onto an open subset of Vj - the gluing maps are compatible with the charts, i.e. φj·ψij = φi
- the gluing maps are unique up to composition with group elements, i.e. any other possible gluing map from Vi to Vj has the form g·ψij for a unique g in Γj
The orbifold atlas defines the orbifold structure completely:
two orbifold atlases of X give the same orbifold structure if they can be consistently combined to give a larger orbifold atlas. Note that the orbifold structure determines the isotropy subgroup of any point of the orbifold up to isomorphism: it can be computed as the stabilizer of the point in any orbifold chart. If Ui
Uj Uk, then there is a unique transition element gijk in Γk such that- gijk·ψik = ψjk·ψij
These transition elements satisfy
·fik = fjk·fij
as well as the cocycle relation (guaranteeing associativity)
- fkm(gijk)·gikm = gijm·gjkm.
More generally, attached to an open covering of an orbifold by orbifold charts, there is the combinatorial data of a so-called complex of groups (see below).
Exactly as in the case of manifolds, differentiability conditions can be imposed on the gluing maps to give a definition of a differentiable orbifold. It will be a Riemannian orbifold if in addition there are invariant Riemannian metrics on the orbifold charts and the gluing maps are isometries
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
.
For applications in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, it is often convenient to have a slightly more general notion of orbifold, due to Haefliger. An orbispace is to topological spaces what an orbifold is to manifolds. An orbispace is a topological generalization of the orbifold concept. It is defined by replacing the model for the orbifold charts by a locally compact space with a rigid action of a finite group, i.e. one for which points with trivial isotropy are dense. (This condition is automatically satisfied by faithful linear actions, because the points fixed by any non-trivial group element form a proper linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
.) It is also useful to consider metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
structures on an orbispace, given by invariant metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s on the orbispace charts for which the gluing maps preserve distance. In this case each orbispace chart is usually required to be a length space with unique geodesic
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
s connecting any two points.
Examples
- Any manifold without boundary is trivially an orbifold. Each of the groups Γi is the trivial groupTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
.
- If N is a compact manifold with boundary, its double M can formed by gluing together a copy of N and its mirror image along their common boundary. There is natural reflection action of Z2 on the manifold M fixing the common boundary; the quotient space can be identified with N, so that N has a natural orbifold structure.
- If M is a Riemannian n-manifold with a cocompact properProper mapIn mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
isometric action of a discrete group Γ, then the orbit space X = M/Γ has natural orbifold structure: for each x in X take a representative m in M and an open neighbourhood Vm of m invariant under the stabiliser Γm, identified equivariantly with a Γm-subset of TmM under the exponential map at m; finitely many neighbourhoods cover X and each of their finite intersections, if non-empty, is covered by an intersection of Γ-translates gm·Vm with corresponding group gm Γ gm−1. Orbifolds that arise in this way are called developable or good.
- A classical theorem of Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
constructs Fuchsian groupFuchsian groupIn mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s as hyperbolic reflection groupReflection groupIn group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
s generated by reflections in the edges of a geodesic triangle in the hyperbolic planeHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
for the Poincaré metricPoincaré metricIn mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
. If the triangle has angles π / ni for positive integers ni, the triangle is a fundamental domainFundamental domainIn geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
and naturally a 2-dimensional orbifold. The corresponding group is an example of a hyperbolic triangle groupTriangle groupIn mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
. Poincaré also gave a 3-dimensional version of this result for Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s: in this case the Kleinian group Γ is generated by hyperbolic reflections and the orbifold is H3 / Γ.
- If M is a closed 2-manifold, new orbifold structures can be defined on Mi by removing finitely many disjoint closed discs from M and gluing back copies of discs D/ Γi where D is the closed unit disc and Γi is a finite cyclic group of rotations. This generalises Poincaré's construction.
Orbifold fundamental group
There are several ways to define the orbifold fundamental group. More sophisticated approaches use orbifold covering spaces or classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
s of groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s. The simplest approach (adopted by Haefliger and known also to Thurston) extends the usual notion of loop
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
used in the standard definition of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
.
An orbifold path is a path in the underlying space provided with an explicit piecewise lift of path segments to orbifold charts and explicit group elements identifying paths in overlapping charts; if the underlying path is a loop, it is called an orbifold loop. Two orbifold paths are identified if they are related through multiplication by group elements in orbifold charts. The orbifold fundamental group is the group formed by homotopy classes of orbifold loops.
If the orbifold arises as the quotient of a simply connected manifold M by a proper rigid action of a discrete group Γ, the orbifold fundamental group can be identified with Γ. In general it is an extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of Γ by π1 M.
The orbifold is said to be developable or good if it arises as the quotient by a finite group action; otherwise it is called bad. A universal covering orbifold can be constructed for an orbifold by direct analogy with the construction of the universal covering space
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a topological space, namely as the space of pairs consisting of points of the orbifold and homotopy classes of orbifold paths joining them to the basepoint. This space is naturally an orbifold.
Note that if an orbifold chart on a contractible open subset corresponds to a group Γ, then there is a natural local homomorphism of Γ into the orbifold fundamental group.
In fact the following conditions are equivalent:
- The orbifold is developable.
- The orbifold structure on the universal covering orbifold is trivial.
- The local homomorphisms are all injective for a covering by contractible open sets.
Non-positively curved orbispaces
As explained above, an orbispace is basically a generalization of the orbifold concept applied to topological spaces. Let then X be an orbispace endowed with a metric space structure for which the charts are geodesic length spaces. The preceding definitions and results for orbifolds can be generalized to give definitions of orbispace fundamental group and universal covering orbispace, with analogous criteria for developability. The distance functions on the orbispace charts can be used to define the length of an orbispace path in the universal covering orbispace. If the distance function in each chart is non-positively curvedCAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
, then the Birkhoff curve shortening argument can be used to prove that any orbispace path with fixed endpoints is homotopic to a unique geodesic. Applying this to constant paths in an orbispace chart, it follows that each local homomorphism is injective and hence:
- every non-positively curved orbispace is developable (i.e. good).
Complexes of groups
Every orbifold has associated with it an additional combinatorial structure given by a complex of groups.Definition
A complex of groups (Y,f,g) on an abstract simplicial complexAbstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
Y is given by
- a finite group Γσ for each simplex σ of Y
- an injective homomorphism fστ : Γτ
Γσ whenever σ 
τ - for every inclusion ρ
σ 
τ, a group element gρστ in Γρ such that (Ad gρστ)·fρτ = fρσ·fστ (here Ad denotes the adjoint action by conjugation)
The group elements must in addition satisfy the cocycle condition
- fπρ(gρστ) gπρτ = gπστ gπρσ
for every chain of simplices π
ρ σ τ. (This condition is vacuous if Y has dimension 2 or less.)Any choice of elements hστ in Γσ yields an equivalent complex of groups by defining
- fστ = (Ad hστ)·fστ
- gρστ = hρσ·fρσ(hστ)·gρστ·hρτ−1
A complex of groups is called simple whenever gρστ = 1 everywhere.
- An easy inductive argument shows that every complex of groups on a simplex is equivalent to a complex of groups with gρστ = 1 everywhere.
It is often more convenient and conceptually appealing to pass to the barycentric subdivision
Barycentric subdivision
In geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.The name...
of Y. The vertices of this subdivision correspond to the simplices of Y, so that each vertex has a group attached to it. The edges of the barycentric subdivision are naturally oriented (corresponding to inclusions of simplices) and each directed edge gives an inclusion of groups. Each triangle has a transition element attached to it belonging to the group of exactly one vertex; and the tetrahedra, if there are any, give cocycle relations for the transition elements. Thus a complex of groups involves only the 3-skeleton of the barycentric subdivision; and only the 2-skeleton if it is simple.
Example
If X is an orbifold (or orbispace), choose a covering by open subsets from amongst the orbifold charts fi : Vi Ui. Let Y be the abstract simplicial complex given by the nerve of the coveringNerve of an open covering
In mathematics, the nerve of an open covering is a construction in topology, of an abstract simplicial complex from an open covering of a topological space X.The notion of nerve was introduced by Pavel Alexandrov....
: its vertices are the sets of the cover and its n-simplices correspond to non-empty intersections Uα = Ui1
··· Uin. For each such simplex there is an associated group Γα and the homomorphisms fij become the homomorphisms fστ. For every triple ρ σ τ corresponding to intersections- Ui
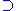Ui 
Uj 
Ui 
Uj 
Uk
there are charts φi : Vi
Ui, φij : Vij Ui Uj and φijk : Vijk Ui Uj Uk and gluing maps ψ : V ij Vi, ψ' : V ijk Vij and ψ" : V ijk Vi.There is a unique transition element gρστ in Γi such that gρστ·ψ" = ψ·ψ'. The relations satisfied by the transition elements of an orbifold imply those required for a complex of groups. In this way a complex of groups can be canonically associated to the nerve of an open covering by orbifold (or orbispace) charts. In the language of non-commutative sheaf theory and gerbe
Gerbe
In mathematics, a gerbe is a construct in homological algebra and topology. Gerbes were introduced by Jean Giraud following ideas of Alexandre Grothendieck as a tool for non-commutative cohomology in degree 2. They can be seen as a generalization of principal bundles to the setting of 2-categories...
s, the complex of groups in this case arises as a sheaf of groups associated to the covering Ui; the data gρστ is a 2-cocycle in non-commutative sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
and the data hστ gives a 2-coboundary perturbation.
Edge-path group
The edge-path group of a complex of groups can be defined as a natural generalisation of the edge path group of a simplicial complex. In the barycentric subdivision of Y, take generators eij corresponding to edges from i to j where i j, so that there is an injection ψij : Γi Γj. Let Γ be the group generated by the eij and Γk with relations- eij –1 · g · eij = ψij(g)
for g in Γi and
- eik = ejk·eij·gijk
if i
j k.For a fixed vertex i0, the edge-path group Γ(i0) is defined to be the subgroup of Γ generated by all products
- g0 · ei0 i1 · g1 · ei1 i2 · ··· · gn · eini 0
where i0, i1, ... , in, i0
is an edge-path, gk lies in Γik and eji=eij−1 if i
j.Developable complexes
A simplicial proper action of a discrete group Γ on a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
X with finite quotient is said to be regular if it
satisfies one of the following equivalent conditions (see Bredon 1972):
- X admits a finite subcomplex as fundamental domainFundamental domainIn geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
;
- the quotient Y = X/Γ has a natural simplicial structure;
- the quotient simplicial structure on orbit-representatives of vertices is consistent;
- if (v0, ... , vk) and (g0·v0, ... , gk·vk) are simplices, then g·vi = gi·vi for some g in Γ.
The fundamental domain and quotient Y = X / Γ can naturally be identified as simplicial complexes in this case, given by the stabilisers of the simplices in the fundamental domain. A complex of groups Y is said to be developable if it arises in this way.
- A complex of groups is developable if and only if the homomorphisms of Γσ into the edge-path group are injective.
- A complex of groups is developable if and only if for each simplex σ there is an injective homomorphism θσ from Γσ into a fixed discrete group Γ such that θτ·fστ = θσ. In ths case the simplicial complex X is canonically defined: it has k-simplices (σ, xΓσ) where σ is a k-simplex of Y and x runs over Γ / Γσ. Consistency can be checked using the fact that the restriction of the complex of groups to a simplex is equivalent to one with trivial cocycle gρστ.
The action of Γ on the barycentric subdivision X ' of X always satisfies the following condition, weaker than regularity:
- whenever σ and g·σ are subsimplices of some simplex τ, they are equal, i.e. σ = g·σ
Indeed simplices in X ' correspond to chains of simplices in X, so that a subsimplices, given by subchains of simplices, is uniquely determined by the sizes of the simplices in the subchain. When an action satisfies this condition, then g necessarily fixes all the vertices of σ. A straightforward inductive argument shows that such an action becomes regular on the barycentric subdivision; in particular
- the action on the second barycentric subdivision X" is regular;
- Γ is naturally isomorphic to the edge-path group defined using edge-paths and vertex stabilisers for the barycentric subdivison of the fundamental domain in X".
There is in fact no need to pass to a third barycentric subdivision: as Haefliger observes using the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, in this case the 3-skeleton of the fundamental domain of X" already carries all the necessary data – including transition elements for triangles – to define an edge-path group isomorphic to Γ.
In two dimensions this is particularly simple to describe. The fundamental domain of X" has the same structure as the barycentric subdivision Y ' of a complex of groups Y, namely:
- a finite 2-dimensional simplicial complex Z;
- an orientation for all edges i
j; - if i
j and j 
k are edges, then i 
k is an edge and (i, j, k) is a triangle; - finite groups attached to vertices, inclusions to edges and transition elements, describing compatibility, to triangles.
An edge-path group can then be defined. A similar structure is inherited by the barycentric subdivision Z ' and its edge-path group is isomorphic to that of Z.
Orbihedra
If a countable discrete group acts by a regular simplicial proper action on a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
, the quotient can be given not only the structure of a complex of groups, but also that of an orbispace. This leads more generally to the definition of "orbihedron", the simplicial analogue of an orbifold.
Definition
Let X be a finite simplicial complex with barycentric subdivision X '. An orbihedron structure consists of:- for each vertex i of X ', a simplicial complex Li' endowed with a rigid simplicial action of a finite group Γi.
- a simplicial map φi of Li' onto the link Li of i in X ', identifying the quotient Li' / Γi with Li.
This action of Γi on Li' extends to a simplicial action on the simplicial cone Ci over Li' (the simplicial join of i and Li'), fixing the centre i of the cone. The map φi extends to a simplicial map of
Ci onto the star
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
St(i) of i, carrying the centre onto i; thus φi identifies Ci / Γi, the quotient of the star of i in Ci, with St(i) and gives an orbihedron chart at i.
- for each directed edge i
j of X ', an injective homomorphism fij of Γi into Γj. - for each directed edge i
j, a Γi equivariant simplicial gluing map ψij of Ci into Cj. - the gluing maps are compatible with the charts, i.e. φj·ψij = φi.
- the gluing maps are unique up to composition with group elements, i.e. any other possible gluing map from Vi to Vj has the form g·ψij for a unique g in Γj.
If i
j k, then there is a unique transition element gijk in Γk such that- gijk·ψik = ψjk·ψij
These transition elements satisfy
·fik = fjk·fij
as well as the cocycle relation
- ψkm(gijk)·gikm = gijm·gjkm.
Main properties
- The group theoretic data of an orbihedron gives a complex of groups on X, because the vertices i of X ' correspond to the simplices in X.
- Every complex of groups on X is associated with an essentially unique orbihedron structure on X. This key fact follows by noting that the star and link of a vertex i of X ', corresponding to a simplex σ of X, have natural decompositions: the star is isomorphic to the abstract simplicial complex given by the join of σ and the barycentric subdivision σ' of σ; and the link is isomorphic to join of the link of σ in X and the link of the barycentre of σ in σ'. Restricting the complex of groups to the link of σ in X, all the groups Γτ come with injective homomorphisms into Γσ. Since the link of i in X ' is canonically covered by a simplicial complex on which Γσ acts, this defines an orbihedron structure on X.
- The orbihedron fundamental group is (tautologically) just the edge-path group of the associated complex of groups.
- Every orbihedron is also naturally an orbispace: indeed in the geometric realization of the simplicial complex, orbispace charts can be defined using the interiors of stars.
- The orbihedron fundamental group can be naturally identified with the orbispace fundamental group of the associated orbispace. This follows by applying the simplicial approximation theoremSimplicial approximation theoremIn mathematics, the simplicial approximation theorem is a foundational result for algebraic topology, guaranteeing that continuous mappings can be approximated by ones that are piecewise of the simplest kind. It applies to mappings between spaces that are built up from simplices — that is,...
to segments of an orbispace path lying in an orbispace chart: it is a straightforward variant of the classical proof that the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a polyhedron can be identified with its edge-path group.
- The orbispace associated to an orbihedron has a canonical metric structure, coming locally from the length metric in the standard geometric realization in Euclidean space, with vertices mapped to an orthonormal basis. Other metric structures are also used, involving length metrics obtained by realizing the simplices in hyperbolic spaceHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, with simplices identified isometrically along common boundaries.
- The orbispace associated to an orbihedron is non-positively curved if and only if the link in each orbihedron chart has girth greater than or equal to 6, i.e. any closed circuit in the link has length at least 6. This condition, well known from the theory of Hadamard spacesCAT(k) spaceIn mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
, depends only on the underlying complex of groups.
- When the universal covering orbihedron is non-positively curved the fundamental group is infinite and is generated by isomorphic copies of the isotropy groups. This follows from the corresponding result for orbispaces.
Triangles of groups
Historically one of the most important applications of orbifolds in geometric group theoryGeometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
has been to triangles of groups. This is the simplest 2-dimensional example generalising the 1-dimensional "interval of groups" discussed in Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
's lectures on trees, where amalgamated free products
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
are studied in terms of actions on trees. Such triangles of groups arise any time a discrete group acts simply transitively on the triangles in the affine Bruhat-Tits building for SL3(Qp); in 1979 Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
discovered the first example for p = 2 (see below) as a step in producing an algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
not isomorphic to projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, but having the same Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s. Triangles of groups were worked out in detail by Gersten and Stallings, while the more general case of complexes of groups, described above, was developed independently by Haefliger. The underlying geometric method of analysing finitely presented groups in terms of metric spaces of non-positive curvature is due to Gromov. In this context triangles of groups correspond to non-positively curved 2-dimensional simplicial complexes with the regular action of a group, transitive on triangles.
A triangle of groups is a simple complex of groups consisting of a triangle with vertices A, B, C. There are groups
- ΓA, ΓB, ΓC at each vertex
- ΓBC, ΓCA, ΓAB for each edge
- ΓABC for the triangle itself.
There is an injective homomorphisms of ΓABC into all the other groups and of an edge group ΓXY into ΓX and ΓY. The three ways of mapping ΓABC into a vertex group all agree. (Often ΓABC is the trivial group.) The Euclidean metric structure on the corresponding orbispace is non-positively curved if and only if the link of each of the vertices in the orbihedron chart has girth at least 6.
This girth at each vertex is always even and, as observed by Stallings, can be described at a vertex A, say, as the length of the smallest word in the kernel of the natural homomorphism into ΓA of the amalgamated free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
over ΓABC of the edge groups ΓAB and ΓAC:
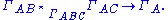
The result using the Euclidean metric structure is not optimal. Angles α, β, γ at the vertices A, B and C were defined by Stallings as 2π divided by the girth. In the Euclidean case α, β, γ ≤ π/3. However, if it is only required that α + β + γ ≤ π, it is possible to identify the
triangle with the corresponding geodesic triangle in the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
with the Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
(or the Euclidean plane if equality holds). It is a classical result from hyperbolic geometry that the hyperbolic medians intersect in the hyperbolic barycentre,
just as in the familiar Euclidean case. The barycentric subdivision and metric from this model yield a non-positively curved metric structure on the corresponding orbispace. Thus, if α+β+γ≤π,
- the orbispace of the triangle of groups is developable;
- the corresponding edge-path group, which can also be described as the colimit of the triangle of groups, is infinite;
- the homomorphisms of the vertex groups into the edge-path group are injections.
Mumford's example
be given by the binomial expansion of (1 − 8)1/2 in Q2 and set K = Q(α) Q2. Let- ζ = exp 2πi/7
- λ = (α − 1)/2 = ζ + ζ2 + ζ4
- μ = λ/λ*.
Let E = Q(ζ), a 3-dimensional vector space over K with basis 1, ζ and ζ2. Define K-linear operators on E as follows:
- σ is the generator of the Galois groupGalois groupIn mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of E over K, an element of order 3 given by σ(ζ) = ζ2 - τ is the operator of multiplication by ζ on E, an element of order 7
- ρ is the operator given by ρ(ζ) = 1, ρ(ζ2) = ζ and ρ(1) = μ·ζ2, so that ρ3 is scalar multiplication by μ.
The elements ρ, σ and τ generate a discrete subgroup of GL3(K) which acts properly on the affine Bruhat-Tits building corresponding to SL3(Q2). This group acts transitively on all vertices, edges and triangles in the building. Let
- σ1 = σ, σ2 = ρσρ−1, σ3 = ρ2σρ−2.
Then
- σ1, σ2 and σ3 generate a subgroup Γ of SL3(K).
- Γ is the smallest subgroup generated by σ and τ, invariant under conjugation by ρ.
- Γ acts simply transitively on the triangles in the building.
- There is a triangle Δ such that the stabiliser of its edges are the subgroups of order 3 generated by the σi's.
- The stabiliser of a vertices of Δ is the Frobenius groupFrobenius groupIn mathematics, a Frobenius group is a transitive permutation group on a finite set, such that no non-trivial elementfixes more than one point and some non-trivial element fixes a point.They are named after F. G. Frobenius.- Structure :...
of order 21 generated by the two order 3 elements stabilising the edges meeting at the vertex. - The stabiliser of Δ is trivial.
The elements σ and τ generate the stabiliser of a vertex. The link
Link (graph theory)
In geometry, the link of a vertex of a 2-dimensional simplicial complex is a graph that encodes information about the local structure of the complex at the vertex.It is a graph-theoretic analog to a sphere centered at a point.- Example :...
of this vertex can be identified with the spherical building of SL3(F2) and the stabiliser can be identified with the collineation group
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
of the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
generated by a 3-fold symmetry σ fixing a point and a cyclic permutation τ of all 7 points, satisfying στ = τ2σ. Identifying F8* with the Fano plane, σ can be taken to be the restriction of the Frobenius automorphism σ(x) = x22 of F8 and τ to be multiplication by any element not in the prime field F2, i.e. an order 7 generator of the cyclic multiplicative group of F8. This Frobenius group acts simply transitively on the 21 flags in the Fano plane, i.e. lines with marked points. The formulas for σ and τ on E thus "lift" the formulas on F8.
Mumford also obtains an action simply transitive on the vertices of the building by passing to a subgroup of Γ1 = <ρ, σ, τ, −I>. The group Γ1 preserves the Q(α)-valued hermitian form
- f(x,y)=xy* + σ(xy*) + σ2(xy*)
on Q(ζ) and can be identified with U3(f)
GL3(S) where S = Z[α,½]. Since S / (α) = F7, there is a homomorphism of the group Γ1 into GL3(F7). This action leaves invariant a2-dimensional subspace in F73 and hence gives rise to a homomorphism Ψ of Γ1 into SL2(F7), a group of order 16·3·7. On the other hand the stabiliser of a vertex is a subgroup of order 21 and Ψ is injective on this subgroup. Thus if the congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
Γ0 is defined as the inverse image under Ψ of the 2-Sylow subgroup of SL2(F7), the action of
Γ0 on vertices must be simply transitive.
Generalizations
Other examples of triangles or 2-dimensional complexes of groups can be constructed by variations of the above example.Cartwright et al. consider actions on buildings that are simply transitive on vertices. Each such action produces a bijection (or modified duality) between the points x and lines x* in the flag complex of a finite projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
and a collection of oriented triangles of points (x,y,z), invariant under cyclic permutation, such that x lies on z*, y lies on x* and z lies on y* and any two points uniquely determine the third. The groups produced have generators x, labelled by points, and relations xyz = 1 for each triangle. Generically this construction will not correspond to an action on a classical affine building.
More generally, as shown by Ballmann and Brin, similar algebraic data encodes all actions that are simply transitively on the vertices of a non-positively curved 2-dimensional simplicial complex, provided the link of each vertex has girth at least 6. This data consists of:
- a generating set S containing inverses, but not the identity;
- a set of relations g h k = 1, invariant under cyclic permutation.
The elements g in S label the vertices g·v in the link of a fixed vertex v; and the relations correspond to edges (g−1·v, h·v) in that link. The graph with vertices S and edges (g, h), for g−1h in S, must have girth at least 6. The original simplicial complex can be reconstructed using complexes of groups and the second barycentric subdivision.
Further examples of non-positively curved 2-dimensional complexes of groups have been constructed by Swiatkowski based on actions simply transitive on oriented edges and inducing a 3-fold symmetry on each triangle; in this case too the complex of groups is obtained from the regular action on the second barycentric subdivision. The simplest example, discovered earlier with Ballmann, starts from a finite group H with a symmetric set of generators S, not containing the identity, such that the corresponding Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
has girth at least 6. The associated group is generated by H and an involution τ subject to (τg)3 = 1 for each g in S.
In fact, if Γ acts in this way, fixing an edge (v, w), there is an involution τ interchanging v and w. The link of v is made up of vertices g·w for g in a symmetric subset S of H = Γv, generating H if the link is connected. The assumption on triangles implies that
- τ·(g·w) = g−1·w
for g in S. Thus, if σ = τg and u = g−1·w, then
- σ(v) = w, σ(w) = u, σ(u) = w.
By simple transitivity on the triangle (v, w, u), it follows that σ3 = 1.
The second barycentric subdivision gives a complex of groups consisting of singletons or pairs of barycentrically subdivided triangles joined along their large sides: these pairs are indexed by the quotient space S/~ obtained by identifying inverses in S. The single or "coupled" triangles are in turn joined along one common "spine". All stabilisers of simplices are trivial except for the two vertices at the ends of the spine, with stabilisers H and <τ>, and the remaining vertices of the large triangles, with stabiliser generated by an appropriate σ. Three of the smaller triangles in each large triangle contain transition elements.
When all the elements of S are involutions, none of the triangles need to be doubled. If H is taken to be the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D7 of order 14, generated by an involution a and an element b of order 7 such that
- ab= b−1a,
then H is generated by the 3 involutions a, ab and ab5. The link of each vertex is given by the corresponding Cayley graph, so is just the bipartite Heawood graph
Heawood graph
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
, i.e. exactly the same as in the affine building for SL3(Q2). This link structure implies that the corresponding simplicial complex is necessarily a Euclidean building. At present, however, it seems to be unknown whether any of these types of action can in fact be realised on a classical affine building: Mumford's group Γ1 (modulo scalars) is only simply transitive on edges, not on oriented edges.
2-dimensional orbifolds
In two dimensions, there are three singular point types of an orbifold:- A boundary point
- An elliptic point of order n, such as the origin of R2 quotiented out by a cyclic group of order n of rotations.
- A corner reflector of order n: the origin of R2 quotiented out by a dihedral group of order 2n.
A compact 2-dimensional orbifold has an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
Χ
given by
- Χ = Χ(X0) − Σ(1 − 1/ni )/2 − Σ(1 − 1/mi )
where Χ(X0) is the Euler characteristic of the underlying topological manifold X0, and ni are the orders of the corner reflectors, and mi are the orders of the elliptic points.
A 2-dimensional compact connected orbifold has a hyperbolic structure if its Euler characteristic is less than 0, a Euclidean structure if it is 0, and if its Euler characteristic is positive it is either bad or has an elliptic structure (an orbifold is called bad if it does not have a manifold as a covering space). In other words, its universal covering space has a hyperbolic, Euclidean, or spherical structure.
The compact 2-dimensional connected orbifolds that are not hyperbolic are listed in the table below. The 17 parabolic orbifolds are the quotients of the plane by the 17 wallpaper group
Wallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s.
| Type | Euler characteristic | Underlying 2-manifold | Orders of elliptic points | Orders of corner reflectors |
|---|---|---|---|---|
| Bad | 1 + 1/n | Sphere | n > 1 | |
| Bad | 1/m + 1/n | Sphere | n > m > 1 | |
| Bad | 1/2 + 1/2n | Disk | n > 1 | |
| Bad | 1/2m + 1/2n | Disk | n > m > 1 | |
| Elliptic | 2 | Sphere | ||
| Elliptic | 2/n | Sphere | n,n | |
| Elliptic | 1/n | Sphere | 2, 2, n | |
| Elliptic | 1/6 | Sphere | 2, 3, 3 | |
| Elliptic | 1/12 | Sphere | 2, 3, 4 | |
| Elliptic | 1/30 | Sphere | 2, 3, 5 | |
| Elliptic | 1 | Disc | ||
| Elliptic | 1/n | Disc | n, n | |
| Elliptic | 1/2n | Disc | 2, 2, n | |
| Elliptic | 1/12 | Disc | 2, 3, 3 | |
| Elliptic | 1/24 | Disc | 2, 3, 4 | |
| Elliptic | 1/60 | Disc | 2, 3, 5 | |
| Elliptic | 1/n | Disc | n | |
| Elliptic | 1/2n | Disc | 2 | n |
| Elliptic | 1/12 | Disc | 3 | 2 |
| Elliptic | 1 | Projective plane | ||
| Elliptic | 1/n | Projective plane | n | |
| Parabolic | 0 | Sphere | 2, 3, 6 | |
| Parabolic | 0 | Sphere | 2, 4, 4 | |
| Parabolic | 0 | Sphere | 3, 3, 3 | |
| Parabolic | 0 | Sphere | 2, 2, 2, 2 | |
| Parabolic | 0 | Disk | 2, 3, 6 | |
| Parabolic | 0 | Disk | 2, 4, 4 | |
| Parabolic | 0 | Disk | 3, 3, 3 | |
| Parabolic | 0 | Disk | 2, 2, 2, 2 | |
| Parabolic | 0 | Disk | 2 | 2, 2 |
| Parabolic | 0 | Disk | 3 | 3 |
| Parabolic | 0 | Disk | 4 | 2 |
| Parabolic | 0 | Disk | 2, 2 | |
| Parabolic | 0 | Projective plane | 2, 2 | |
| Parabolic | 0 | Torus | ||
| Parabolic | 0 | Klein bottle | ||
| Parabolic | 0 | Annulus | ||
| Parabolic | 0 | Moebius band |
3-dimensional orbifolds
A 3-manifold is said to be small if it is closed, irreducible and does not contain any incompressible surfaces.Orbifold Theorem. Let M be a small 3-manifold. Let φ be a non-trivial periodic orientation-preserving diffeomorphism of M. Then M admits a φ-invariant hyperbolic or Seifert fibered structure.
This theorem is a special case of Thurston's orbifold theorem, announced without proof in 1981; it forms part of his geometrization conjecture for 3-manifolds. In particular it implies that if X is a compact, connected, orientable, irreducible, atoroidal 3-orbifold with non-empty singular locus, then M has a geometric structure (in the sense of orbifolds). A complete proof of the theorem was published by Boileau, Leeb & Porti in 2005.
Orbifolds in string theory
In string theoryString theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the word "orbifold" has a slightly new meaning. For mathematicians, an orbifold is a generalization of the notion of manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
that allows the presence of the points whose neighborhood is diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to a quotient of Rn by a finite group, i.e. Rn/Γ. In physics, the notion of an orbifold usually describes an object that can be globally written as an orbit space M/G where M is a manifold (or a theory), and G is a group of its isometries (or symmetries) — not necessarily all of them. In string theory, these symmetries do not have to have a geometric interpretation.
A quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
defined on an orbifold becomes singular near the fixed points of G. However string theory requires us to add new parts of the closed string Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
— namely the twisted sectors where the fields defined on the closed strings are periodic up to an action from G. Orbifolding is therefore a general procedure of string theory to derive a new string theory from an old string theory in which the elements of G have been identified with the identity. Such a procedure reduces the number of states because the states must be invariant under G, but it also increases the number of states because of the extra twisted sectors. The result is usually a perfectly smooth, new string theory.
D-branes propagating on the orbifolds are described, at low energies, by gauge theories defined by the quiver diagram
Quiver diagram
In physics, a quiver diagram is a graph representing the matter content of a gauge theory that describes D-branes on orbifolds.Each node of the graph corresponds to a factor U of the gauge group, and each link represents a field in the bifundamental representation.The relevance of quiver diagrams...
s. Open strings attached to these D-branes have no twisted sector, and so the number of open string states is reduced by the orbifolding procedure.
More specifically, when the orbifold group G is a discrete subgroup of spacetime isometries, then if it has no fixed point, the result is usually a compact smooth space; the twisted sector consists of closed strings wound around the compact dimension, which are called
.When the orbifold group G is a discrete subgroup of spacetime isometries, and it has fixed points, then these usually have conical singularities, because Rn/Zk
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
has such a singularity at the fixed point of Zk
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. In string theory, gravitational singularities are usually a sign of extra degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
which are located at locus point in spacetime. In the case of the orbifold these degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
are the twisted states, which are strings "stuck" at the fixed points. When the fields related with these twisted states acquire a non-zero vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
, the singularity is deformed, i.e. the metric is changed and becomes regular at this point and around it. An example for a resulting geometry is the is Eguchi-Hanson spacetime.
From the point of view of D-branes in the vicinity of the fixed points, the effective theory of the open strings attached to these D-branes is a supersymmetric field theory, whose space of vacua has a singular point, where additional massless degrees of freedom exist. The fields related with the closed string twisted sector couple to the open strings in such a way as to add a Fayet-Iliopoulos term to the supersymmetric field theory Lagrangian, so that when such a field acquires a non-zero vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
, the Fayet-Iliopoulos term is non-zero, and thereby deforms the theory (i.e. changes it) so that the singularity no longer exists http://arxiv.org/abs/hep-th/9603167, http://www-spires.fnal.gov/spires/find/hep/www?j=NUPHA,B342,246.
Calabi–Yau manifolds
In superstring theorySuperstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
,
the construction of realistic phenomenological models requires dimensional reduction
Dimensional reduction
In physics, a theory in D spacetime dimensions can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions....
because the strings naturally propagate in a 10-dimensional space whilst the observed dimension of space-time of the universe is 4. Formal constraints on the theories nevertheless place restrictions on the compactified space
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
in which the extra "hidden" variables live: when looking for realistic 4-dimensional models with supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, the auxiliary compactified space must be a 6-dimensional Calabi-Yau manifold
Calabi-Yau manifold
A Calabi-Yau manifold is a special type of manifold that shows up in certain branches of mathematics such as algebraic geometry, as well as in theoretical physics...
.
There are a large number of possible Calabi-Yau manifolds (tens of thousands), whence the use of the term "swampland" in the current theoretical physics literature to describe the baffling choice. The general study of Calabi-Yau manifolds is mathematically complex and for a long time examples have been hard to construct explicitly. Orbifolds have therefore proved very useful since they automatically satisfy the constraints imposed by supersymmetry. They provide degenerate examples of Calabi-Yau manifolds due to their singular points, but this is completely acceptable from the point of view of theoretical physics. Such orbifolds are called "supersymmetric": they are technically easier to study than general Calabi-Yau manifolds. It is very often possible to associate a continuous family of non-singular Calabi-Yau manifolds to a singular supersymmetric orbifold. In 4 dimensions this can be illustrated using complex K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s:
- Every K3 surface admits 16 cycles of dimension 2 that are topologically equivalent to usual 2-spheres. Making the surface of these spheres tend to zero, the K3 surface develops 16 singularities. This limit represents a point on the boundary of the moduli spaceModuli spaceIn algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of K3 surfaces and corresponds to the orbifold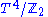
obtained by taking the quotient of the torus by the symmetry of inversion.
The study of Calabi-Yau manifolds in string theory and the duality between different models of string theory (type IIA and IIB) led to the idea of mirror symmetry in 1988. The role of orbifolds was first pointed out by Dixon, Harvey, Vafa and Witten around the same time.
Music theory
Beyond their manifold and various applications in mathematics and physics, orbifolds have been applied to music theoryMusic theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
in the work of Dmitri Tymoczko
Dmitri Tymoczko
Dmitri Tymoczko is a composer and music theorist. His music, which draws on rock, jazz, and romanticism, has been performed by ensembles such as the Ansermet Quartet, the Brentano Quartet, Janus, Newspeak, the San Francisco Contemporary Players, the Pacifica Quartet, and Ursula Opens...
and collaborators and . This is considered a sophisticated application of mathematics to music theory, with the resulting paper being the first music theory paper published by Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
.
Tymoczko models musical chords consisting of n notes, not necessarily distinct, as points in the orbifold
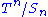– the space of n unordered points (not necessarily distinct) in the circle, realized as the quotient of the n-torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
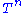(the space of n ordered points on the circle) by the symmetric group 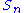(corresponding from moving from an ordered set to an unordered set).Musically, this is explained as follows:
- Musical tones depend on the frequency (pitch) of their fundamental, and thus are parametrized by the positive real numbers, R+.
- Musical tones that differ by an octave (a doubling of frequency) are considered the same tone – this corresponds to taking the logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
base 2 of frequencies (yielding the real numbers, as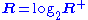
), then quotienting by the integers (corresponding to differing by some number of octaves), yielding a circle (as 
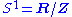). - Chords correspond to multiple tones without respect to order – thus t notes (with order) correspond to t ordered points on the torus, or equivalently a single point on the t-torus
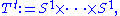and omitting order corresponds to taking the quotient by 
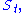yielding an orbifold.
For dyad
Dyad (music)
In music, a dyad is a set of two notes or pitches. Although most chords have three or more notes, in certain contexts a dyad may be considered to be a chord. The most common two-note chord is made from the interval of a perfect fifth, which may be suggestive of music of the Medieval or Renaissance...
s (two tones), this yields the closed Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
; for triad
Triad (music)
In music and music theory, a triad is a three-note chord that can be stacked in thirds. Its members, when actually stacked in thirds, from lowest pitched tone to highest, are called:* the Root...
s (three tones), this yields an orbifold that can be described as a triangular prism with the top and bottom triangular faces identified with a 120° twist (a ⅓ twist) – equivalently, as a solid torus in 3 dimensions with a cross-section an equilateral triangle and such a twist.
The resulting orbifold is naturally stratified by repeated tones (properly, by integer partitions of t) – the open set consists of distinct tones (the partition
), while there is a 1-dimensional singular set consisting of all tones being the same (the partition ), which topologically is a circle, and various intermediate partitions. There is also a notable circle which runs through the center of the open set consisting of equally spaced points. In the case of triads, the three side faces of the prism correspond to two tones being the same and the third different (the partition ), while the three edges of the prism correspond to the 1-dimensional singular set. The top and bottom faces are part of the open set, and only appear because the orbifold has been cut – if viewed as a triangular torus with a twist, these artifacts disappear.Tymoczko argues that chords close to the center (with tones equally or almost equally spaced) form the basis of much of traditional Western harmony, and that visualizing them in this way assists in analysis. There are 4 chords on the center (equally spaced under equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
– spacing of 4/4/4 between tones), corresponding to the augmented triad
Augmented triad
In music, an augmented triad is a triad, or chord, consisting of two major thirds . The term augmented triad arises from an augmented triad being a three note chord, or triad, whose top note is raised, or augmented...
s (thought of as musical sets
Set (music)
A set in music theory, as in mathematics and general parlance, is a collection of objects...
) C♯FA, DF♯A♯, D♯GB, and EG♯C (then they cycle: FAC♯ = C♯FA), with the 12 major chord
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
s and 12 minor chord
Minor chord
In music theory, a minor chord is a chord having a root, a minor third, and a perfect fifth.When a chord has these three notes alone, it is called a minor triad....
s being the points next to but not on the center – almost evenly spaced but not quite. Major chords correspond to 4/3/5 (or equivalently, 5/4/3) spacing, while minor chords correspond to 3/4/5 spacing. Key changes then correspond to movement between these points in the orbifold, with smoother changes effected by movement between nearby points.
See also
- Orbifold notation — a system popularized by the mathematician John Horton Conway for representing types of symmetry groups in two-dimensional spaces of constant curvature