
Differential form
Encyclopedia
In the mathematical
fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus
that is independent of coordinates. Differential forms provide a better definition for integrands in calculus. For instance, ƒ(x) dx is a 1-form which can be integrated
over an interval [a,b] in the domain of ƒ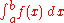
and similarly ƒ(x,y) dx + g(x,y) dy is a 1-form which has a line integral
over any oriented curve
γ in the domain of ƒ and g
Likewise, a 3-form ƒ(x, y, z) dx dy dz represents something that can be integrated over a region of space. The modern notion of differential forms was pioneered by Élie Cartan
, and has many applications, especially in geometry, topology and physics.
The algebra
of differential forms is organized in a way that naturally reflects the orientation
of the domain of integration. There is an operation d on differential forms known as the exterior derivative
that, when acting on a k-form produces a (k+1)-form. This operation extends the differential of a function
, and the divergence
and the curl of a vector field in an appropriate sense that makes the fundamental theorem of calculus
, the divergence theorem
, Green's theorem
, and Stokes' theorem
special cases of the same general result, known in this context also as Stokes' theorem. In a deeper way, this theorem relates the topology
of the domain of integration to the structure of the differential forms themselves; the precise connection is known as De Rham's theorem.
The general setting for the study of differential forms is on a differentiable manifold
. Differential 1-forms are naturally dual to vector field
s on a manifold, and the pairing between vector fields and 1-forms is extended to arbitrary differential forms by the interior product. The algebra of differential forms along with the exterior derivative defined on it is preserved by the pullback under smooth functions between two manifolds. This feature allows geometrically invariant information to be moved from one space to another via the pullback, provided the information is expressed in terms of differential forms. As a particular example, the change of variables formula for integration becomes a simple statement that an integral is preserved under pullback.
that is independent of coordinates.
Let U be an open set
in Rn. A differential 0-form ("zero form") is defined to be a smooth function
f on U. If v is any vector in Rn, then f has a directional derivative
∂v f, which is another function on U whose value at a point p ∈ U is the rate of change (at p) of f in the v direction:
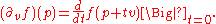
(This notion can be extended to the case that v is a vector field
on U by evaluating v at the point p in the definition.)
In particular, if v = ej is the jth coordinate vector
then ∂vf is the partial derivative
of f with respect to the jth coordinate function, i.e., ∂f / ∂xj, where x1, x2, ... xn are the coordinate functions on U. By their very definition, partial derivatives depend upon the choice of coordinates: if new coordinates y1, y2, ... yn are introduced, then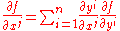
The first idea leading to differential forms is the observation that ∂v f (p) is a linear function
of v:
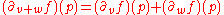
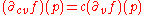
for any vectors v, w and any real number c. This linear map from Rn to R is denoted dfp and called the derivative
of f at p. Thus dfp(v) = ∂v f (p). The object df can be viewed as a function on U, whose value at p is not a real number, but the linear map dfp. This is just the usual Fréchet derivative
— an example of a differential 1-form.
Since any vector v is a linear combination
∑ vjej of its components, df is uniquely determined by dfp(ej) for each j and each p∈U, which are just the partial derivatives of f on U. Thus df provides a way of encoding the partial derivatives of f. It can be decoded by noticing that the coordinates x1, x2,... xn are themselves functions on U, and so define differential 1-forms dx1, dx2, ..., dxn. Since ∂xi / ∂xj = δij, the Kronecker delta function, it follows that
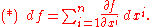
The meaning of this expression is given by evaluating both sides at an arbitrary point p: on the right hand side, the sum is defined "pointwise
", so that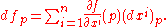
Applying both sides to ej, the result on each side is the jth partial derivative of f at p. Since p and j were arbitrary, this proves the formula (*).
More generally, for any smooth functions gi and hi on U, we define the differential 1-form α = ∑i gi dhi pointwise by

for each p ∈ U. Any differential 1-form arises this way, and by using (*) it follows that any differential 1-form α on U may be expressed in coordinates as
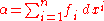
for some smooth functions fi on U.
The second idea leading to differential forms arises from the following question: given a differential 1-form α on U, when does there exist a function f on U such that α = df? The above expansion reduces this question to the search for a function f whose partial derivatives ∂f / ∂xi are equal to n given functions fi. For n>1, such a function does not always exist: any smooth function f satisfies

so it will be impossible to find such an f unless
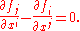
for all i and j.
The skew-symmetry of the left hand side in i and j suggests introducing an antisymmetric product on differential 1-forms, the wedge product, so that these equations can be combined into a single condition
on differential 1-forms, the wedge product, so that these equations can be combined into a single condition

where
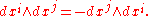
This is an example of a differential 2-form: the exterior derivative
dα of α= ∑j=1n fj dxj is given by
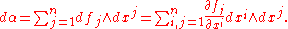
To summarize: dα = 0 is a necessary condition for the existence of a function f with α = df.
Differential 0-forms, 1-forms, and 2-forms are special cases of differential forms. For each k, there is a space of differential k-forms, which can be expressed in terms of the coordinates as
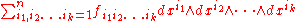
for a collection of functions fi1i2 ... ik. (Of course, as assumed below, one can restrict the sum to the case
Differential forms can be multiplied together using the wedge product, and for any differential k-form α, there is a differential (k + 1)-form dα called the exterior derivative of α.
Differential forms, the wedge product and the exterior derivative are independent of a choice of coordinates. Consequently they may be defined on any smooth manifold M. One way to do this is cover M with coordinate charts and define a differential k-form on M to be a family of differential k-forms on each chart which agree on the overlaps. However, there are more intrinsic definitions which make the independence of coordinates manifest.
of the kth exterior power
of the cotangent bundle
of M. At any point p∈M, a k-form β defines an alternating multilinear map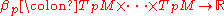
(with k factors of TpM in the product), where TpM is the tangent space
to M at p. Equivalently, β is a totally antisymmetric covariant tensor
field of rank k.
The set of all differential k-forms on a manifold M is a vector space
, often denoted Ωk(M).
For example, a differential 1-form α assigns to each point p∈M a linear functional
αp on TpM. In the presence of an inner product on TpM (induced by a Riemannian metric on M), αp may be represented
as the inner product with a tangent vector
Xp. Differential 1-forms are sometimes called covariant vector fields, covector fields, or "dual vector fields", particularly within physics.
of a single differential form, the interior product of a differential form and a vector field, and the Lie derivative
of a differential form with respect to a vector field.

for v, w ∈ TpM. (In an alternative convention, the right hand side is divided by two in this formula.)
The wedge product is bilinear: for instance, if α, β, and γ are any differential forms, then
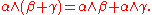
It is skew commutative (also known as graded commutative), meaning that it satisfies a variant of anticommutativity
that depends on the degrees of the forms: if α is a k-form and β is an l-form, then
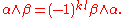
, or more generally a pseudo-Riemannian manifold
, vector fields and covector field can be identified (the metric is a fiber-wise isomorphism of the tangent space and the cotangent space), and additional operations can thus be defined, such as the Hodge star operator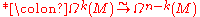 and codifferential
and codifferential 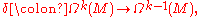 (degree
(degree 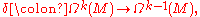 ) which is adjoint to the exterior differential d.
) which is adjoint to the exterior differential d.
Firstly, each tangent space (and thus vector fields) generate a Clifford algebra
. The product of two vectors in a Clifford algebra differs from the exterior product of k-vectors (dual to the exterior product of k-forms): In a Clifford algebra the square of a vector is computed by evaluating a quadratic form, whereas the exterior product of two k-vectors is always 0. Clifford algebras are a non-anti-commutative ("quantum") deformation of the exterior algebra. This structure is used in geometric algebra
.
Another alternative is to consider vector fields as derivations, and consider the (noncommutative) algebra of differential operator
s they generate, which is the Weyl algebra, and is a noncommutative ("quantum") deformation of the symmetric algebra in the vector fields.
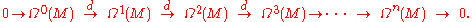
By the Poincaré lemma, this complex is locally exact
except at Ω0(M). Its cohomology
is the de Rham cohomology
of M.
Differential forms can be moved from one manifold to another using a smooth map. If f : M → N is smooth and ω is a smooth k-form on N, then there is a differential form f*ω on M, called the pullback of ω, which captures the behavior of ω as seen relative to f.
To define the pullback, recall that the differential of f is a map f* : TM → TN. Fix a differential k-form ω on N. For a point p of M and tangent vectors v1, ..., vk to M at p, the pullback of ω is defined by the formula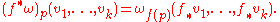
More abstractly, if ω is viewed as a section of the cotangent bundle T*N of N, then f*ω is the section of T*M defined as the composite map
Pullback respects all of the basic operations on forms:


The pullback of a form can also be written in coordinates. Assume that x1, ..., xm are coordinates on M, that y1, ..., yn are coordinates on N, and that these coordinate systems are related by the formulas yi = fi(x1, ..., xm) for all i. Then, locally on N, ω can be written as
where, for each choice of i1, ..., ik, is a real-valued function of y1, ..., yn. Using the linearity of pullback and its compatibility with wedge product, the pullback of ω has the formula
is a real-valued function of y1, ..., yn. Using the linearity of pullback and its compatibility with wedge product, the pullback of ω has the formula
Each exterior derivative dfi can be expanded in terms of dx1, ..., dxm. The resulting k-form can be written using Jacobian matrices: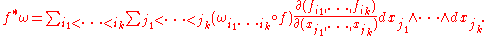
s. If k = 0, this is just evaluation of functions at points. Other values of k = 1, 2, 3, ... correspond to line integrals, surface integrals, volume integrals etc. Simply, a chain parametrizes a domain of integration as a collection of cells (images cubes or other domains D) that are patched together; to integrate, one pulls back the form on each cell of the chain to a form on the cube (or other domain) and integrates there, which is just integration of a function on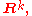 as the pulled back form is simply a multiple of the volume form
as the pulled back form is simply a multiple of the volume form
 For example, given a path
For example, given a path  integrating a form on the path is simply pulling back the form to a function on
integrating a form on the path is simply pulling back the form to a function on  (properly, to a form
(properly, to a form 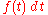 ) and integrating the function on the interval.
) and integrating the function on the interval.
Let
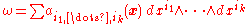
be a differential form and S a differentiable k-manifold
over which we wish to integrate, where S has the parameterization
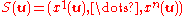
for u in the parameter domain D. Then defines the integral of the differential form over S as

where

is the determinant of the Jacobian. The Jacobian exists because S is differentiable.
More generally, a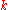 -form can be integrated over an
-form can be integrated over an  -dimensional submanifold, for
-dimensional submanifold, for  , to obtain a
, to obtain a  -form. This comes up, for example, in defining the pushforward of a differential form by a smooth map
-form. This comes up, for example, in defining the pushforward of a differential form by a smooth map 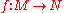 by attempting to integrate over the fibers of
by attempting to integrate over the fibers of  .
.
: If is an n−1-form with compact support on M and ∂M denotes the boundary
is an n−1-form with compact support on M and ∂M denotes the boundary
of M with its induced orientation
, then
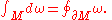
A key consequence of this is that "the integral of a closed form over homologous chains is equal": if is a closed k-form and M and N are k-chains that are homologous (such that M-N is the boundary of a (k+1)-chain W), then
is a closed k-form and M and N are k-chains that are homologous (such that M-N is the boundary of a (k+1)-chain W), then 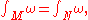 since the difference is the integral
since the difference is the integral 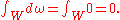
For example, if is the derivative of a potential function on the plane or
is the derivative of a potential function on the plane or 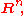 then the integral of
then the integral of  over a path from a to b does not depend on the choice of path (the integral is
over a path from a to b does not depend on the choice of path (the integral is 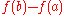 ), since different paths with given endpoints are homotopic, hence homologous (a weaker condition). This case is called the gradient theorem
), since different paths with given endpoints are homotopic, hence homologous (a weaker condition). This case is called the gradient theorem
, and generalizes the fundamental theorem of calculus
). This path independence is very useful in contour integration.
This theorem also underlies the duality between de Rham cohomology
and the homology
of chains.
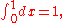 while
while 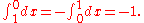 By contrast, the integral of the measure dx on the interval is unambiguously 1 (formally, the integral of the constant function 1 with respect to this measure is 1). Similarly, under a change of coordinates a differential n-form changes by the Jacobian determinant J, while a measure changes by the absolute value of the Jacobian determinant,
By contrast, the integral of the measure dx on the interval is unambiguously 1 (formally, the integral of the constant function 1 with respect to this measure is 1). Similarly, under a change of coordinates a differential n-form changes by the Jacobian determinant J, while a measure changes by the absolute value of the Jacobian determinant,  which further reflects the issue of orientation. For example, under the map
which further reflects the issue of orientation. For example, under the map  on the line, the differential form
on the line, the differential form 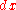 pulls back to
pulls back to 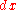 orientation has reversed; while the Lebesgue measure
orientation has reversed; while the Lebesgue measure
, also denoted pulls back to
pulls back to 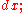 it does not change.
it does not change.
In the presence of the additional data of an orientation, it is possible to integrate n-forms (top-dimensional forms) over the entire manifold or over compact subsets; integration over the entire manifold corresponds to integrating the form over the fundamental class
of the manifold,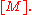 Formally, in the presence of an orientation, one may identify n-forms with densities on a manifold; densities in turn define a measure, and thus can be integrated .
Formally, in the presence of an orientation, one may identify n-forms with densities on a manifold; densities in turn define a measure, and thus can be integrated .
On an orientable but not oriented manifold, there are two choices of orientation; either choice allows one to integrate n-forms over compact subsets, with the two choices differing by a sign. On non-orientable manifold, n-forms and densities cannot be identified - notably, any top-dimensional form must vanish (there are no volume form
s on non-orientable manifolds), but there are non-vanishing densities - thus while one can integrate densities over compact subsets, one cannot integrate n-forms.
There is in general no meaningful way to integrate k-forms over subsets for because there is no consistent way to orient k-dimensional subsets; geometrically, a k-dimensional subset can be turned around in place, reversing any orientation but yielding the same subset. Compare the Gram determinant of a set of k vectors in an n-dimensional space, which, unlike the determinant of n vectors, is always positive, corresponding to a squared number.
because there is no consistent way to orient k-dimensional subsets; geometrically, a k-dimensional subset can be turned around in place, reversing any orientation but yielding the same subset. Compare the Gram determinant of a set of k vectors in an n-dimensional space, which, unlike the determinant of n vectors, is always positive, corresponding to a squared number.
On a Riemannian manifold, one may define a k-dimensional Hausdorff measure
for any k (integer or real), which may be integrated over k-dimensional subsets of the manifold. A function times this Hausdorff measure can then be integrated over k-dimensional subsets, providing a measure-theoretic analog to integration of k-forms. The n-dimensional Hausdorff measure yields a density, as above.
, the Faraday 2-form, or electromagnetic field strength, is
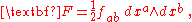
where the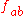 are formed from the electromagnetic fields
are formed from the electromagnetic fields 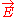 and
and 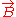 , e.g.
, e.g. 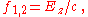
 , or equivalent definitions.
, or equivalent definitions.
This form is a special case of the curvature form
on the U(1) principal fiber bundle on which both electromagnetism and general gauge theories may be described. The connection form
for the principal bundle is the vector potential, typically denoted by A, when represented in some gauge. One then has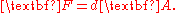
The current 3-form is

where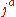 are the four components of the current-density. (Here it is a matter of convention, to write
are the four components of the current-density. (Here it is a matter of convention, to write  instead of
instead of 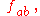 i.e. to use capital letters, and to write
i.e. to use capital letters, and to write 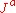 instead of
instead of 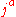 . However, it should be noted that the vector rsp. tensor components and the above-mentioned forms have different physical dimensions. Moreover, one should remember that by decision of an international commission of the IUPAP, the magnetic polarization vector is called
. However, it should be noted that the vector rsp. tensor components and the above-mentioned forms have different physical dimensions. Moreover, one should remember that by decision of an international commission of the IUPAP, the magnetic polarization vector is called  since several decades, and by some publishers
since several decades, and by some publishers 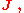 i.e. the same name is used for totally different quantities.)
i.e. the same name is used for totally different quantities.)
Using the above-mentioned definitions, Maxwell's equations
can be written very compactly in geometrized units as
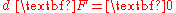

where denotes the Hodge star operator. Similar considerations describe the geometry of gauge theories in general.
denotes the Hodge star operator. Similar considerations describe the geometry of gauge theories in general.
The 2-form which is dual
which is dual
to the Faraday form, is also called Maxwell 2-form.
Electromagnetism is an example of a U(1) gauge theory
. Here U(1) is a Lie group
, the one-dimensional unitary group
, which is in particular abelian
. There are gauge theories, such as Yang-Mills theory, in which the group is not abelian. In that case, one gets relations which are similar to those described here. The analog of the field F in such theories is the curvature form of the connection, which is represented in a gauge by a Lie algebra
-valued one-form A. The field F is then defined by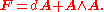
In the abelian case, such as electromagnetism, , but this does not hold in general. Likewise the field equations are modified by additional terms involving wedge products of A and F, owing to the structure equations of the gauge group.
, but this does not hold in general. Likewise the field equations are modified by additional terms involving wedge products of A and F, owing to the structure equations of the gauge group.
. A succinct proof may be found in Herbert Federer
's classic text Geometric Measure Theory. The Wirtinger inequality is also a key ingredient in Gromov's inequality for complex projective space in systolic geometry.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus
Multivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
that is independent of coordinates. Differential forms provide a better definition for integrands in calculus. For instance, ƒ(x) dx is a 1-form which can be integrated
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over an interval [a,b] in the domain of ƒ
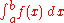
and similarly ƒ(x,y) dx + g(x,y) dy is a 1-form which has a line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
over any oriented curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
γ in the domain of ƒ and g

Likewise, a 3-form ƒ(x, y, z) dx dy dz represents something that can be integrated over a region of space. The modern notion of differential forms was pioneered by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, and has many applications, especially in geometry, topology and physics.
The algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of differential forms is organized in a way that naturally reflects the orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of the domain of integration. There is an operation d on differential forms known as the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
that, when acting on a k-form produces a (k+1)-form. This operation extends the differential of a function
Differential of a function
In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
, and the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and the curl of a vector field in an appropriate sense that makes the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
, the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
, and Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
special cases of the same general result, known in this context also as Stokes' theorem. In a deeper way, this theorem relates the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the domain of integration to the structure of the differential forms themselves; the precise connection is known as De Rham's theorem.
The general setting for the study of differential forms is on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
. Differential 1-forms are naturally dual to vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on a manifold, and the pairing between vector fields and 1-forms is extended to arbitrary differential forms by the interior product. The algebra of differential forms along with the exterior derivative defined on it is preserved by the pullback under smooth functions between two manifolds. This feature allows geometrically invariant information to be moved from one space to another via the pullback, provided the information is expressed in terms of differential forms. As a particular example, the change of variables formula for integration becomes a simple statement that an integral is preserved under pullback.
Concept
Differential forms provide an approach to multivariable calculusMultivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
that is independent of coordinates.
Let U be an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in Rn. A differential 0-form ("zero form") is defined to be a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
f on U. If v is any vector in Rn, then f has a directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
∂v f, which is another function on U whose value at a point p ∈ U is the rate of change (at p) of f in the v direction:
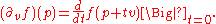
(This notion can be extended to the case that v is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on U by evaluating v at the point p in the definition.)
In particular, if v = ej is the jth coordinate vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
then ∂vf is the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of f with respect to the jth coordinate function, i.e., ∂f / ∂xj, where x1, x2, ... xn are the coordinate functions on U. By their very definition, partial derivatives depend upon the choice of coordinates: if new coordinates y1, y2, ... yn are introduced, then
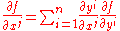
The first idea leading to differential forms is the observation that ∂v f (p) is a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
of v:
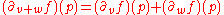
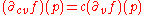
for any vectors v, w and any real number c. This linear map from Rn to R is denoted dfp and called the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of f at p. Thus dfp(v) = ∂v f (p). The object df can be viewed as a function on U, whose value at p is not a real number, but the linear map dfp. This is just the usual Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
— an example of a differential 1-form.
Since any vector v is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
∑ vjej of its components, df is uniquely determined by dfp(ej) for each j and each p∈U, which are just the partial derivatives of f on U. Thus df provides a way of encoding the partial derivatives of f. It can be decoded by noticing that the coordinates x1, x2,... xn are themselves functions on U, and so define differential 1-forms dx1, dx2, ..., dxn. Since ∂xi / ∂xj = δij, the Kronecker delta function, it follows that
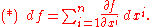
The meaning of this expression is given by evaluating both sides at an arbitrary point p: on the right hand side, the sum is defined "pointwise
Pointwise
In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
", so that
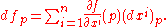
Applying both sides to ej, the result on each side is the jth partial derivative of f at p. Since p and j were arbitrary, this proves the formula (*).
More generally, for any smooth functions gi and hi on U, we define the differential 1-form α = ∑i gi dhi pointwise by

for each p ∈ U. Any differential 1-form arises this way, and by using (*) it follows that any differential 1-form α on U may be expressed in coordinates as
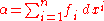
for some smooth functions fi on U.
The second idea leading to differential forms arises from the following question: given a differential 1-form α on U, when does there exist a function f on U such that α = df? The above expansion reduces this question to the search for a function f whose partial derivatives ∂f / ∂xi are equal to n given functions fi. For n>1, such a function does not always exist: any smooth function f satisfies

so it will be impossible to find such an f unless
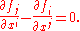
for all i and j.
The skew-symmetry of the left hand side in i and j suggests introducing an antisymmetric product
 on differential 1-forms, the wedge product, so that these equations can be combined into a single condition
on differential 1-forms, the wedge product, so that these equations can be combined into a single condition
where
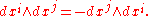
This is an example of a differential 2-form: the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
dα of α= ∑j=1n fj dxj is given by
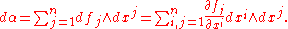
To summarize: dα = 0 is a necessary condition for the existence of a function f with α = df.
Differential 0-forms, 1-forms, and 2-forms are special cases of differential forms. For each k, there is a space of differential k-forms, which can be expressed in terms of the coordinates as
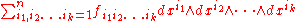
for a collection of functions fi1i2 ... ik. (Of course, as assumed below, one can restrict the sum to the case

Differential forms can be multiplied together using the wedge product, and for any differential k-form α, there is a differential (k + 1)-form dα called the exterior derivative of α.
Differential forms, the wedge product and the exterior derivative are independent of a choice of coordinates. Consequently they may be defined on any smooth manifold M. One way to do this is cover M with coordinate charts and define a differential k-form on M to be a family of differential k-forms on each chart which agree on the overlaps. However, there are more intrinsic definitions which make the independence of coordinates manifest.
Intrinsic definitions
Let M be a smooth manifold. A differential form of degree k is a smooth sectionSection (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the kth exterior power
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of M. At any point p∈M, a k-form β defines an alternating multilinear map
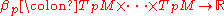
(with k factors of TpM in the product), where TpM is the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to M at p. Equivalently, β is a totally antisymmetric covariant tensor
Tensor (intrinsic definition)
In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
field of rank k.
The set of all differential k-forms on a manifold M is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, often denoted Ωk(M).
For example, a differential 1-form α assigns to each point p∈M a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
αp on TpM. In the presence of an inner product on TpM (induced by a Riemannian metric on M), αp may be represented
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
as the inner product with a tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
Xp. Differential 1-forms are sometimes called covariant vector fields, covector fields, or "dual vector fields", particularly within physics.
Operations
There are several operations on differential forms: the wedge product of two differential forms, the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of a single differential form, the interior product of a differential form and a vector field, and the Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of a differential form with respect to a vector field.
Wedge product
The wedge product of a k-form α and an l-form β is a (k + l)-form denoted αΛβ. For example, if k = l = 1, then αΛβ is the 2-form whose value at a point p is the alternating bilinear form defined by
for v, w ∈ TpM. (In an alternative convention, the right hand side is divided by two in this formula.)
The wedge product is bilinear: for instance, if α, β, and γ are any differential forms, then
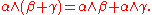
It is skew commutative (also known as graded commutative), meaning that it satisfies a variant of anticommutativity
Anticommutativity
In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
that depends on the degrees of the forms: if α is a k-form and β is an l-form, then
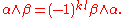
Riemannian manifold
On a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, or more generally a pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, vector fields and covector field can be identified (the metric is a fiber-wise isomorphism of the tangent space and the cotangent space), and additional operations can thus be defined, such as the Hodge star operator
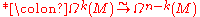 and codifferential
and codifferential 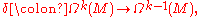 (degree
(degree 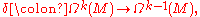 ) which is adjoint to the exterior differential d.
) which is adjoint to the exterior differential d.Vector field structures
On a pseudo-Riemannian manifold, 1-forms can be identified with vector fields; vector fields have additional distinct algebraic structures, which are listed here for context and to avoid confusion.Firstly, each tangent space (and thus vector fields) generate a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. The product of two vectors in a Clifford algebra differs from the exterior product of k-vectors (dual to the exterior product of k-forms): In a Clifford algebra the square of a vector is computed by evaluating a quadratic form, whereas the exterior product of two k-vectors is always 0. Clifford algebras are a non-anti-commutative ("quantum") deformation of the exterior algebra. This structure is used in geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
.
Another alternative is to consider vector fields as derivations, and consider the (noncommutative) algebra of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s they generate, which is the Weyl algebra, and is a noncommutative ("quantum") deformation of the symmetric algebra in the vector fields.
Exterior differential complex
One important property of the exterior derivative is that d2 = 0. This means that the exterior derivative defines a cochain complex: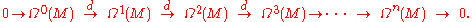
By the Poincaré lemma, this complex is locally exact
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
except at Ω0(M). Its cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
is the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
of M.
Pullback
One of the main reasons the cotangent bundle rather than the tangent bundle is used in the construction of the exterior complex is that differential forms are capable of being pulled back by smooth maps, while vector fields cannot be pushed forward by smooth maps unless the map is, say, a diffeomorphism. The existence of pullback homomorphisms in de Rham cohomology depends on the pullback of differential forms.Differential forms can be moved from one manifold to another using a smooth map. If f : M → N is smooth and ω is a smooth k-form on N, then there is a differential form f*ω on M, called the pullback of ω, which captures the behavior of ω as seen relative to f.
To define the pullback, recall that the differential of f is a map f* : TM → TN. Fix a differential k-form ω on N. For a point p of M and tangent vectors v1, ..., vk to M at p, the pullback of ω is defined by the formula
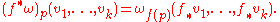
More abstractly, if ω is viewed as a section of the cotangent bundle T*N of N, then f*ω is the section of T*M defined as the composite map

Pullback respects all of the basic operations on forms:



The pullback of a form can also be written in coordinates. Assume that x1, ..., xm are coordinates on M, that y1, ..., yn are coordinates on N, and that these coordinate systems are related by the formulas yi = fi(x1, ..., xm) for all i. Then, locally on N, ω can be written as

where, for each choice of i1, ..., ik,
 is a real-valued function of y1, ..., yn. Using the linearity of pullback and its compatibility with wedge product, the pullback of ω has the formula
is a real-valued function of y1, ..., yn. Using the linearity of pullback and its compatibility with wedge product, the pullback of ω has the formula
Each exterior derivative dfi can be expanded in terms of dx1, ..., dxm. The resulting k-form can be written using Jacobian matrices:
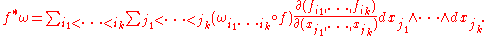
Integration
Differential forms of degree k are integrated over k dimensional chainChain (algebraic topology)
In algebraic topology, a simplicial k-chainis a formal linear combination of k-simplices.-Integration on chains:Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients typically integers.The set of all k-chains forms a group...
s. If k = 0, this is just evaluation of functions at points. Other values of k = 1, 2, 3, ... correspond to line integrals, surface integrals, volume integrals etc. Simply, a chain parametrizes a domain of integration as a collection of cells (images cubes or other domains D) that are patched together; to integrate, one pulls back the form on each cell of the chain to a form on the cube (or other domain) and integrates there, which is just integration of a function on
 as the pulled back form is simply a multiple of the volume form
as the pulled back form is simply a multiple of the volume formVolume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
 For example, given a path
For example, given a path  integrating a form on the path is simply pulling back the form to a function on
integrating a form on the path is simply pulling back the form to a function on 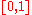 (properly, to a form
(properly, to a form 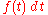 ) and integrating the function on the interval.
) and integrating the function on the interval.Let
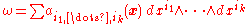
be a differential form and S a differentiable k-manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
over which we wish to integrate, where S has the parameterization
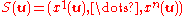
for u in the parameter domain D. Then defines the integral of the differential form over S as

where

is the determinant of the Jacobian. The Jacobian exists because S is differentiable.
More generally, a
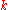 -form can be integrated over an
-form can be integrated over an  -dimensional submanifold, for
-dimensional submanifold, for  , to obtain a
, to obtain a  -form. This comes up, for example, in defining the pushforward of a differential form by a smooth map
-form. This comes up, for example, in defining the pushforward of a differential form by a smooth map 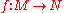 by attempting to integrate over the fibers of
by attempting to integrate over the fibers of  .
.Stokes' theorem
The fundamental relationship between the exterior derivative and integration is given by the general Stokes theoremStokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
: If
 is an n−1-form with compact support on M and ∂M denotes the boundary
is an n−1-form with compact support on M and ∂M denotes the boundaryManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of M with its induced orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, then
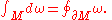
A key consequence of this is that "the integral of a closed form over homologous chains is equal": if
 is a closed k-form and M and N are k-chains that are homologous (such that M-N is the boundary of a (k+1)-chain W), then
is a closed k-form and M and N are k-chains that are homologous (such that M-N is the boundary of a (k+1)-chain W), then 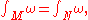 since the difference is the integral
since the difference is the integral 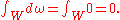
For example, if
 is the derivative of a potential function on the plane or
is the derivative of a potential function on the plane or 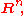 then the integral of
then the integral of  over a path from a to b does not depend on the choice of path (the integral is
over a path from a to b does not depend on the choice of path (the integral is 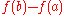 ), since different paths with given endpoints are homotopic, hence homologous (a weaker condition). This case is called the gradient theorem
), since different paths with given endpoints are homotopic, hence homologous (a weaker condition). This case is called the gradient theoremGradient theorem
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L...
, and generalizes the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
). This path independence is very useful in contour integration.
This theorem also underlies the duality between de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
and the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of chains.
Relation with measures
On a general differentiable manifold (without additional structure), differential forms cannot be integrated over subsets of the manifold; this distinction is key to the distinction between differential forms, which are integrated over chains, and measures, which are integrated over subsets. The simplest example is attempting to integrate the 1-form dx over the interval [0,1]. Assuming the usual distance (and thus measure) on the real line, this integral is either 1 or −1, depending on orientation: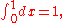 while
while 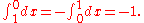 By contrast, the integral of the measure dx on the interval is unambiguously 1 (formally, the integral of the constant function 1 with respect to this measure is 1). Similarly, under a change of coordinates a differential n-form changes by the Jacobian determinant J, while a measure changes by the absolute value of the Jacobian determinant,
By contrast, the integral of the measure dx on the interval is unambiguously 1 (formally, the integral of the constant function 1 with respect to this measure is 1). Similarly, under a change of coordinates a differential n-form changes by the Jacobian determinant J, while a measure changes by the absolute value of the Jacobian determinant,  which further reflects the issue of orientation. For example, under the map
which further reflects the issue of orientation. For example, under the map  on the line, the differential form
on the line, the differential form 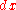 pulls back to
pulls back to 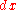 orientation has reversed; while the Lebesgue measure
orientation has reversed; while the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, also denoted
 pulls back to
pulls back to 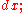 it does not change.
it does not change.In the presence of the additional data of an orientation, it is possible to integrate n-forms (top-dimensional forms) over the entire manifold or over compact subsets; integration over the entire manifold corresponds to integrating the form over the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
of the manifold,
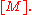 Formally, in the presence of an orientation, one may identify n-forms with densities on a manifold; densities in turn define a measure, and thus can be integrated .
Formally, in the presence of an orientation, one may identify n-forms with densities on a manifold; densities in turn define a measure, and thus can be integrated .On an orientable but not oriented manifold, there are two choices of orientation; either choice allows one to integrate n-forms over compact subsets, with the two choices differing by a sign. On non-orientable manifold, n-forms and densities cannot be identified - notably, any top-dimensional form must vanish (there are no volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
s on non-orientable manifolds), but there are non-vanishing densities - thus while one can integrate densities over compact subsets, one cannot integrate n-forms.
There is in general no meaningful way to integrate k-forms over subsets for
 because there is no consistent way to orient k-dimensional subsets; geometrically, a k-dimensional subset can be turned around in place, reversing any orientation but yielding the same subset. Compare the Gram determinant of a set of k vectors in an n-dimensional space, which, unlike the determinant of n vectors, is always positive, corresponding to a squared number.
because there is no consistent way to orient k-dimensional subsets; geometrically, a k-dimensional subset can be turned around in place, reversing any orientation but yielding the same subset. Compare the Gram determinant of a set of k vectors in an n-dimensional space, which, unlike the determinant of n vectors, is always positive, corresponding to a squared number.On a Riemannian manifold, one may define a k-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
for any k (integer or real), which may be integrated over k-dimensional subsets of the manifold. A function times this Hausdorff measure can then be integrated over k-dimensional subsets, providing a measure-theoretic analog to integration of k-forms. The n-dimensional Hausdorff measure yields a density, as above.
Applications in physics
Differential forms arise in some important physical contexts. For example, in Maxwell's theory of electromagnetismElectromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, the Faraday 2-form, or electromagnetic field strength, is
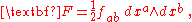
where the
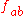 are formed from the electromagnetic fields
are formed from the electromagnetic fields 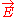 and
and 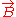 , e.g.
, e.g. 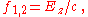
 , or equivalent definitions.
, or equivalent definitions.This form is a special case of the curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
on the U(1) principal fiber bundle on which both electromagnetism and general gauge theories may be described. The connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
for the principal bundle is the vector potential, typically denoted by A, when represented in some gauge. One then has
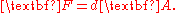
The current 3-form is

where
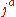 are the four components of the current-density. (Here it is a matter of convention, to write
are the four components of the current-density. (Here it is a matter of convention, to write  instead of
instead of 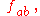 i.e. to use capital letters, and to write
i.e. to use capital letters, and to write 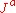 instead of
instead of 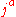 . However, it should be noted that the vector rsp. tensor components and the above-mentioned forms have different physical dimensions. Moreover, one should remember that by decision of an international commission of the IUPAP, the magnetic polarization vector is called
. However, it should be noted that the vector rsp. tensor components and the above-mentioned forms have different physical dimensions. Moreover, one should remember that by decision of an international commission of the IUPAP, the magnetic polarization vector is called  since several decades, and by some publishers
since several decades, and by some publishers 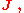 i.e. the same name is used for totally different quantities.)
i.e. the same name is used for totally different quantities.)Using the above-mentioned definitions, Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
can be written very compactly in geometrized units as
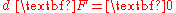

where
 denotes the Hodge star operator. Similar considerations describe the geometry of gauge theories in general.
denotes the Hodge star operator. Similar considerations describe the geometry of gauge theories in general.The 2-form
 which is dual
which is dualDual
Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
to the Faraday form, is also called Maxwell 2-form.
Electromagnetism is an example of a U(1) gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
. Here U(1) is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, the one-dimensional unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
, which is in particular abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. There are gauge theories, such as Yang-Mills theory, in which the group is not abelian. In that case, one gets relations which are similar to those described here. The analog of the field F in such theories is the curvature form of the connection, which is represented in a gauge by a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
-valued one-form A. The field F is then defined by
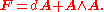
In the abelian case, such as electromagnetism,
 , but this does not hold in general. Likewise the field equations are modified by additional terms involving wedge products of A and F, owing to the structure equations of the gauge group.
, but this does not hold in general. Likewise the field equations are modified by additional terms involving wedge products of A and F, owing to the structure equations of the gauge group.Applications in geometric measure theory
Numerous minimality results for complex analytic manifolds are based on the Wirtinger inequality for 2-formsWirtinger inequality (2-forms)
In mathematics, the Wirtinger inequality for 2-forms, named after Wilhelm Wirtinger, states that the exterior \scriptstyle\nuth power of the standard symplectic form ω, when evaluated on a simple -vector ζ of unit volume, is bounded above by \scriptstyle\nu!...
. A succinct proof may be found in Herbert Federer
Herbert Federer
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
's classic text Geometric Measure Theory. The Wirtinger inequality is also a key ingredient in Gromov's inequality for complex projective space in systolic geometry.
See also
- Closed and exact differential formsClosed and exact differential formsIn mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
- complex differential formComplex differential formIn mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
- vector-valued differential form

