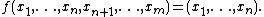Submersion (mathematics)
Encyclopedia
In mathematics
, a submersion is a differentiable map between differentiable manifold
s whose differential is everywhere surjective. This is a basic concept in differential topology
. The notion of a submersion is dual to the notion of an immersion.
s,
Let M and N be differentiable manifold
s and ƒ : M → N be a differentiable map between them. The map ƒ is a submersion at a point p ∈ M if its differential
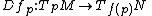
is a surjective linear map. In this case p is called a regular point of the map ƒ, otherwise, p is a singular point. A point q ∈ N is a regular value of ƒ if all points p in the pre-image ƒ−1(q) are regular points. A differentiable map ƒ that is a submersion at each point is called a submersion. Equivalently, ƒ is a submersion if its differential Dfp has constant rank equal to the dimension of N.
If the dimension of M is greater than or equal to the dimension of N then the points at which Dfp fails to be a surjection are the critical points
of ƒ, because the rank
of the Jacobian matrix of ƒ at p is not maximal. Thus in this case, the notions of a singular point and a critical point coincide. In the opposite case, when the dimension of M is less than the dimension of N, all points are singular. Critical points are the basic objects of study in Morse theory
(N = R, ƒ is a real-valued function) and the singularity theory
of differentiable maps (in general).
It follows that the full pre-image ƒ−1(q) in M of a regular value q ∈ N under a differentiable map ƒ: M → N is either empty or is a differentiable manifold of dimension dim M − dim N, possibly disconnected. This is the content of the regular value theorem (also known as the submersion theorem). In particular, the conclusion holds for all q ∈ N if the map ƒ is a submersion.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a submersion is a differentiable map between differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s whose differential is everywhere surjective. This is a basic concept in differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
. The notion of a submersion is dual to the notion of an immersion.
Definition
The general definition of a submersion applies to arbitrary differentiable manifolds, but in many interesting examples these manifolds are open subsets of Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s,
Let M and N be differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s and ƒ : M → N be a differentiable map between them. The map ƒ is a submersion at a point p ∈ M if its differential
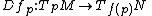
is a surjective linear map. In this case p is called a regular point of the map ƒ, otherwise, p is a singular point. A point q ∈ N is a regular value of ƒ if all points p in the pre-image ƒ−1(q) are regular points. A differentiable map ƒ that is a submersion at each point is called a submersion. Equivalently, ƒ is a submersion if its differential Dfp has constant rank equal to the dimension of N.
If the dimension of M is greater than or equal to the dimension of N then the points at which Dfp fails to be a surjection are the critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of ƒ, because the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of the Jacobian matrix of ƒ at p is not maximal. Thus in this case, the notions of a singular point and a critical point coincide. In the opposite case, when the dimension of M is less than the dimension of N, all points are singular. Critical points are the basic objects of study in Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
(N = R, ƒ is a real-valued function) and the singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
of differentiable maps (in general).
Examples
- Any projection
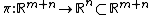
- Local diffeomorphismLocal diffeomorphismIn mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
s
- Riemannian submersionRiemannian submersionIn differential geometry, a branch of mathematics, a Riemannian submersion is a submersion from one Riemannian manifold to another that respects the metrics, meaning that it is an orthogonal projection on tangent spaces....
s
- The projection in a smooth vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
or a more general smooth fibrationFibrationIn topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
. The surjectivity of the differential is a necessary condition for the existence of a local trivialization.
Local normal form
If ƒ: M → N is a submersion at p and ƒ(p) = q ∈ N then there exist an open neighborhood U of p in M, an open neighborhood V of q in N, and local coordinates (x1,…,xm) at p and (x1,…,xn) at q such that ƒ(U) = V and the map ƒ in these local coordinates is the standard projectionIt follows that the full pre-image ƒ−1(q) in M of a regular value q ∈ N under a differentiable map ƒ: M → N is either empty or is a differentiable manifold of dimension dim M − dim N, possibly disconnected. This is the content of the regular value theorem (also known as the submersion theorem). In particular, the conclusion holds for all q ∈ N if the map ƒ is a submersion.