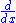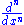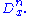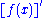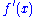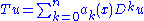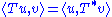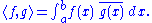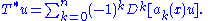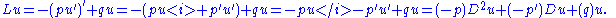Differential operator
Encyclopedia
In mathematics
, a differential operator is an operator defined as a function of the differentiation
operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another (in the style of a higher-order function
in computer science
).
This article considers only linear operators, even though the Schwarzian derivative
is a prominent example of a non-linear operator.
First derivatives are signified as above, but when taking higher, nth derivatives, the following alterations are useful:
For a function f of an argument x, the derivative operator is sometimes given as either of the following:
The D notation's use and creation is credited to Oliver Heaviside
, who considered differential operators of the form
in his study of differential equation
s.
One of the most frequently seen differential operators is the Laplacian operator
, defined by
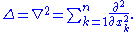
Another differential operator is the Θ operator, or theta operator, defined by
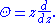
This is sometimes also called the homogeneity operator, because its eigenfunction
s are the monomials
in z:
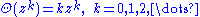
In n variables the homogeneity operator is given by
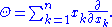
As in one variable, the eigenspaces of Θ are the spaces of homogeneous polynomial
s.
the adjoint of this operator
is defined as the operator such that
such that
where the notation is used for the scalar product or inner product. This definition therefore depends on the definition of the scalar product.
is used for the scalar product or inner product. This definition therefore depends on the definition of the scalar product.
If one moreover adds the condition that f or g vanishes for and
and  , one can also define the adjoint of T by
, one can also define the adjoint of T by
This formula does not explicitly depend on the definition of the scalar product. It is therefore sometimes chosen as a definition of the adjoint operator. When is defined according to this formula, it is called the formal adjoint of T.
is defined according to this formula, it is called the formal adjoint of T.
A (formally) self-adjoint
operator is an operator equal to its own (formal) adjoint.
by duality in the analogous manner:

for all smooth L2 functions f, g. Since smooth functions are dense in L2, this defines the adjoint on a dense subset of L2: P* is a densely-defined operator
.
This property can be proven using the formal adjoint definition above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a differential operator is an operator defined as a function of the differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another (in the style of a higher-order function
Higher-order function
In mathematics and computer science, higher-order functions, functional forms, or functionals are functions which do at least one of the following:*take one or more functions as an input*output a function...
in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
).
This article considers only linear operators, even though the Schwarzian derivative
Schwarzian derivative
In mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and...
is a prominent example of a non-linear operator.
Notations
The most commonly used differential operator is the action of taking the derivative itself. Common notations for this operator include:-
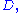 where the variable with respect to which one is differentiating is clear, and
where the variable with respect to which one is differentiating is clear, and
-
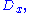 where the variable is declared explicitly.
where the variable is declared explicitly.
-
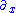 , is an alternative notation.
, is an alternative notation.
First derivatives are signified as above, but when taking higher, nth derivatives, the following alterations are useful:
For a function f of an argument x, the derivative operator is sometimes given as either of the following:
The D notation's use and creation is credited to Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
, who considered differential operators of the form
in his study of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s.
One of the most frequently seen differential operators is the Laplacian operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, defined by
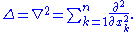
Another differential operator is the Θ operator, or theta operator, defined by
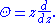
This is sometimes also called the homogeneity operator, because its eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s are the monomials
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
in z:
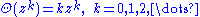
In n variables the homogeneity operator is given by
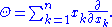
As in one variable, the eigenspaces of Θ are the spaces of homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s.
Adjoint of an operator
Given a linear differential operator Tthe adjoint of this operator
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
is defined as the operator
 such that
such that
where the notation
 is used for the scalar product or inner product. This definition therefore depends on the definition of the scalar product.
is used for the scalar product or inner product. This definition therefore depends on the definition of the scalar product.Formal adjoint in one variable
In the functional space of square integrable functions, the scalar product is defined byIf one moreover adds the condition that f or g vanishes for
 and
and  , one can also define the adjoint of T by
, one can also define the adjoint of T byThis formula does not explicitly depend on the definition of the scalar product. It is therefore sometimes chosen as a definition of the adjoint operator. When
 is defined according to this formula, it is called the formal adjoint of T.
is defined according to this formula, it is called the formal adjoint of T.A (formally) self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
operator is an operator equal to its own (formal) adjoint.
Several variables
If Ω is a domain in Rn, and P a differential operator on Ω, then the adjoint of P is defined in L2(Ω)Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
by duality in the analogous manner:

for all smooth L2 functions f, g. Since smooth functions are dense in L2, this defines the adjoint on a dense subset of L2: P* is a densely-defined operator
Densely-defined operator
In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere"...
.
Example
The Sturm–Liouville operator is a well-known example of formal self-adjoint operator. This second-order linear differential operator L can be written in the formThis property can be proven using the formal adjoint definition above.
-

This operator is central to Sturm–Liouville theory where the eigenfunctions (analogues to eigenvectors) of this operator are considered.
Properties of differential operators
Differentiation is linearLinearity of differentiationIn mathematics, the linearity of differentiation is a most fundamental property of the derivative, in differential calculus. It follows from the sum rule in differentiation and the constant factor rule in differentiation...
, i.e.,
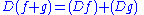
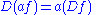
where f and g are functions, and a is a constant.
Any polynomial in D with function coefficients is also a differential operator. We may also compose differential operators by the rule
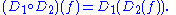
Some care is then required: firstly any function coefficients in the operator D2 must be differentiable as many times as the application of D1 requires. To get a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of such operators we must assume derivatives of all orders of the coefficients used. Secondly, this ring will not be commutative: an operator gD isn't the same in general as Dg. In fact we have for example the relation basic in quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
:
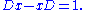
The subring of operators that are polynomials in D with constant coefficientsConstant coefficientsIn mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
is, by contrast, commutative. It can be characterised another way: it consists of the translation-invariant operators.
The differential operators also obey the shift theoremShift theoremIn mathematics, the shift theorem is a theorem about polynomial differential operators and exponential functions...
.
Several variables
The same constructions can be carried out with partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s, differentiation with respect to different variables giving rise to operators that commute (see symmetry of second derivativesSymmetry of second derivativesIn mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a functionfof n variables...
).
Coordinate-independent description
In differential geometry and algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
it is often convenient to have a coordinate-independent description of differential operators between two vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s. Let E and F be two vector bundles over a differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M. An R-linear mapping of sectionsVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
is said to be a kth-order linear differential operator if it factors through the jet bundleJet bundleIn differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
Jk(E).
In other words, there exists a linear mapping of vector bundles
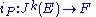
such that

where is the prolongation that associates to any section of E its k-jetJet (mathematics)In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
.
This just means that for a given sectionsVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s of E, the value of P(s) at a point x ∈ M is fully determined by the kth-order infinitesimal behavior of s in x. In particular this implies that P(s)(x) is determined by the germSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of s in x, which is expressed by saying that differential operators are local. A foundational result is the Peetre theoremPeetre theoremIn mathematics, the Peetre theorem, named after Jaak Peetre, is a result of functional analysis that gives a characterisation of differential operators in terms of their effect on generalized function spaces, and without mentioning differentiation in explicit terms...
showing that the converse is also true: any (linear) local operator is differential.
Relation to commutative algebra
An equivalent, but purely algebraic description of linear differential operators is as follows: an R-linear map P is a kth-order linear differential operator, if for any k + 1 smooth functions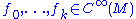 we have
we have

Here the bracket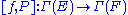 is defined as the commutator
is defined as the commutator
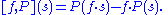
This characterization of linear differential operators shows that they are particular mappings between modulesModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a commutative algebraAlgebra (ring theory)In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
, allowing the concept to be seen as a part of commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
.
Examples
- In applications to the physical sciences, operators such as the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
play a major role in setting up and solving partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
- In differential topologyDifferential topologyIn mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
and Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
operators have intrinsic meaning.
- In abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the concept of a derivationDerivation (abstract algebra)In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
allows for generalizations of differential operators which do not require the use of calculus. Frequently such generalizations are employed in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
. See also jet (mathematics)Jet (mathematics)In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
.
See also
- Difference operator
- Delta operator
- Elliptic operatorElliptic operatorIn the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
- Fractional calculusFractional calculusFractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
- Invariant differential operator
- Differential calculus over commutative algebrasDifferential calculus over commutative algebrasIn mathematics the differential calculus over commutative algebras is a part of commutative algebra based on the observation that most concepts known from classical differential calculus can be formulated in purely algebraic terms...
- Lagrangian systemLagrangian systemIn mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
- In applications to the physical sciences, operators such as the Laplace operator