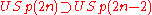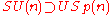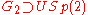Symplectic group
Encyclopedia
In mathematics
, the name symplectic group can refer to two different, but closely related, types of mathematical groups
, denoted Sp(2n, F) and Sp(n). The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually differing by factors of 2. The notation used here is consistent with the size of the matrices used to represent the groups. In Cartan
's classification of the simple Lie algebras, the Lie algebra of the complex group Sp(2n, C) is denoted Cn, and Sp(n) is the compact real form of Sp(2n, C).
The name "symplectic group" is due to Hermann Weyl
(details) as a replacement for the previous confusing names of (line) complex group and Abelian group, and is the Greek analog of "complex".
F, denoted Sp(2n, F), is the group of 2n by 2n symplectic matrices with entries in F, and with the group operation that of matrix multiplication
. Since all symplectic matrices have determinant
1, the symplectic group is a subgroup
of the special linear group
SL(2n, F).
More abstractly, the symplectic group can be defined as the set of linear transformations of a 2n-dimensional vector space
over F that preserve a nondegenerate, skew-symmetric, bilinear form. Such a vector space is called a symplectic vector space
. The symplectic group of an abstract symplectic vector space V is also denoted Sp(V).
When n = 1, the symplectic condition on a matrix is satisfied if and only if
the determinant is one, so that Sp(2, F) = SL(2, F). For n > 1, there are additional conditions, i.e. Sp(2n, F) is then a proper subgroup of SL(2n, F).
Typically, the field F is the field of real number
s, R, or complex number
s, C. In this case Sp(2n, F) is a real/complex Lie group
of real/complex dimension n(2n + 1). These groups are connected
but noncompact
. Sp(2n, C) is simply connected while Sp(2n, R) has a fundamental group
isomorphic to Z.
The Lie algebra
of Sp(2n, F) is given by the set of 2n×2n matrices A (with entries in F) that satisfy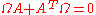
where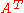
is the transpose
of A and Ω is the skew-symmetric matrix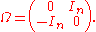
ic matrices) which preserves the standard hermitian form on Hn: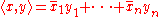
That is, Sp(n) is just the quaternionic unitary group
, U(n, H). Indeed, it is sometimes called the hyperunitary group. Also Sp(1) is the group of quaternions of unit 1, equivalent to SU(2) and topologically a 3-sphere
S3.
Note that Sp(n) is not a symplectic group in the sense of the previous section—it does not preserve a non-degenerate skew-symmetric (H-bilinear) form on Hn (in fact, the only skew-symmetric form is the zero form).
Rather, it is isomorphic to a subgroup of Sp(2n,C), and so does preserve a complex symplectic form in a vector space of dimension twice as high.
As explained below, the Lie algebra of Sp(n) is a real form of the complex symplectic Lie algebra sp(2n, C).
Sp(n) is a real Lie group with (real) dimension n(2n + 1). It is compact
, connected
, and simply connected. It can be defined by the intersection Sp(n)=U(2n) ∩ Sp(2n, C), where U(2n) stands for the unitary group.
The Lie algebra of Sp(n) is given by the quaternionic skew-Hermitian
matrices, the set of n by n quaternionic matrices that satisfy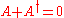
where
is the conjugate transpose
of A (here one takes the quaternionic conjugate). The Lie bracket is given by the commutator.
s. It turns out that the first of these Lie algebras is a complexification
of the Lie algebras of either of the latter two groups.
Stated slightly differently, the complex Lie algebra sp(2n, C) of the complex Lie group Sp(2n, C) has several different real forms:
The symplectic groups are also subgroups of various Lie groups:
There are also the isomorphism
s of the Lie algebras usp(4) = o(5) and usp(2) = o(3) = su(2).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the name symplectic group can refer to two different, but closely related, types of mathematical groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, denoted Sp(2n, F) and Sp(n). The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually differing by factors of 2. The notation used here is consistent with the size of the matrices used to represent the groups. In Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
's classification of the simple Lie algebras, the Lie algebra of the complex group Sp(2n, C) is denoted Cn, and Sp(n) is the compact real form of Sp(2n, C).
The name "symplectic group" is due to Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
(details) as a replacement for the previous confusing names of (line) complex group and Abelian group, and is the Greek analog of "complex".
Sp(2n, F)
The symplectic group of degree 2n over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, denoted Sp(2n, F), is the group of 2n by 2n symplectic matrices with entries in F, and with the group operation that of matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. Since all symplectic matrices have determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1, the symplectic group is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2n, F).
More abstractly, the symplectic group can be defined as the set of linear transformations of a 2n-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over F that preserve a nondegenerate, skew-symmetric, bilinear form. Such a vector space is called a symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
. The symplectic group of an abstract symplectic vector space V is also denoted Sp(V).
When n = 1, the symplectic condition on a matrix is satisfied if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the determinant is one, so that Sp(2, F) = SL(2, F). For n > 1, there are additional conditions, i.e. Sp(2n, F) is then a proper subgroup of SL(2n, F).
Typically, the field F is the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, R, or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, C. In this case Sp(2n, F) is a real/complex Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of real/complex dimension n(2n + 1). These groups are connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
but noncompact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Sp(2n, C) is simply connected while Sp(2n, R) has a fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to Z.
The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of Sp(2n, F) is given by the set of 2n×2n matrices A (with entries in F) that satisfy
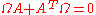
where
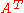is the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of A and Ω is the skew-symmetric matrix
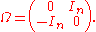
Sp(n)
The compact symplectic group, Sp(n), is the subgroup of GL(n, H) (invertible quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic matrices) which preserves the standard hermitian form on Hn:
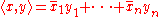
That is, Sp(n) is just the quaternionic unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
, U(n, H). Indeed, it is sometimes called the hyperunitary group. Also Sp(1) is the group of quaternions of unit 1, equivalent to SU(2) and topologically a 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
S3.
Note that Sp(n) is not a symplectic group in the sense of the previous section—it does not preserve a non-degenerate skew-symmetric (H-bilinear) form on Hn (in fact, the only skew-symmetric form is the zero form).
Rather, it is isomorphic to a subgroup of Sp(2n,C), and so does preserve a complex symplectic form in a vector space of dimension twice as high.
As explained below, the Lie algebra of Sp(n) is a real form of the complex symplectic Lie algebra sp(2n, C).
Sp(n) is a real Lie group with (real) dimension n(2n + 1). It is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, and simply connected. It can be defined by the intersection Sp(n)=U(2n) ∩ Sp(2n, C), where U(2n) stands for the unitary group.
The Lie algebra of Sp(n) is given by the quaternionic skew-Hermitian
Skew-Hermitian
An anti-Hermitian, skew-Hermitian, or skew-adjoint operator or matrix is one whose adjoint is the negative of itself:A^*=-A \, Imaginary numbers can be thought of as skew-adjoint , whereas real numbers correspond to self-adjoint operators....
matrices, the set of n by n quaternionic matrices that satisfy
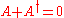
where
is the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A (here one takes the quaternionic conjugate). The Lie bracket is given by the commutator.
Relationships between the symplectic groups
The relationship between the groups Sp(2n, C), Sp(2n, R) and Sp(n) is most evident at the level of their Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s. It turns out that the first of these Lie algebras is a complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of the Lie algebras of either of the latter two groups.
Stated slightly differently, the complex Lie algebra sp(2n, C) of the complex Lie group Sp(2n, C) has several different real forms:
- the compact formCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, sp(n), which is the Lie algebra of Sp(n), - the algebras, sp(p, n − p), which are the Lie algebras of Sp(p, n − p), the indefinite signatureMetric signatureThe signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
equivalent to the compact form, - the normal formNormal formNormal form may refer to:* Normal form * Normal form * Normal form * Normal form In formal language theory:* Beta normal form* Chomsky normal form* Greibach normal form* Kuroda normal form...
(or split form), sp(2n, R), which is the Lie algebra of Sp(2n, R).
Important subgroups
The symplectic group Sp(n) is sometimes written as USp(2n) which is convenient for the following equations. The symplectic group comes up in quantum physics as a symmetry on poisson brackets so it is important to understand its subgroups. Some main subgroups are:
The symplectic groups are also subgroups of various Lie groups:
There are also the isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s of the Lie algebras usp(4) = o(5) and usp(2) = o(3) = su(2).
See also
- Orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
- Unitary groupUnitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
- Projective unitary groupProjective unitary groupIn mathematics, the projective unitary group PU is the quotient of the unitary group U by the right multiplication of its center, U, embedded as scalars....
- Symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
, Symplectic matrix, Symplectic vector spaceSymplectic vector spaceIn mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
, Symplectic representationSymplectic representationIn mathematical field of representation theory, a quaternionic representation is a representation on a complex vector space V with an invariant quaternionic structure, i.e., an antilinear equivariant mapj\colon V\to V\,which satisfiesj^2=-1.\,... - Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
- Θ10Θ10In representation theory, a branch of mathematics, θ10 is a cuspidal unipotent complex irreducible representation of the symplectic group Sp4 over a finite, local, or global field....