Home Discussion Topics Dictionary Almanac

Signup Login

Tangent bundle

Discussion

Ask a question about 'Tangent bundle'

Start a new discussion about 'Tangent bundle'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In differential geometry, the tangent bundle of a differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

M is the disjoint union

Disjoint union

In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...

The disjoint union assures that for any two points x₁ and x₂ of manifold M the tangent spaces T₁ and T₂ have no common vector. This is graphically illustrated in the accompanying picture for tangent bundle of circle S¹, see Examples section: all tangents to a circle lie in the plane of the circle. In order to make them disjoint it is necessary to align them in a plane perpendicular to the plane of the circle. of the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

s of M. That is,

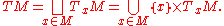
where T_xM denotes the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

to M at the point x. So, an element of TM can be thought of as a pair

Ordered pair

In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...

(x, v), where x is a point in M and v is a tangent vector to M at x. There is a natural projection

Projection (mathematics)

Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...

defined by π(x, v) = x. This projection maps each tangent space T_xM to the single point x.

The tangent bundle to a manifold is the prototypical example of a vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

(a fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

whose fibers are vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s). A section

Section (fiber bundle)

In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...

of TM is a vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

on M, and the dual bundle

Dual bundle

In mathematics, the dual bundle of a vector bundle π : E → X is a vector bundle π* : E* → X whose fibers are the dual spaces to the fibers of E...

to TM is the cotangent bundle

Cotangent bundle

In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...

, which is the disjoint union of the cotangent space

Cotangent space

In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...

s of M. By definition, a manifold M is parallelizable if and only if the tangent bundle is trivial.
By definition, a manifold M is framed if and only if the tangent bundle TM is stably trivial, meaning that for some trivial bundle E the Whitney sum

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

is trivial. For example, the n-dimensional sphere Sⁿ is framed for all n, but parallelizable only for n=1,3,7 (by results of Bott-Milnor and Kervaire).

Role

The main role of the tangent bundle is to provide a domain and range for the derivative of a smooth function. Namely, if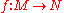

is a smooth function, with

and

smooth manifolds, its derivative

Derivative (generalizations)

The derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, and geometry.- Derivatives in analysis :...

is a smooth function

.

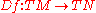Topology and smooth structure

The tangent bundle comes equipped with a natural topology (not the disjoint union topology) and smooth structure

Smooth structure

In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....

so as to make it into a manifold in its own right. The dimension of TM is twice the dimension of M.

Each tangent space of an n-dimensional manifold is an n-dimensional vector space. If U is an open contractible

Contractible space

In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....

subset of M, then there is a diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

from TU to U × Rⁿ which restricts to a linear isomorphism from each tangent space T_xU to {x}× Rⁿ . As a manifold, however, TM is not always diffeomorphic to the product manifold M × Rⁿ. When it is of the form M × Rⁿ, then the tangent bundle is said to be trivial. Trivial tangent bundles usually occur for manifolds equipped with a 'compatible group structure'; for instance, in the case where the manifold is a Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

. The tangent bundle of the unit circle is trivial because it is a Lie group (under multiplication and its natural differential structure). It is not true however that all spaces with trivial tangent bundles are Lie groups; manifolds which have a trivial tangent bundle are called parallelizable. Just as manifolds are locally modelled on Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, tangent bundles are locally modelled on U × Rⁿ, where U is an open subset of Euclidean space.

If M is a smooth n-dimensional manifold, then it comes equipped with an atlas

Atlas (topology)

In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...

of charts (U_α, φ_α) where U_α is an open set in M and

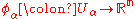
is a diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

. These local coordinates on U give rise to an isomorphism between T_xM and Rⁿ for each x ∈ U. We may then define a map

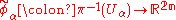
by

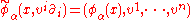
We use these maps to define the topology and smooth structure on TM. A subset A of TM is open if and only if

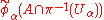is open in R²ⁿ for each α. These maps are then homeomorphisms between open subsets of TM and R²ⁿ and therefore serve as charts for the smooth structure on TM. The transition functions on chart overlaps

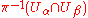are induced by the Jacobian matrices of the associated coordinate transformation and are therefore smooth maps between open subsets of R²ⁿ.

The tangent bundle is an example of a more general construction called a vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

(which is itself a specific kind of fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

). Explicitly, the tangent bundle to an n-dimensional manifold M may be defined as a rank n vector bundle over M whose transition functions are given by the Jacobian

Jacobian

In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...

of the associated coordinate transformations.

Examples

The simplest example is that of Rⁿ. In this case the tangent bundle is trivial.

Another simple example is the unit circle

Unit circle

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...

, S¹ (see picture above). The tangent bundle of the circle is also trivial and isomorphic to S¹ × R. Geometrically, this is a cylinder

Cylinder (geometry)

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

of infinite height (see the bottom picture).

The only tangent bundles that can be readily visualized are those of the real line R and the unit circle S¹, both of which are trivial. For 2-dimensional manifolds the tangent bundle is 4-dimensional and hence difficult to visualize.

A simple example of a nontrivial tangent bundle is that of the unit sphere S²: this tangent bundle is nontrivial as a consequence of the hairy ball theorem

Hairy ball theorem

The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...

. Therefore, the sphere is not parallelizable.

Vector fields

A smooth assignment of a tangent vector to each point of a manifold is called a vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

. Specifically, a vector field on a manifold M is a smooth map

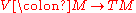
such that the image of x, denoted V_x, lies in T_xM, the tangent space at x. In the language of fiber bundles, such a map is called a section

Section (fiber bundle)

In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...

. A vector field on M is therefore a section of the tangent bundle of M.

The set of all vector fields on M is denoted by Γ(TM). Vector fields can be added together pointwise

and multiplied by smooth functions on M

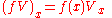
to get other vector fields. The set of all vector fields Γ(TM) then takes on the structure of a module

Module (mathematics)

In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...

over the commutative algebra

Commutative algebra

Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...

of smooth functions on M, denoted C^∞(M).

A local vector field on M is a local section of the tangent bundle. That is, a local vector field is defined only on some open set U in M and assigns to each point of U a vector in the associated tangent space. The set of local vector fields on M forms a structure known as a sheaf

Sheaf (mathematics)

In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...

of real vector spaces on M.

Higher-order tangent bundles

Since the tangent bundle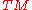

is itself a smooth manifold, the second-order tangent bundle

Double tangent bundle

In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...

can be defined via repeated application of the tangent bundle construction:

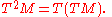
In general, the

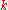th-order tangent bundle

can be defined recursively as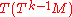

.

A smooth map

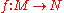has an induced derivative, for which the tangent bundle is the appropriate domain and range

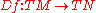. Similarly, higher-order tangent bundles provide the domain and range for higher-order derivatives

.

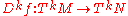A distinct but related construction are the jet bundle

Jet bundle

In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...

s on a manifold, which are bundles consisting of jets

Jet (mathematics)

In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...

.

Canonical vector field on tangent bundle

On every tangent bundle TM one can define a canonical vector field

. If (x, v) are local coordinates for TM, the vector field has the expression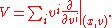

Alternatively, consider

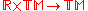to be the scalar multiplication function

. The derivative of this function with respect to the variable

at time

is a function

, which is an alternative description of the canonical vector field.

The existence of such a vector field on TM can be compared with the existence of a canonical 1-form on the cotangent bundle

Cotangent bundle

In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...

. Sometimes V is also called the Liouville vector field, or radial vector field. Using V one can characterize the tangent bundle. Essentially, V can be characterized using 4 axioms, and if a manifold has a vector field satisfying these axioms, then the manifold is a tangent bundle and the vector field is the canonical vector field on it. See for example, De León et al.

Lifts

There are various ways to lift objects on M into objects on TM. For example, if c is a curve in M, then c (the tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

of c) is a curve in TM. Let us point out that without further assumptions on M (say, a Riemannian metric), there is no similar lift into the cotangent bundle

Cotangent bundle

In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...

.

The vertical lift of a function

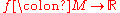
is the function

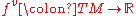defined by

, where

is the
canonical projection.

Tangent bundle

Role

Topology and smooth structure

Examples

Vector fields

Higher-order tangent bundles

Canonical vector field on tangent bundle

Lifts

See also

External links