Special linear group
Encyclopedia
In mathematics
, the special linear group of degree n over a field
F is the set of n×n matrices
with determinant
1, with the group operations of ordinary matrix multiplication
and matrix inversion.
This is the normal subgroup
of the general linear group
, given by the kernel
of the determinant
where we write F× for the multiplicative group of F (that is, excluding 0).
These elements are "special" in that they fall on a subvariety
of the general linear group – they satisfy a polynomial equation (since the determinant is polynomial in the entries).
and orientation
preserving linear transformations of Rn; this corresponds to the interpretation of the determinant as measuring change in volume and orientation.
of GL(n) of dimension n2 − 1. The Lie algebra
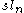of SL(n) consists of all n×n matrices over F with vanishing trace. The Lie bracket is given by the commutator
.
of the unitary matrix is on the unit circle
while that of the hermitian matrix is real and positive, and since in the case of a matrix from the special linear group the product of these two determinants must be 1, then each of them must be 1. Therefore, a special linear matrix can be written as the product of a special unitary matrix (or special orthogonal matrix in the real case) and a positive definite
hermitian matrix (or symmetric matrix in the real case) having determinant 1.
Thus the topology of the group SL(n, C) is the product
of the topology of SU(n) and the topology of the group of hermitian matrices of unit determinant with positive eigenvalues. A hermitian matrix of unit determinant and having positive eigenvalues can be uniquely expressed as the exponential
of a traceless hermitian matrix, and therefore the topology of this is that of n2-1 dimensional Euclidean space
.
The topology of SL(n, R) is the product of the topology of SO(n) and the topology of the group of symmetric matrices with positive eigenvalues. Since the latter matrices can be uniquely expressed as the exponential of symmetric traceless matrices, then this latter topology is that of (n+2)(n-1)/2 dimensional Euclidean space.
The group SL(n, C), like SU(n), is simply connected while SL(n, R), like SO(n), is not. SL(n, R) has the same fundamental group as GL+(n, R) or SO(n), that is, Z for n = 2 and Z2 for n > 2.
of GL, and the group generated by transvections. These are both subgroups of SL (transvections have determinant 1, and det is a map to an abelian group, so
), but in general do not coincide with it.
The group generated by transvections is denoted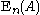
(for elementary matrices) or
. By the second Steinberg relation, for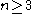 
, transvections are commutators, so
for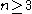
, 
.
For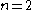
, transvections need not be commutators (of 2×2 matrices), as seen for example when 
is the field of two elements, then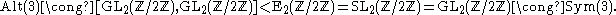
However, if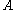
is a field, then 
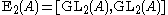unless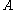 
is the field of two elements, and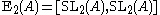
unless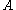 
is the field of 2 elements or the field of 3 elements.
In some circumstances these coincide: the special linear group over a field or a Euclidean domain
is generated by transvections, and the stable special linear group over a Dedekind domain
is generated by transvections. For more general rings the stable difference is measured by the special Whitehead group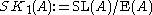
, where 
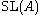and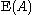 
are the stable group
s of the special linear group and elementary matrices.
or Euclidean domain
), one can give a presentation
of SL using transvections with some relations. Transvections satisfy the Steinberg relations, but these are not sufficient: the resulting group is the Steinberg group
, which is not the special linear group, but rather the universal central extension of the commutator subgroup of GL.
A sufficient set of relations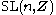 for
for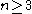 
is given by two of the Steinberg relations, plus a third relation .
Let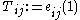
be the elementary matrix with 1's on the diagonal and in the 
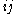position, and 0's elsewhere (and 
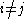). Then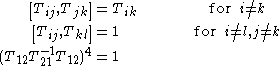
are a complete set of relations for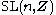
, 
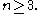
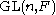splits over its determinant (we use 
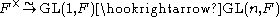as the monomorphism
from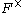
to 
,
see semidirect product
), and therefore GL(n, F) can be written as a semidirect product
of SL(n, F) by F×:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the special linear group of degree n over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is the set of n×n matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1, with the group operations of ordinary matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and matrix inversion.
This is the normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, given by the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the determinant
where we write F× for the multiplicative group of F (that is, excluding 0).
These elements are "special" in that they fall on a subvariety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of the general linear group – they satisfy a polynomial equation (since the determinant is polynomial in the entries).
Geometric interpretation
The special linear group SL(n, R) can be characterized as the group of volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
preserving linear transformations of Rn; this corresponds to the interpretation of the determinant as measuring change in volume and orientation.
Lie subgroup
When F is R or C, SL(n) is a Lie subgroupLie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of GL(n) of dimension n2 − 1. The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
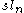of SL(n) consists of all n×n matrices over F with vanishing trace. The Lie bracket is given by the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
.
Topology
Any invertible matrix can be uniquely represented according to the polar decomposition as the product of a unitary matrix and a hermitian matrix with positive eigenvalues. The determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the unitary matrix is on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
while that of the hermitian matrix is real and positive, and since in the case of a matrix from the special linear group the product of these two determinants must be 1, then each of them must be 1. Therefore, a special linear matrix can be written as the product of a special unitary matrix (or special orthogonal matrix in the real case) and a positive definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
hermitian matrix (or symmetric matrix in the real case) having determinant 1.
Thus the topology of the group SL(n, C) is the product
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of the topology of SU(n) and the topology of the group of hermitian matrices of unit determinant with positive eigenvalues. A hermitian matrix of unit determinant and having positive eigenvalues can be uniquely expressed as the exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
of a traceless hermitian matrix, and therefore the topology of this is that of n2-1 dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
The topology of SL(n, R) is the product of the topology of SO(n) and the topology of the group of symmetric matrices with positive eigenvalues. Since the latter matrices can be uniquely expressed as the exponential of symmetric traceless matrices, then this latter topology is that of (n+2)(n-1)/2 dimensional Euclidean space.
The group SL(n, C), like SU(n), is simply connected while SL(n, R), like SO(n), is not. SL(n, R) has the same fundamental group as GL+(n, R) or SO(n), that is, Z for n = 2 and Z2 for n > 2.
Relations to other subgroups of GL(n,A)
Two related subgroups, which in some cases coincide with SL, and in other cases are accidentally conflated with SL, are the commutator subgroupCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of GL, and the group generated by transvections. These are both subgroups of SL (transvections have determinant 1, and det is a map to an abelian group, so
), but in general do not coincide with it.The group generated by transvections is denoted
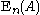
(for elementary matrices) or
. By the second Steinberg relation, for 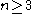, transvections are commutators, sofor
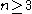, .For
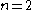, transvections need not be commutators (of 2×2 matrices), as seen for example when is the field of two elements, then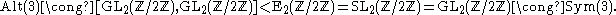However, if
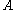is a field, then 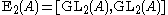unless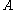 is the field of two elements, and
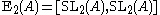unless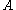 is the field of 2 elements or the field of 3 elements.
In some circumstances these coincide: the special linear group over a field or a Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
is generated by transvections, and the stable special linear group over a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
is generated by transvections. For more general rings the stable difference is measured by the special Whitehead group
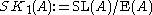, where 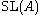and 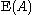are the stable groupDirect limit of groups
In mathematics, a direct limit of groups is the direct limit of a direct system of groups. These are central objects of study in algebraic topology, especially stable homotopy theory and homological algebra...
s of the special linear group and elementary matrices.
Generators and relations
If working over a ring where SL is generated by transvections (such as a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
or Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
), one can give a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
of SL using transvections with some relations. Transvections satisfy the Steinberg relations, but these are not sufficient: the resulting group is the Steinberg group
Steinberg group
In mathematics, Steinberg group means either of two distinct, though related, constructions of the mathematician Robert Steinberg:*Steinberg group St in algebraic K-theory.*Steinberg group is a 'twisted' group of Lie type....
, which is not the special linear group, but rather the universal central extension of the commutator subgroup of GL.
A sufficient set of relations 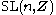for
for 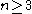is given by two of the Steinberg relations, plus a third relation .Let
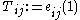be the elementary matrix with 1's on the diagonal and in the 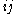position, and 0's elsewhere (and 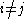). Then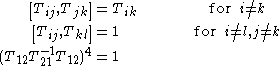are a complete set of relations for
, Structure of GL(n,F)
The group splits over its determinant (we use 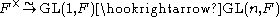as the monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
from
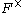to ,see semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
), and therefore GL(n, F) can be written as a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of SL(n, F) by F×:
- GL(n, F) = SL(n, F) ⋊ F×.
See also
- SL2(R)
- SL2(C)
- Modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
- Projective linear groupProjective linear groupIn mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...