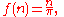.gif)
Function (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function associates one quantity, the argument
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
of the function, also known as the input, with another quantity, the value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, but they can also be elements from any given set. A function f with argument x is denoted f(x), which is read "f of x". An example of such a function is f(x) = 2x, the function which associates with every number x the number twice as large. For instance, if its argument is 5 its value is 10, and this is written f(5) = 10.
The input to a function need not be a number, it can be any well defined object. For example, a function might associate the letter A with the number 1, the letter B with the number 2, and so on. There are many ways to describe or represent a function, such as a formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
or algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that computes the output for a given input, a graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
that gives a picture of the function, or a table of values that gives the output for certain specified inputs. Tables of values are especially common in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
.
The set of all inputs to a particular function is called its domain. The set of all outputs of a particular function is called its image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
. In modern mathematics functions also have a codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
. For every function, its codomain includes its image. For instance, a codomain of the function squaring real numbers
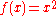 usually is defined to be the set of all real numbers. The function
usually is defined to be the set of all real numbers. The function  does not have the real numbers
does not have the real numbers  as outputs, thus they are in its codomain but not in its image. Codomains are useful for function composition
as outputs, thus they are in its codomain but not in its image. Codomains are useful for function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. Composition
 (
(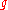 followed by
followed by  ) is defined if the codomain of
) is defined if the codomain of  is the same as the domain of
is the same as the domain of  . Thus the codomain of
. Thus the codomain of  defines what functions may follow
defines what functions may follow 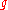 . The word range
. The word rangeRange (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is used in some texts to refer to the image and in others to the codomain, in particular in computing it often refers to the codomain. The domain and codomain are often "understood." Thus for the example given above, f(x) = 2x, the domain and codomain were not stated explicitly. They might both be the set of all real numbers, but they might also be the set of integers. If the domain is the set of integers, then image consists of just the even integers.
The set of all the ordered pairs or inputs and outputs (x, f(x)) of a function is called its graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
. A common way to define a function is as the triple (domain, codomain, graph), that is as the input set, the possible outputs and the mapping for each input to its output.
A function may sometimes be described through its relationship to other functions, for example, as the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of a given function, or as a solution of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
. Functions can be added, multiplied, or combined in other ways to produce new functions. An important operation on functions, which distinguishes them from number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s, is the composition of functions. There are uncountably many
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
different functions, most of which cannot be expressed with a formula or an algorithm.
Collections of functions with certain properties, such as continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s and differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s, are called function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s and are studied as objects in their own right, in such mathematical disciplines as real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
and complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
.
Overview
Because functions are so widely used, many traditions have grown up around their use. The symbol for the input to a function is often called the independent variableIndependent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
or argument and is often represented by the letter x or, if the input is a particular time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, by the letter t. The symbol for the output is called the dependent variable or value and is often represented by the letter y. The function itself is most often called f, and thus the notation y = f(x) indicates that a function named f has an input named x and an output named y.
The set of all permitted inputs to a given function is called the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of the function. The set of all resulting outputs is called the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
or range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of the function. The image is often a subset of some larger set, called the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of a function. Thus, for example, the function f(x) = x2 could take as its domain the set of all real numbers, as its image the set of all non-negative real numbers, and as its codomain the set of all real numbers. In that case, we would describe f as a real-valued function of a real variable. Sometimes, especially in computer science
Range (computer science)
In computer science, the term range may refer to one of three things:# The possible values that may be stored in a variable.# The upper and lower bounds of an array.# An alternative to iterator.-Range of a variable:...
, the term "range" refers to the codomain rather than the image, so care needs to be taken when using the word.
It is usual practice in mathematics to introduce functions with temporary names like ƒ. For example, ƒ(x) = 2x+1, implies ƒ(3) = 7; when a name for the function is not needed, the form y = may be used. If a function is often used, it may be given a more permanent name as, for example,

Functions need not act on numbers: the domain and codomain of a function may be arbitrary sets. One example of a function that acts on non-numeric inputs takes English words as inputs and returns the first letter of the input word as output. Furthermore, functions need not be described by any expression, rule or algorithm: indeed, in some cases it may be impossible to define such a rule. For example, the association between inputs and outputs in a choice function often lacks any fixed rule, although each input element is still associated to one and only one output.
A function of two or more variables is considered in formal mathematics as having a domain consisting of ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s or tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of the argument values. For example Sum(x,y) = x+y operating on integers is the function Sum with a domain consisting of pairs of integers. Sum then has a domain consisting of elements like (3,4), a codomain of integers, and an association between the two that can be described by a set of ordered pairs like ((3,4), 7). Evaluating Sum(3,4) then gives the value 7 associated with the pair (3,4).
A family of objects indexed by a set
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
is equivalent to a function. For example, the sequence 1, 1/2, 1/3, ..., 1/n, ... can be written as the ordered sequence <1/n> where n is a natural number, or as a function f(n) = 1/n from the set of natural numbers into the set of rational numbers.
Definition
One precise definition of a function is an ordered triple of sets, written (X, Y, F), where X is the domain, Y is the codomain, and F is a set of ordered pairs (a, b). In each of the ordered pairs, the first element a is from the domain, the second element b is from the codomain, and a necessary condition is that every element in the domain is the first element in exactly one ordered pair. The set of all b is known as the imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the function, and need not be the whole of the codomain. Most authors use the term "range" to mean the image, while some use "range" to mean the codomain.
The domain X may be void, but if X = ∅ then F = ∅. The codomain Y may be also void, but if Y = ∅ then X = ∅ and F = ∅. Such “void” functions
Empty function
In mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
are not usual, but the theory assures their existence.
The notation ƒ:X→Y indicates that ƒ is a function with domain X and codomain Y, and the function f is said to map or associate elements of X to elements of Y.
If the domain and codomain are both the set of real numbers, using the ordered triple scheme we can, for example, write the function
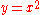 as
as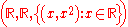 ,
,In most situations, the domain and codomain are understood from context, and only the relationship between the input and output is given.
In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
especially, a function f is often defined as a set of ordered pairs, with the property that if
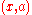 and
and 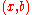 are in f, then
are in f, then  . In this case statements such as
. In this case statements such as 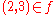 are appropriate when, say,
are appropriate when, say,  is defined by
is defined by 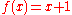 , for all
, for all 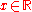 .
.The graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of a function is its set of ordered pairs. Part of such a set can be plotted on a pair of coordinate axes; for example, (3, 9), the point above 3 on the horizontal axis and to the right of 9 on the vertical axis, lies on the graph of
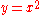 .
.A specific input in a function is called an argument of the function. For each argument value x, the corresponding unique y in the codomain is called the function value at x, output of ƒ for an argument x, or the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of x under ƒ. The image of x may be written as ƒ(x) or as y.
A function can also be called a map or a mapping. Some authors, however, use the terms "function" and "map" to refer to different types of functions. Other specific types of functions include functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s and operators.
A function is a special case of a more general mathematical concept, the relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, for which the restriction that each element of the domain appear as the first element in one and only one ordered pair is removed. In other words, an element of the domain may not be the first element of any ordered pair, or may be the first element of two or more ordered pairs. A relation is "single-valued" when if an element of the domain is the first element of one ordered pair, it is not the first element of any other ordered pair. A relation is "left-total" or simply "total" if every element of the domain is the first element of some ordered pair. Thus a function is a total, single-valued relation.
In some parts of mathematics, including recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, it is convenient to study partial functions in which some values of the domain have no association in the graph; i.e., single-valued relations. For example, the function f such that f(x) = 1/x does not define a value for x = 0, and so is only a partial function from the real line to the real line. The term total function can be used to stress the fact that every element of the domain does appear as the first element of an ordered pair in the graph. In other parts of mathematics, non-single-valued relations are similarly conflated with functions: these are called multivalued function
Multivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
s, with the corresponding term single-valued function
Single-valued function
A single-valued function is an emphatic term for a mathematical function in the usual sense. That is, each element of the function's domain maps to a single, well-defined element of its range. This contrasts with a general binary relation, which can be viewed as being a multi-valued function...
for ordinary functions.
Many operations in set theory, such as the power set, have the class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all sets as their domain, and therefore, although they are informally described as functions, they do not fit the set-theoretical definition outlined above, because a class is not necessarily a set.
Notation
Formal description of a function typically involves the function's name, its domain, its codomain, and a rule of correspondence. Thus we frequently see a two-part notation, an example being-

where the first part is read:- "ƒ is a function from N to R" (one often writes informally "Let ƒ: X → Y" to mean "Let ƒ be a function from X to Y"), or
- "ƒ is a function on N into R", or
- "ƒ is an R-valued function of an N-valued variable",
and the second part is read:-
 maps to
maps to 
Here the function named "ƒ" has the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s as domain, the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s as codomain, and maps n to itself divided by π. Less formally, this long form might be abbreviated
where f(n) is read as "f as function of n" or "f of n". There is some loss of information: we no longer are explicitly given the domain N and codomain R.
It is common to omit the parentheses around the argument when there is little chance of confusion, thus: sin x; this is known as prefix notation. Writing the function after its argument, as in x ƒ, is known as postfix notation; for example, the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function is customarily written n!, even though its generalization, the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, is written Γ(n). Parentheses are still used to resolve ambiguities and denote precedence, though in some formal settings the consistent use of either prefix or postfix notation eliminates the need for any parentheses.
Injective and surjective functions
Three important kinds of function are the injectionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
s (or one-to-one functions), which have the property that if ƒ(a) = ƒ(b) then a must equal b; the surjections (or onto functions), which have the property that for every y in the codomain there is an x in the domain such that ƒ(x) = y; and the bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s, which are both one-to-one and onto. This nomenclature was introduced by the Bourbaki groupNicolas BourbakiNicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
.
When the definition of a function by its graph only is used, since the codomain is not defined, the "surjection" must be accompanied with a statement about the set the function maps onto. For example, we might say ƒ maps onto the set of all real numbers.
Functions with multiple inputs and outputs
The concept of function can be extended to an object that takes a combination of two (or more) argument values to a single result. This intuitive concept is formalized by a function whose domain is the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two or more sets.
For example, consider the function that associates two integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s to their product: ƒ(x, y) = x·y. This function can be defined formally as having domain Z×Z , the set of all integer pairs; codomain Z; and, for graph, the set of all pairs ((x,y), x·y). Note that the first component of any such pair is itself a pair (of integers), while the second component is a single integer.
The function value of the pair (x,y) is ƒ((x,y)). However, it is customary to drop one set of parentheses and consider ƒ(x,y) a function of two variables, x and y. Functions of two variables may be plotted on the three-dimensional Cartesian as ordered triples of the form (x,y,f(x,y)).
The concept can still further be extended by considering a function that also produces output that is expressed as several variables. For example, consider the integer divide function, with domain Z×N and codomain Z×N. The resultant (quotient, remainder) pair is a single value in the codomain seen as a Cartesian product.
Currying
An alternative approach to handling functions with multiple arguments is to transform them into a chain of functions that each takes a single argument. For instance, one can interpret Add(3,5) to mean "first produce a function that adds 3 to its argument, and then apply the 'Add 3' function to 5". This transformation is called curryingCurryingIn mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
: Add 3 is curry(Add) applied to 3. There is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the function spaces CA×B and (CB)A.
When working with curried functions it is customary to use prefix notation with function application considered left-associative, since juxtaposition of multiple arguments—as in (ƒ x y)—naturally maps to evaluation of a curried function. Conversely, the → and ⟼ symbols are considered to be right-associative, so that curried functions may be defined by a notation such as ƒ: Z → Z → Z = x ⟼ y ⟼ x·y
Binary operations
The familiar binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s of arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, can be viewed as functions from R×R to R. This view is generalized in abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, where n-ary functions are used to model the operations of arbitrary algebraic structures. For example, an abstract groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is defined as a set X and a function ƒ from X×X to X that satisfies certain properties.
Traditionally, addition and multiplication are written in the infixInfixAn infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
notation: x+y and x×y instead of +(x, y) and ×(x, y).
Function composition
The function composition of two or more functions takes the output of one or more functions as the input of others. The functions ƒ: X → Y and g: Y → Z can be composed by first applying ƒ to an argument x to obtain y = ƒ(x) and then applying g to y to obtain z = g(y). The composite function formed in this way from general ƒ and g may be written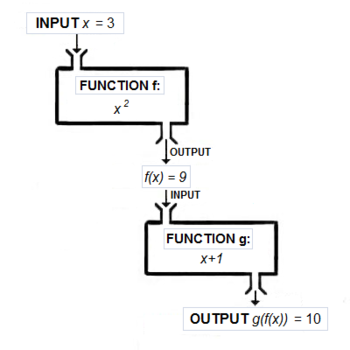
-
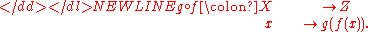
This notation follows the form such that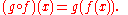
The function on the right acts first and the function on the left acts second, reversing English reading order. We remember the order by reading the notation as "g of ƒ". The order is important, because rarely do we get the same result both ways. For example, suppose ƒ(x) = x2 and g(x) = x+1. Then g(ƒ(x)) = x2+1, while ƒ(g(x)) = (x+1)2, which is x2+2x+1, a different function.
In a similar way, the function given above by the formula y = 5x−20x3+16x5 can be obtained by composing several functions, namely the additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, negationNegation (algebra)Negation is the mathematical operation that reverses the sign of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero is zero...
, and multiplication of real numbers.
An alternative to the colon notation, convenient when functions are being composed, writes the function name above the arrow. For example, if ƒ is followed by g, where g produces the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
eix, we may write
A more elaborate form of this is the commutative diagramCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
.
Identity function
The unique function over a set X that maps each element to itself is called the identity function for X, and typically denoted by idX. Each set has its own identity function, so the subscript cannot be omitted unless the set can be inferred from context. Under composition, an identity function is "neutral": if ƒ is any function from X to Y, then
Restrictions and extensions
Informally, a restriction of a function ƒ is the result of trimming its domain.
More precisely, if ƒ is a function from a X to Y, and S is any subset of X, the restriction of ƒ to S is the function ƒ|S from S to Y such that ƒ|S(s) = ƒ(s) for all s in S.
If g is a restriction of ƒ, then it is said that ƒ is an extension of g.
The overriding of f: X → Y by g: W → Y (also called overriding union) is an extension of g denoted as (f ⊕ g): (X ∪ W) → Y. Its graph is the set-theoretical union of the graphs of g and f|X \ W. Thus, it relates any element of the domain of g to its image under g, and any other element of the domain of f to its image under f. Overriding is an associative operation; it has the empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
as an identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. If f|X ∩ W and g|X ∩ W are pointwise equal (e.g., the domains of f and g are disjoint), then the union of f and g is defined and is equal to their overriding union. This definition agrees with the definition of union for binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s.
Inverse function
If ƒ is a function from X to Y then an inverse function for ƒ, denoted by ƒ−1, is a function in the opposite direction, from Y to X, with the property that a round trip (a compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
) returns each element to itself. Not every function has an inverse; those that do are called invertible. The inverse function exists if and only if ƒ is a bijection.
As a simple example, if ƒ converts a temperature in degrees Celsius C to degrees Fahrenheit F, the function converting degrees Fahrenheit to degrees Celsius would be a suitable ƒ−1.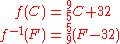
The notation for composition is similar to multiplication; in fact, sometimes it is denoted using juxtaposition, gƒ, without an intervening circle. With this analogy, identity functions are like the multiplicative identity, 1, and inverse functions are like reciprocalsMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
(hence the notation).
For functions that are injections or surjections, generalized inverse functions can be defined, called left and right inverses respectively. Left inverses map to the identity when composed to the left; right inverses when composed to the right.
Image of a set
The concept of the image can be extended from the image of a point to the image of a set. If A is any subset of the domain, then ƒ(A) is the subset of im ƒ consisting of all images of elements of A. We say the ƒ(A) is the image of A under f.
Use of ƒ(A) to denote the image of a subset A⊆X is consistent so long as no subset of the domain is also an element of the domain. In some fields (e.g., in set theory, where ordinalsOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
are also sets of ordinals) it is convenient or even necessary to distinguish the two concepts; the customary notation is ƒ[A] for the set { ƒ(x): x ∈ A }.
Notice that the image of ƒ is the image ƒ(X) of its domain, and that the image of ƒ is a subset of its codomain.
Inverse image
The inverse image (or preimage, or more precisely, complete inverse image) of a subset B of the codomain Y under a function ƒ is the subset of the domain X defined by
So, for example, the preimage of {4, 9} under the squaring function is the set {−3,−2,2,3}.
In general, the preimage of a singleton set (a set with exactly one element) may contain any number of elements. For example, if ƒ(x) = 7, then the preimage of {5} is the empty set but the preimage of {7} is the entire domain. Thus the preimage of an element in the codomain is a subset of the domain. The usual convention about the preimage of an element is that ƒ−1(b) means ƒ−1({b}), i.e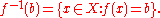
In the same way as for the image, some authors use square brackets to avoid confusion between the inverse image and the inverse function. Thus they would write ƒ−1[B] and ƒ−1[b] for the preimage of a set and a singleton.
The preimage of a singleton set is sometimes called a fiber. The term kernel can refer to a number of related concepts.
Specifying a function
A function can be defined by any mathematical condition relating each argument to the corresponding output value. If the domain is finite, a function ƒ may be defined by simply tabulating all the arguments x and their corresponding function values ƒ(x). More commonly, a function is defined by a formulaFormulaIn mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
, or (more generally) an algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
— a recipe that tells how to compute the value of ƒ(x) given any x in the domain.
There are many other ways of defining functions. Examples include piecewise definitions, induction or recursionRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, algebraic or analyticAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
, limitsLimit (mathematics)In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, analytic continuationAnalytic continuationIn complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
, infinite seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, and as solutions to integralIntegral equationIn mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
and differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. The lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
provides a powerful and flexible syntaxSyntaxIn linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
for defining and combining functions of several variables.
Computability
Functions that send integers to integers, or finite strings to finite strings, can sometimes be defined by an algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, which gives a precise description of a set of steps for computing the output of the function from its input. Functions definable by an algorithm are called computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s. For example, the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
gives a precise process to compute the greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of two positive integers. Many of the functions studied in the context of number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
are computable.
Fundamental results of computability theoryComputability theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
show that there are functions that can be precisely defined but are not computable. Moreover, in the sense of cardinality, almost all functions from the integers to integers are not computable. The number of computable functions from integers to integers is countable, because the number of possible algorithms is. The number of all functions from integers to integers is higher: the same as the cardinality of the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. Thus most functions from integers to integers are not computable. Specific examples of uncomputable functions are known, including the busy beaver function and functions related to the halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
and other undecidable problems.
Function spaces
The set of all functions from a set X to a set Y is denoted by X → Y, by [X → Y], or by YX.
The latter notation is motivated by the fact that, when X and Y are finite and of size |X| and |Y|, then the number of functions X → Y is |YX| = |Y||X|. This is an example of the convention from enumerative combinatorics that provides notations for sets based on their cardinalities. Other examples are the multiplication sign X×Y used for the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, where |X×Y| = |X|·|Y|; the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
sign X!, used for the set of permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s where |X!| = |X|!; and the binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
sign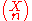 , used for the set of n-element subsets where
, used for the set of n-element subsets where 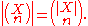
If ƒ: X → Y, it may reasonably be concluded that ƒ ∈ [X → Y].
Pointwise operations
Pointwise operations inherit properties from the corresponding operations on the codomain. For example if ƒ: X → R and g: X → R are functions with a common domain of X and common codomain of a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, then the sum function ƒ + g: X → R and the product function ƒ ⋅ g: X → R can be defined as follows:
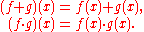
Other properties
There are many other special classes of functions that are important to particular branches of mathematics, or particular applications.
Here is a partial list:
- bijection, injection and surjectionBijection, injection and surjectionIn mathematics, injections, surjections and bijections are classes of functions distinguished by the manner in which arguments and images are related or mapped to each other.A function maps elements from its domain to elements in its codomain.*A function f: \; A \to B is injective...
, or singularly:- injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, - surjectiveSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
, and - bijective function
- injective
- continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
- differentiableDifferentiable functionIn calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
, integrable - linearLinear functionIn mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
, polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, rationalRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:... - algebraicAlgebraic functionIn mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
, transcendentalTranscendental functionA transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation... - trigonometric
- fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
- odd or evenEven and odd functionsIn mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
- convexConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, monotonicMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
, unimodal - holomorphicHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, meromorphicMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
, entireEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane... - vector-valuedVector-valued functionA vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
- computableComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
Functions prior to Leibniz
- Historically, some mathematicians can be regarded as having foreseen and come close to a modern formulation of the concept of function. Among them is Oresme (1323–1382) . . . In his theory, some general ideas about independent and dependent variable quantities seem to be present.
Ponte further notes that "The emergence of a notion of function as an individualized mathematical entity can be traced to the beginnings of infinitesimal calculusInfinitesimal calculusInfinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
".
The notion of "function" in analysis
As a mathematical term, "function" was coined by Gottfried LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, in a 1673 letter, to describe a quantity related to a curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
, such as a curve's slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
at a specific pointPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. The functions Leibniz considered are today called differentiable functionsDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. For this type of function, one can talk about limitLimit of a functionIn mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
s and derivatives; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
Johann BernoulliJohann BernoulliJohann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
"by 1718, had come to regard a function as any expression made up of a variable and some constants", and Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
during the mid-18th century used the word to describe an expressionExpression (mathematics)In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
or formulaFormulaIn mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
involving variables and constants e.g., .
Alexis Claude Clairaut (in approximately 1734) and Euler introduced the familiar notation " f(x) ".
At first, the idea of a function was rather limited. Joseph FourierJoseph FourierJean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
, for example, claimed that every function had a Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are nowhere differentiable. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
have shown that these functions are, in a precise sense, more common than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
.
During the 19th century, mathematicians started to formalize all the different branches of mathematics. WeierstrassKarl WeierstrassKarl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
advocated building calculus on arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
rather than on geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, which favoured Euler's definition over Leibniz's (see arithmetization of analysisArithmetization of analysisThe arithmetization of analysis was a research program in the foundations of mathematics carried out in the second half of the 19th century. Kronecker originally introduced the term arithmetization of analysis, by which he meant its constructivization in the context of the natural numbers...
).
DirichletJohann Peter Gustav Lejeune DirichletJohann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
and LobachevskyNikolai Ivanovich LobachevskyNikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...
are traditionally credited with independently giving the modern "formal" definition of a function as a relationRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
in which every first element has a unique second element. Eves asserts that "the student of mathematics usually meets the Dirichlet definition of function in his introductory course in calculus, but Dirichlet's claim to this formalization is disputed by Imre LakatosImre LakatosImre Lakatos was a Hungarian philosopher of mathematics and science, known for his thesis of the fallibility of mathematics and its 'methodology of proofs and refutations' in its pre-axiomatic stages of development, and also for introducing the concept of the 'research programme' in his...
:
- There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his
[1837] , for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function has two values: ...
In the context of "the Differential Calculus" George BooleGeorge BooleGeorge Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
defined (circa 1849) the notion of a function as follows:- "That quantity whose variation is uniform . . . is called the independent variable. That quantity whose variation is referred to the variation of the former is said to be a function of it. The Differential calculus enables us in every case to pass from the function to the limit. This it does by a certain Operation. But in the very Idea of an Operation is . . . the idea of an inverse operation. To effect that inverse operation in the present instance is the business of the Int[egral] Calculus."
The logician's "function" prior to 1850
Logicians of this time were primarily involved with analyzing syllogismSyllogismA syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
s (the 2000 year-old Aristotelian forms and otherwise), or as Augustus De MorganAugustus De MorganAugustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....
(1847) stated it: "the examination of that part of reasoning which depends upon the manner in which inferences are formed,
and the investigation of general maxims and rules for constructing arguments". At this time the notion of (logical) "function" is not explicit, but at least in the work of De Morgan and George BooleGeorge BooleGeorge Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
it is implied: we see abstraction of the argument forms, the introduction of variables, the introduction of a symbolic algebra with respect to these variables, and some of the notions of set theory.
De Morgan's 1847 "FORMAL LOGIC OR, The Calculus of Inference, Necessary and Probable" observes that "[a] logical truthLogical truthLogical truth is one of the most fundamental concepts in logic, and there are different theories on its nature. A logical truth is a statement which is true and remains true under all reinterpretations of its components other than its logical constants. It is a type of analytic statement.Logical...
depends upon the structure of the statement, and not upon the particular matters spoken of"; he wastes no time (preface page i) abstracting: "In the form of the proposition, the copula is made as absract as the terms". He immediately (p. 1) casts what he calls "the proposition" (present-day propositional function or relation) into a form such as "X is Y", where the symbols X, "is", and Y represent, respectively, the subject, copula, and predicate. While the word "function" does not appear, the notion of "abstraction" is there, "variables" are there, the notion of inclusion in his symbolism “all of the Δ is in the О” (p. 9) is there, and lastly a new symbolism for logical analysis of the notion of "relation" (he uses the word with respect to this example " X)Y " (p. 75) ) is there:- " A1 X)Y To take an X it is necessary to take a Y" [or To be an X it is necessary to be a Y]
- " A1 Y)X To take an Y it is sufficient to take a X" [or To be a Y it is sufficient to be an X], etc.
In his 1848 The Nature of Logic Boole asserts that "logic . . . is in a more especial sense the science of reasoning by signs", and he briefly discusses the notions of "belonging to" and "class": "An individual may possess a great variety of attributes and thus belonging to a great variety of different classes" . Like De Morgan he uses the notion of "variable" drawn from analysis; he gives an example of "represent[ing] the class oxen by x and that of horses by y and the conjunction and by the sign + . . . we might represent the aggregate class oxen and horses by x + y".
The logicians' "function" 1850–1950
Eves observes "that logicians have endeavored to push down further the starting level of the definitional development of mathematics and to derive the theory of sets, or classes, from a foundation in the logic of propositions and propositional functions". But by the late 19th century the logicians' research into the foundations of mathematics was undergoing a major split. The direction of the first group, the Logicists, can probably be summed up best by Bertrand Russell 1903:9 – "to fulfil two objects, first, to show that all mathematics follows from symbolic logic, and secondly to discover, as far as possible, what are the principles of symbolic logic itself."
The second group of logicians, the set-theorists, emerged with Georg CantorGeorg CantorGeorg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
's "set theory" (1870–1890) but were driven forward partly as a result of Russell's discovery of a paradox that could be derived from Frege's conception of "function", but also as a reaction against Russell's proposed solution. Zermelo's set-theoretic response was his 1908 Investigations in the foundations of set theory I – the first axiomatic set theory; here too the notion of "propositional function" plays a role.
George Boole's
The Laws of Thought 1854; John Venn's Symbolic Logic 1881 In his An Investigation into the laws of thought Boole now defined a function in terms of a symbol x as follows:- "8. Definition. – Any algebraic expression involving symbol
-
Boole then used algebraic expressions to define both algebraic and logical notions, e.g., 1−x is logical NOT(x), xy is the logical AND(x,y), x + y is the logical OR(x, y), x(x+y) is xx+xy, and "the special law" xx = x2 = x.
In his 1881 Symbolic Logic Venn was using the words "logical function" and the contemporary symbolism ( x = f(y), y = f−1(x), cf page xxi) plus the circle-diagrams historically associated with Venn to describe "class relations", the notions "'quantifying' our predicate", "propositions in respect of their extension", "the relation of inclusion and exclusion of two classes to one another", and "propositional function" (all on p. 10), the bar over a variable to indicate not-x (page 43), etc. Indeed he equated unequivocally the notion of "logical function" with "class" [modern "set"]: "... on the view adopted in this book, f(x) never stands for anything but a logical class. It may be a compound class aggregated of many simple classes; it may be a class indicated by certain inverse logical operations, it may be composed of two groups of classes equal to one another, or what is the same thing, their difference declared equal to zero, that is, a logical equation. But however composed or derived, f(x) with us will never be anything else than a general expression for such logical classes of things as may fairly find a place in ordinary Logic".
Frege's Begriffsschrift 1879
Gottlob FregeGottlob FregeFriedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
's BegriffsschriftBegriffsschriftBegriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
(1879) preceded Giuseppe PeanoGiuseppe PeanoGiuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
(1889), but Peano had no knowledge of Frege 1879 until after he had published his 1889. Both writers strongly influenced Bertrand RussellBertrand RussellBertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
(1903). Russell in turn influenced much of 20th-century mathematics and logic through his Principia MathematicaPrincipia MathematicaThe Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
(1913) jointly authored with Alfred North WhiteheadAlfred North WhiteheadAlfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
.
At the outset Frege abandons the traditional "concepts subject and predicate", replacing them with argument and function respectively, which he believes "will stand the test of time. It is easy to see how regarding a content as a function of an argument leads to the formation of concepts. Furthermore, the demonstration of the connection between the meanings of the words if, and, not, or, there is, some, all, and so forth, deserves attention".
Frege begins his discussion of "function" with an example: Begin with the expression "Hydrogen is lighter than carbon dioxide". Now remove the sign for hydrogen (i.e., the word "hydrogen") and replace it with the sign for oxygen (i.e., the word "oxygen"); this makes a second statement. Do this again (using either statement) and substitute the sign for nitrogen (i.e., the word "nitrogen") and note that "This changes the meaning in such a way that "oxygen" or "nitrogen" enters into the relations in which "hydrogen" stood before". There are three statements:- "Hydrogen is lighter than carbon dioxide."
- "Oxygen is lighter than carbon dioxide."
- "Nitrogen is lighter than carbon dioxide."
Now observe in all three a "stable component, representing the totality of [the] relations"; call this the function, i.e.,- "... is lighter than carbon dioxide", is the function.
Frege calls the argument of the function "[t]he sign [e.g., hydrogen, oxygen, or nitrogen], regarded as replaceable by others that denotesDenotationThis word has distinct meanings in other fields: see denotation . For the opposite of Denotation see Connotation.*In logic, linguistics and semiotics, the denotation of a word or phrase is a part of its meaning; however, the part referred to varies by context:** In grammar and literary theory, the...
the object standing in these relations". He notes that we could have derived the function as "Hydrogen is lighter than . . .." as well, with an argument position on the right; the exact observation is made by Peano (see more below). Finally, Frege allows for the case of two (or more arguments). For example, remove "carbon dioxide" to yield the invariant part (the function) as:- "... is lighter than ... "
The one-argument function Frege generalizes into the form Φ(A) where A is the argument and Φ represents the function, whereas the two-argument function he symbolizes as Ψ(A, B) with A and B the arguments and Ψ( ) the function and cautions that "in general Ψ(A, B) differs from Ψ(B, A)". Using his unique symbolism he translates for the reader the following symbolism:- "We can read |--- Φ(A) as "A has the property Φ. |--- Ψ(A, B) can be translated by "B stands in the relation Ψ to A" or "B is a result of an application of the procedure Ψ to the object A".
Peano 1889 The Principles of Arithmetic 1889
Peano defined the notion of "function" in a manner somewhat similar to Frege, but without the precision. First Peano defines the sign "K means class, or aggregate of objects", the objects of which satisfy three simple equality-conditions, a = a, (a = b) = (b = a), IF ((a = b) AND (b = c)) THEN (a = c). He then introduces φ, "a sign or an aggregate of signs such that if x is an object of the class s, the expression φx denotes a new object". Peano adds two conditions on these new objects: First, that the three equality-conditions hold for the objects φx; secondly, that "if x and y are objects of class s and if x = y, we assume it is possible to deduce φx = φy". Given all these conditions are met, φ is a "function presign". Likewise he identifies a "function postsign". For example if φ is the function presign a+, then φx yields a+x, or if φ is the function postsign +a then xφ yields x+a.
Bertrand Russell's
The Principles of Mathematics 1903 While the influence of Cantor and Peano was paramount, in Appendix A "The Logical and Arithmetical Doctrines of Frege" of The Principles of MathematicsThe Principles of MathematicsThe Principles of Mathematics is a book written by Bertrand Russell in 1903. In it he presented his famous paradox and argued his thesis that mathematics and logic are identical....
, Russell arrives at a discussion of Frege's notion of function, "...a point in which Frege's work is very important, and requires careful examination". In response to his 1902 exchange of letters with Frege about the contradiction he discovered in Frege's Begriffsschrift Russell tacked this section on at the last moment.
For Russell the bedeviling notion is that of "variable": "6. Mathematical propositions are not only characterized by the fact that they assert implications, but also by the fact that they contain variables. The notion of the variable is one of the most difficult with which logic has to deal. For the present, I openly wish to make it plain that there are variables in all mathematical propositions, even where at first sight they might seem to be absent. . . . We shall find always, in all mathematical propositions, that the words any or some occur; and these words are the marks of a variable and a formal implication".
As expressed by Russell "the process of transforming constants in a proposition into variables leads to what is called generalization, and gives us, as it were, the formal essence of a proposition ... So long as any term in our proposition can be turned into a variable, our proposition can be generalized; and so long as this is possible, it is the business of mathematics to do it"; these generalizations Russell named propositional functions". Indeed he cites and quotes from Frege's BegriffsschriftBegriffsschriftBegriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
and presents a vivid example from Frege's 1891 Function und Begriff: That "the essence of the arithmetical function 2x3 + x is what is left when the x is taken away, i.e., in the above instance 2( )3 + ( ). The argument x does not belong to the function but the two taken together make the whole". Russell agreed with Frege's notion of "function" in one sense: "He regards functions – and in this I agree with him – as more fundamental than predicates and relations" but Russell rejected Frege's "theory of subject and assertion", in particular "he thinks that, if a term a occurs in a proposition, the proposition can always be analysed into a and an assertion about a".
Evolution of Russell's notion of "function" 1908–1913
Russell would carry his ideas forward in his 1908 Mathematical logical as based on the theory of types and into his and Whitehead's 1910–1913 Principia Mathematica. By the time of Principia Mathematica Russell, like Frege, considered the propositional function fundamental: "Propositional functions are the fundamental kind from which the more usual kinds of function, such as “sin ‘’x’’ or log x or "the father of x" are derived. These derivative functions . . . are called “descriptive functions". The functions of propositions . . . are a particular case of propositional functions".
Propositional functionPropositional functionA propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
s: Because his terminology is different from the contemporary, the reader may be confused by Russell's "propositional function". An example may help. Russell writes a propositional function in its raw form, e.g., as φŷ: "ŷ is hurt". (Observe the circumflex or "hat" over the variable y). For our example, we will assign just 4 values to the variable ŷ: "Bob", "This bird", "Emily the rabbit", and "y". Substitution of one of these values for variable ŷ yields a proposition; this proposition is called a "value" of the propositional function. In our example there are four values of the propositional function, e.g., "Bob is hurt", "This bird is hurt", "Emily the rabbit is hurt" and "y is hurt." A proposition, if it is significant—i.e., if its truth is determinate—has a truth-value of truth or falsity. If a proposition's truth value is "truth" then the variable's value is said to satisfy the propositional function. Finally, per Russell's definition, "a class [set] is all objects satisfying some propositional function" (p. 23). Note the word "all'" – this is how the contemporary notions of "For all ∀" and "there exists at least one instance ∃" enter the treatment (p. 15).
To continue the example: Suppose (from outside the mathematics/logic) one determines that the propositions "Bob is hurt" has a truth value of "falsity", "This bird is hurt" has a truth value of "truth", "Emily the rabbit is hurt" has an indeterminate truth value because "Emily the rabbit" doesn't exist, and "y is hurt" is ambiguous as to its truth value because the argument y itself is ambiguous. While the two propositions "Bob is hurt" and "This bird is hurt" are significant (both have truth values), only the value "This bird" of the variable ŷ satisfies the propositional function φŷ: "ŷ is hurt". When one goes to form the class α: φŷ: "ŷ is hurt", only "This bird" is included, given the four values "Bob", "This bird", "Emily the rabbit" and "y" for variable ŷ and their respective truth-values: falsity, truth, indeterminate, ambiguous.
Russell defines functions of propositions with arguments, and truth-functions f(p). For example, suppose one were to form the "function of propositions with arguments" p1: "NOT(p) AND q" and assign its variables the values of p: "Bob is hurt" and q: "This bird is hurt". (We are restricted to the logical linkages NOT, AND, OR and IMPLIES, and we can only assign "significant" propositions to the variables p and q). Then the "function of propositions with arguments" is p1: NOT("Bob is hurt") AND "This bird is hurt". To determine the truth value of this "function of propositions with arguments" we submit it to a "truth function", e.g., f(p1): f( NOT("Bob is hurt") AND "This bird is hurt" ), which yields a truth value of "truth".
The notion of a "many-one" functional relation": Russell first discusses the notion of "identity", then defines a descriptive function (pages 30ff) as the unique value ιx that satisfies the (2-variable) propositional function (i.e., "relation") φŷ.- N.B. The reader should be warned here that the order of the variables are reversed! y is the independent variable and x is the dependent variable, e.g., x = sin(y).
Russell symbolizes the descriptive function as "the object standing in relation to y": R'y =DEF (ιx)(x R y). Russell repeats that "R'y is a function of y, but not a propositional function [sic]; we shall call it a descriptive function. All the ordinary functions of mathematics are of this kind. Thus in our notation "sin y" would be written " sin 'y ", and "sin" would stand for the relation sin 'y has to y".
Hardy 1908
defined a function as a relation between two variables x and y such that "to some values of x at any rate correspond values of y." He neither required the function to be defined for all values of x nor to associate each value of x to a single value of y. This broad definition of a function encompasses more relations than are ordinarily considered functions in contemporary mathematics.
The Formalist's "function": David Hilbert's axiomatization of mathematics (1904–1927)
David HilbertDavid HilbertDavid Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
set himself the goal of "formalizing" classical mathematics "as a formal axiomatic theory, and this theory shall be proved to be consistent, i.e., free from contradiction" . In his 1927 The Foundations of Mathematics Hilbert frames the notion of function in terms of the existence of an "object":- 13. A(a) --> A(ε(A)) Here ε(A) stands for an object of which the proposition A(a) certainly holds if it holds of any object at all; let us call ε the logical ε-function". [The arrow indicates “implies”.]
Hilbert then illustrates the three ways how the ε-function is to be used, firstly as the "for all" and "there exists" notions, secondly to represent the "object of which [a proposition] holds", and lastly how to cast it into the choice function.
Recursion theory and computability: But the unexpected outcome of Hilbert's and his student BernaysBernaysBernays is a surname and may refer to:* Isaac Bernays , a German rabbi, and father of:** Jakob Bernays , a German classical linguist** Michael Bernays , a German literature historian...
's effort was failure; see Gödel's incompleteness theoremsGödel's incompleteness theoremsGödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
of 1931. At about the same time, in an effort to solve Hilbert's EntscheidungsproblemEntscheidungsproblemIn mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...
, mathematicians set about to define what was meant by an "effectively calculable function" (Alonzo ChurchAlonzo ChurchAlonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
1936), i.e., "effective method" or "algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
", that is, an explicit, step-by-step procedure that would succeed in computing a function. Various models for algorithms appeared, in rapid succession, including Church's lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
(1936), Stephen Kleene's μ-recursive functionsMu-recursive functionIn mathematical logic and computer science, the μ-recursive functions are a class of partial functions from natural numbers to natural numbers which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that...
(1936) and Alan TuringAlan TuringAlan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
's (1936–7) notion of replacing human "computers" with utterly-mechanical "computing machines" (see Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s). It was shown that all of these models could compute the same class of computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s. Church's thesis holds that this class of functions exhausts all the number-theoretic functions that can be calculated by an algorithm. The outcomes of these efforts were vivid demonstrations that, in Turing's words, "there can be no general process for determining whether a given formula U of the functional calculus K [Principia Mathematica] is provable"; see more at Independence (mathematical logic)Independence (mathematical logic)In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...
and Computability theoryComputability theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
.
Development of the set-theoretic definition of "function"
Set theory began with the work of the logicians with the notion of "class" (modern "set") for example De MorganAugustus De MorganAugustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....
(1847), JevonsWilliam Stanley JevonsWilliam Stanley Jevons was a British economist and logician.Irving Fisher described his book The Theory of Political Economy as beginning the mathematical method in economics. It made the case that economics as a science concerned with quantities is necessarily mathematical...
(1880), VennJohn VennDonald A. Venn FRS , was a British logician and philosopher. He is famous for introducing the Venn diagram, which is used in many fields, including set theory, probability, logic, statistics, and computer science....
1881, Frege 1879 and Peano (1889). It was given a push by Georg CantorGeorg CantorGeorg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
's attempt to define the infinite in set-theoretic treatment (1870–1890) and a subsequent discovery of an antinomyAntinomyAntinomy literally means the mutual incompatibility, real or apparent, of two laws. It is a term used in logic and epistemology....
(contradiction, paradox) in this treatment (Cantor's paradoxCantor's paradoxIn set theory, Cantor's paradox is derivable from the theorem that there is no greatest cardinal number, so that the collection of "infinite sizes" is itself infinite...
), by Russell's discovery (1902) of an antinomy in Frege's 1879 (Russell's paradoxRussell's paradoxIn the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
), by the discovery of more antinomies in the early 20th century (e.g., the 1897 Burali-Forti paradoxBurali-Forti paradoxIn set theory, a field of mathematics, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal numbers" leads to a contradiction and therefore shows an antinomy in a system that allows its construction...
and the 1905 Richard paradox), and by resistance to Russell's complex treatment of logic and dislike of his axiom of reducibilityAxiom of reducibilityThe axiom of reducibility was introduced by Bertrand Russell as part of his ramified theory of types, an attempt to ground mathematics in first-order logic.- History: the problem of impredicativity :...
(1908, 1910–1913) that he proposed as a means to evade the antinomies.
Russell's paradox 1902
In 1902 Russell sent a letter to Frege pointing out that Frege's 1879 Begriffsschrift allowed a function to be an argument of itself: "On the other hand, it may also be that the argument is determinate and the function indeterminate . . .." From this unconstrained situation Russell was able to form a paradox:- "You state ... that a function, too, can act as the indeterminate element. This I formerly believed, but now this view seems doubtful to me because of the following contradiction. Let w be the predicate: to be a predicate that cannot be predicated of itself. Can w be predicated of itself?"
Frege responded promptly that "Your discovery of the contradiction caused me the greatest surprise and, I would almost say, consternation, since it has shaken the basis on which I intended to build arithmetic".
From this point forward development of the foundations of mathematics became an exercise in how to dodge "Russell's paradox", framed as it was in "the bare [set-theoretic] notions of set and element".
Zermelo's set theory (1908) modified by Skolem (1922)
The notion of "function" appears as Zermelo's axiom III—the Axiom of Separation (Axiom der Aussonderung). This axiom constrains us to use a propositional function Φ(x) to "separate" a subset MΦ from a previously formed set M:- "AXIOM III. (Axiom of separation). Whenever the propositional function Φ(x) is definite for all elements of a set M, M possesses a subset MΦ containing as elements precisely those elements x of M for which Φ(x) is true".
As there is no universal set—sets originate by way of Axiom II from elements of (non-set) domain B – "...this disposes of the Russell antinomy so far as we are concerned". But Zermelo's "definite criterion" is imprecise, and is fixed by Weyl, Fraenkel, Skolem, and von Neumann.
In fact Skolem in his 1922 referred to this "definite criterion" or "property" as a "definite proposition":- "... a finite expression constructed from elementary propositions of the form a ε b or a = b by means of the five operations [logical conjunction, disjunction, negation, universal quantification, and existential quantification].
van HeijenoortJean Van HeijenoortJean Louis Maxime van Heijenoort was a pioneer historian of mathematical logic. He was also a personal secretary to Leon Trotsky from 1932 to 1939, and from then until 1947, an American Trotskyist activist.-Life:Van Heijenoort was born in Creil, France...
summarizes:- "A property is definite in Skolem's sense if it is expressed . . . by a well-formed formula in the simple predicate calculus of first order in which the sole predicate constants are ε and possibly, =. ... Today an axiomatization of set theory is usually embedded in a logical calculus, and it is Weyl'sHermann WeylHermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
and Skolem's approach to the formulation of the axiom of separation that is generally adopted.
In this quote the reader may observe a shift in terminology: nowhere is mentioned the notion of "propositional function", but rather one sees the words "formula", "predicate calculus", "predicate", and "logical calculus." This shift in terminology is discussed more in the section that covers "function" in contemporary set theory.
The Wiener–Hausdorff–Kuratowski "ordered pair" definition 1914–1921
The history of the notion of "ordered pair" is not clear. As noted above, Frege (1879) proposed an intuitive ordering in his definition of a two-argument function Ψ(A, B). Norbert WienerNorbert WienerNorbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
in his 1914 (see below) observes that his own treatment essentially "revert(s) to Schröder'sErnst SchröderErnst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
treatment of a relation as a class of ordered couples". Russell (1903) considered the definition of a relation (such as Ψ(A, B)) as a "class of couples" but rejected it:- "There is a temptation to regard a relation as definable in extension as a class of couples. This is the formal advantage that it avoids the necessity for the primitive proposition asserting that every couple has a relation holding between no other pairs of terms. But it is necessary to give sense to the couple, to distinguish the referent [domain] from the relatum [converse domain]: thus a couple becomes essentially distinct from a class of two terms, and must itself be introduced as a primitive idea. . . . It seems therefore more correct to take an intensional view of relations, and to identify them rather with class-concepts than with classes."
By 1910–1913 and Principia Mathematica Russell had given up on the requirement for an intensionalIntensional statementIn logic, an intensional statement-form is a statement-form with at least one instance such that substituting co-extensive expressions into it does not always preserve logical value. An intensional statement is a statement that is an instance of an intensional statement-form. Here co-extensive...
definition of a relation, stating that "mathematics is always concerned with extensions rather than intensions" and "Relations, like classes, are to be taken in extension". To demonstrate the notion of a relation in extensionExtension (predicate logic)The extension of a predicatea truth-valued functionis the set of tuples of values that, used as arguments, satisfy the predicate. Such a set of tuples is a relation.For example the statement "d2 is the weekday following d1"...
Russell now embraced the notion of ordered couple: "We may regard a relation ... as a class of couples ... the relation determined by φ(x, y) is the class of couples (x, y) for which φ(x, y) is true". In a footnote he clarified his notion and arrived at this definition:- "Such a couple has a sense, i.e., the couple (x, y) is different from the couple (y, x) unless x = y. We shall call it a "couple with sense," ... it may also be called an ordered couple.
But he goes on to say that he would not introduce the ordered couples further into his "symbolic treatment"; he proposes his "matrix" and his unpopular axiom of reducibility in their place.
An attempt to solve the problem of the antinomies led Russell to propose his "doctrine of types" in an appendix B of his 1903 The Principles of Mathematics. In a few years he would refine this notion and propose in his 1908 The Theory of Types two axioms of reducibilityAxiom of reducibilityThe axiom of reducibility was introduced by Bertrand Russell as part of his ramified theory of types, an attempt to ground mathematics in first-order logic.- History: the problem of impredicativity :...
, the purpose of which were to reduce (single-variable) propositional functions and (dual-variable) relations to a "lower" form (and ultimately into a completely extensionalExtensionalIn philosophy of language, a context in which a sub-sentential expression e appears is called extensional if and only if e can be replaced by an expression with the same extension and necessarily preserve truth-value. The extension of a term is the set of objects that that term denotes.Take the...
form); he and Alfred North WhiteheadAlfred North WhiteheadAlfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
would carry this treatment over to Principia Mathematica 1910–1913 with a further refinement called "a matrix". The first axiom is *12.1; the second is *12.11. To quote Wiener the second axiom *12.11 "is involved only in the theory of relations". Both axioms, however, were met with skepticism and resistance; see more at Axiom of reducibilityAxiom of reducibilityThe axiom of reducibility was introduced by Bertrand Russell as part of his ramified theory of types, an attempt to ground mathematics in first-order logic.- History: the problem of impredicativity :...
. By 1914 Norbert Wiener, using Whitehead and Russell's symbolism, eliminated axiom *12.11 (the "two-variable" (relational) version of the axiom of reducibility) by expressing a relation as an ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
"using the null set. At approximately the same time, HausdorffFelix HausdorffFelix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
(1914, p. 32) gave the definition of the ordered pair (a, b) as { {a,1}, {b, 2} }. A few years later Kuratowski (1921) offered a definition that has been widely used ever since, namely { {a, b}, {a} }". As noted by Suppes (1960) "This definition . . . was historically important in reducing the theory of relations to the theory of sets.
Observe that while Wiener "reduced" the relational *12.11 form of the axiom of reducibility he did not reduce nor otherwise change the propositional-function form *12.1; indeed he declared this "essential to the treatment of identity, descriptions, classes and relations".
Schönfinkel's notion of "function" as a many-one "correspondence" 1924
Where exactly the general notion of "function" as a many-one relationship derives from is unclear. Russell in his 1920 Introduction to Mathematical Philosophy states that "It should be observed that all mathematical functions result form one-many [sic – contemporary usage is many-one] relations . . . Functions in this sense are descriptive functions". A reasonable possibility is the Principia Mathematica notion of "descriptive function" – R 'y =DEF (ιx)(x R y): "the singular object that has a relation R to y". Whatever the case, by 1924, Moses SchonfinkelMoses SchönfinkelMoses Ilyich Schönfinkel, also known as Moisei Isai'evich Sheinfinkel , was a Russian logician and mathematician, known for the invention of combinatory logic.- Life :Schönfinkel attended the Novorossiysk University of Odessa, studying mathematics under Samuil Osipovich...
expressed the notion, claiming it to be "well known":- "As is well known, by function we mean in the simplest case a correspondence between the elements of some domain of quantities, the argument domain, and those of a domain of function values ... such that to each argument value there corresponds at most one function value".
According to Willard Quine, Schönfinkel's 1924 "provide[s] for ... the whole sweep of abstract set theory. The crux of the matter is that Schönfinkel lets functions stand as arguments. ¶ For Schönfinkel, substantially as for Frege, classes are special sorts of functions. They are propositional functions, functions whose values are truth values. All functions, propositional and otherwise, are for Schönfinkel one-place functions". Remarkably, Schönfinkel reduces all mathematics to an extremely compact functional calculus consisting of only three functions: Constancy, fusion (i.e., composition), and mutual exclusivity. Quine notes that Haskell CurryHaskell CurryHaskell Brooks Curry was an American mathematician and logician. Curry is best known for his work in combinatory logic; while the initial concept of combinatory logic was based on a single paper by Moses Schönfinkel, much of the development was done by Curry. Curry is also known for Curry's...
(1958) carried this work forward "under the head of combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
".
Von Neumann's set theory 1925
By 1925 Abraham Fraenkel (1922) and Thoralf SkolemThoralf SkolemThoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
(1922) had amended Zermelo's set theory of 1908. But von Neumann was not convinced that this axiomatization could not lead to the antinomies. So he proposed his own theory, his 1925 An axiomatization of set theory. It explicitly contains a "contemporary", set-theoretic version of the notion of "function":- "[Unlike Zermelo's set theory] [w]e prefer, however, to axiomatize not "set" but "function". The latter notion certainly includes the former. (More precisely, the two notions are completely equivalent, since a function can be regarded as a set of pairs, and a set as a function that can take two values.)".
His axiomatization creates two "domains of objects" called "arguments" (I-objects) and "functions" (II-objects); where they overlap are the "argument functions" (I-II objects). He introduces two "universal two-variable operations" – (i) the operation [x, y]: ". . . read 'the value of the function x for the argument y) and (ii) the operation (x, y): ". . . (read 'the ordered pair x, y'") whose variables x and y must both be arguments and that itself produces an argument (x,y)". To clarify the function pair he notes that "Instead of f(x) we write [f,x] to indicate that f, just like x, is to be regarded as a variable in this procedure". And to avoid the "antinomies of naive set theory, in Russell's first of all . . . we must forgo treating certain functions as arguments". He adopts a notion from Zermelo to restrict these "certain functions"
Notion of "function" in contemporary set theory
Both axiomatic and naive forms of Zermelo's set theory as modified by Fraenkel (1922) and Skolem (1922) define "function" as a relation, define a relation as a set of ordered pairs, and define an ordered pair as a set of two "dissymetric" sets.
While the reader of Suppes (1960) Axiomatic Set Theory or Halmos (1970) Naive Set Theory observes the use of function-symbolism in the axiom of separation, e.g., φ(x) (in Suppes) and S(x) (in Halmos), they will see no mention of "proposition" or even "first order predicate calculus". In their place are "expressions of the object language", "atomic formulae", "primitive formulae", and "atomic sentences".
Kleene 1952 defines the words as follows: "In word languages, a proposition is expressed by a sentence. Then a 'predicate' is expressed by an incomplete sentence or sentence skeleton containing an open place. For example, "___ is a man" expresses a predicate ... The predicate is a propositional function of one variable. Predicates are often called 'properties' ... The predicate calculus will treat of the logic of predicates in this general sense of 'predicate', i.e., as propositional function".
The reason for the disappearance of the words "propositional function" e.g., in Suppes (1960), and Halmos (1970), is explained by Alfred TarskiAlfred TarskiAlfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
1946 together with further explanation of the terminology:- "An expression such as x is an integer, which contains variables and, on replacement of these variables by constants becomes a sentence, is called a SENTENTIAL [i.e., propositional cf his index] FUNCTION. But mathematicians, by the way, are not very fond of this expression, because they use the term "function" with a different meaning. ... sentential functions and sentences composed entirely of mathematical symbols (and not words of everyday languange), such as: x + y = 5 are usually referred to by mathematicians as FORMULAE. In place of "sentential function" we shall sometimes simply say "sentence" – but only in cases where there is no danger of any misunderstanding".
For his part Tarski calls the relational form of function a "FUNCTIONAL RELATION or simply a FUNCTION" . After a discussion of this "functional relation" he asserts that:- "The concept of a function which we are considering now differs essentially from the concepts of a sentential [propositional] and of a designatory function .... Strictly speaking ... [these] do not belong to the domain of logic or mathematics; they denote certain categories of expressions which serve to compose logical and mathematical statements, but they do not denote things treated of in those statements... . The term "function" in its new sense, on the other hand, is an expression of a purely logical character; it designates a certain type of things dealt with in logic and mathematics."
See more about "truth under an interpretation" at Alfred Tarski.
Further developments
The idea of structureMathematical structureIn mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
-preserving functions, or homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s, led to the abstract notion of morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
, the key concept of category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. More recently, the concept of functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
has been used as an analogue of a function in category theory.
See also
- FunctionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
- Function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
- Functional decompositionFunctional decompositionFunctional decomposition refers broadly to the process of resolving a functional relationship into its constituent parts in such a way that the original function can be reconstructed from those parts by function composition...
- Functional predicateFunctional predicateIn formal logic and related branches of mathematics, a functional predicate, or function symbol, is a logical symbol that may be applied to an object term to produce another object term....
- Functional programmingFunctional programmingIn computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
- FunctorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
- Generalized functionGeneralized functionIn mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
- Implicit functionImplicit functionThe implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
- List of mathematical functions
- Parametric equationParametric equationIn mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
- PlateauPlateau (mathematics)A plateau of a function is a part of its domain where the function has constant value.More formally, let U, V be topological spaces. A plateau for a function f: U → V is a path-connected set of points P of U such that for some y we havefor all p in P....
- ProportionalityProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
- Vertical line testVertical line testIn mathematics, the vertical line test is a test to determine if a curve is a relation or graph of a function when the function's domain and Range correspond to the x and y axes of the Cartesian coordinate system...
External links
- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- Shodor: Function Flyer, interactive Java applet for graphing and exploring functions.
- xFunctions, a Java applet for exploring functions graphically.
- Draw Function Graphs, online drawing program for mathematical functions.
- Functions from cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
. - Function at ProvenMath.
- Comprehensive web-based function graphing & evaluation tool.
- FunctionGame, an educational interactive function guessing game.