Burali-Forti paradox
Encyclopedia
In set theory
, a field of mathematics
, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal number
s" leads to a contradiction and therefore shows an antinomy
in a system that allows its construction. It is named after Cesare Burali-Forti
, who discovered it in 1897.
carries all properties of an ordinal number and would have to be considered an ordinal number itself. Then, we can construct its successor 
, which is strictly greater than 
. However, this ordinal number must be an element of 
since 
contains all ordinal numbers, and we arrive at
, under which each ordinal is the set of all preceding ordinals, which was not known at the time the paradox was framed by Burali-Forti.
Here is an account with fewer presuppositions: suppose that we associate with each well-ordering
an object called its "order type
" in an unspecified way (the order types are the ordinal numbers). The "order types" (ordinal numbers) themselves are well-ordered in a natural way,
and this well-ordering must have an order type
. It is easily shown in
naïve set theory
(and remains true in ZFC but not in New Foundations
) that the order
type of all ordinal numbers less than a fixed
is 
itself.
So the order
type of all ordinal numbers less than
is 
itself. But
this means that
, being the order type of a proper initial segment of the ordinals, is strictly less than the order type of all the ordinals,
but the latter is
itself by definition. This is a contradiction.
If we use the von Neumann definition, under which each ordinal is identified as the set of all preceding ordinals, the paradox is unavoidable: the offending proposition that the order type of all ordinal numbers less than a fixed
is 
itself must be true. The collection of von Neumann ordinals, like the collection in the Russell paradox, cannot be a set in any set theory with classical logic. But the collection of order types in New Foundations (defined as equivalence classes of well-orderings under similarity) is actually a set, and the paradox is avoided because the order type of the ordinals less than 
turns out not to be
.
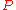", as it was for example possible in Gottlob Frege
's axiom system. New Foundations
uses a different solution.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a field of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s" leads to a contradiction and therefore shows an antinomy
Antinomy
Antinomy literally means the mutual incompatibility, real or apparent, of two laws. It is a term used in logic and epistemology....
in a system that allows its construction. It is named after Cesare Burali-Forti
Cesare Burali-Forti
Cesare Burali-Forti was an Italian mathematician.He was born in Arezzo, and was an assistant of Giuseppe Peano in Turin from 1894 to 1896, during which time he discovered what came to be called the Burali-Forti paradox of Cantorian set theory. He died in Turin.-Books by C. Burali-Forti:* with R....
, who discovered it in 1897.
Stated in terms of von Neumann ordinals
The reason is that the set of all ordinal numbers carries all properties of an ordinal number and would have to be considered an ordinal number itself. Then, we can construct its successor , which is strictly greater than . However, this ordinal number must be an element of since contains all ordinal numbers, and we arrive atStated more generally
The version of the paradox above is anachronistic, because it presupposes the definition of the ordinals due to John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, under which each ordinal is the set of all preceding ordinals, which was not known at the time the paradox was framed by Burali-Forti.
Here is an account with fewer presuppositions: suppose that we associate with each well-ordering
an object called its "order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
" in an unspecified way (the order types are the ordinal numbers). The "order types" (ordinal numbers) themselves are well-ordered in a natural way,
and this well-ordering must have an order type
. It is easily shown innaïve set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
(and remains true in ZFC but not in New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
) that the order
type of all ordinal numbers less than a fixed
is itself.So the order
type of all ordinal numbers less than
is itself. Butthis means that
, being the order type of a proper initial segment of the ordinals, is strictly less than the order type of all the ordinals,but the latter is
itself by definition. This is a contradiction.If we use the von Neumann definition, under which each ordinal is identified as the set of all preceding ordinals, the paradox is unavoidable: the offending proposition that the order type of all ordinal numbers less than a fixed
is itself must be true. The collection of von Neumann ordinals, like the collection in the Russell paradox, cannot be a set in any set theory with classical logic. But the collection of order types in New Foundations (defined as equivalence classes of well-orderings under similarity) is actually a set, and the paradox is avoided because the order type of the ordinals less than turns out not to be
.Resolution of the paradox
Modern axiomatic set theory such as ZF and ZFC circumvents this antinomy by simply not allowing construction of sets with unrestricted comprehension terms like "all sets with the property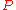", as it was for example possible in Gottlob FregeGottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
's axiom system. New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
uses a different solution.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: "Paradoxes and Contemporary Logic" -- by Andrea Cantini.