
Surjective function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
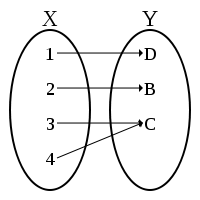
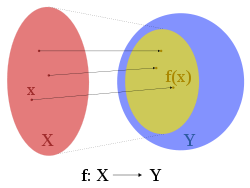
, a function f from a set X to a set Y is surjective (or onto), or a surjection, if every element y in Y has a corresponding element x in X so that f(x) = y. Multiple elements of X might be turned into the same element of Y by applying f.
The term surjective and the related terms injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and bijective were introduced by Nicolas Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
, a group of mainly French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
20th-century mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s who wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. The French prefix
Prefix
A prefix is an affix which is placed before the root of a word. Particularly in the study of languages,a prefix is also called a preformative, because it alters the form of the words to which it is affixed.Examples of prefixes:...
sur means over or above and relates to the fact that the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the domain of a surjective function completely covers the function's codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
.
Definition
A surjective function is a function whose image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
is equal to its codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
. Equivalently, a function f with domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
X and codomain Y is surjective if for every y in Y there exists at least one x in X with
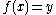 . Surjections are sometimes denoted by a two-headed rightwards arrow, as in f : X ↠ Y.
. Surjections are sometimes denoted by a two-headed rightwards arrow, as in f : X ↠ Y.Examples
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
idX on X is surjective.
The function defined by f(n) = n mod
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
2 and mapping even integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s to 0 and odd integers to 1 is surjective.
The function defined by f(x) = 2x + 1 is surjective (and even bijective), because for every real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
y we have an x such that f(x) = y: an appropriate x is (y − 1)/2.
The function defined by g(x) = x2 is not surjective, because there is no real number x such that x2 = −1. However, the function defined by g(x) = x2 (with restricted codomain) is surjective because for every y in the positive real codomain Y there is at least one x in the real domain X such that |x2 = y.
The natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
function is a surjective and even bijective mapping from the set of positive real numbers to the set of all real numbers. Its inverse, the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, is not surjective as its range is the set of positive real numbers and its domain is usually defined to be the set of all real numbers. The matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
is not surjective when seen as a map from the space of all n×n matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
to itself. It is, however, usually defined as a map from the space of all n×n matrices to the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of degree n, i.e. the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all n×n invertible matrices. Under this definition the matrix exponential is surjective for complex matrices, although still not surjective for real matrices.
The projection from a cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
to one of its factors is surjective.
In a 3D video game vectors are projected onto a 2D flat screen by means of a surjective function.
Properties
A function is bijective if and only if it is both surjective and injectiveInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
.
If (as is often done) a function is identified with its graph, then surjectivity is not a property of the function itself, but rather a relationship between the function and its codomain. Unlike injectivity, surjectivity cannot be read off of the graph of the function alone.
Surjections as right invertible functions
The function is said to be a right inverse of the function if f(g(y)) = y for every y in Y (g can be undone by f). In other words, g is a right inverse of f if the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of g and f in that order is the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on the domain Y of g. The function g need not be a complete inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of f because the composition in the other order, , may not be the identity function on the domain X of f. In other words, f can undo or "reverse" g, but cannot necessarily be reversed by it.
Every function with a right inverse is necessarily a surjection. The proposition that every surjective function has a right inverse is equivalent to the axiom of choice.
If is surjective and B is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Y, then f(f −1(B)) = B. Thus, B can be recovered from its preimage .
For example, in the first illustration, there is some function g such that g(C) = 4. There is also some function f such that f(4) = C. It doesn't matter that g(C) can also equal 3; it only matters that f "reverses" g.
Surjections as epimorphisms
A function is surjective if and only if it is right-cancellative: given any functions , whenever g o f = h o f, then g = h. This property is formulated in terms of functions and their compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and can be generalized to the more general notion of the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s of a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and their composition. Right-cancellative morphisms are called epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s. Specifically, surjective functions are precisely the epimorphisms in the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. The prefix epi is derived from the greek preposition ἐπί meaning over, above, on.
Any morphism with a right inverse is an epimorphism, but the converse is not true in general. A right inverse g of a morphism f is called a section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of f. A morphism with a right inverse is called a split epimorphism.
Surjections as binary relations
Any function with domain X and codomain Y can be seen as a left-total and right-unique binary relation between X and Y by identifying it with its function graph. A surjective function with domain X and codomain Y is then a binary relation between X and Y that is right-unique and both left-total and right-total.Cardinality of the domain of a surjection
The cardinality of the domain of a surjective function is greater than or equal to the cardinality of its codomain: If is a surjective function, then X has at least as many elements as Y, in the sense of cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s. (The proof appeals to the axiom of choice to show that a function
satisfying f(g(y))=y for all y in Y exists. g is easily seen to be injective, thus the formal definition of |Y|≤|X| is satisfied.)
Specifically, if both X and Y are finite with the same number of elements, then is surjective if and only if f is injective.
Composition and decomposition
The compositeFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of surjective functions is always surjective: If f and g are both surjective, and the codomain of g is equal to the domain of f, then is surjective. Conversely, if is surjective, then f is surjective (but g, the function applied first, need not be). These properties generalize from surjections in the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
to any epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s in any category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
Any function can be decomposed into a surjection and an injection
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
: For any function there exist a surjection and an injection such that h = g o f. To see this, define Y to be the sets where z is in Z. These sets are disjoint and partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
X. Then f carries each x to the element of Y which contains it, and g carries each element of Y to the point in Z to which h sends its points. Then f is surjective since it is a projection map, and g is injective by definition.
Induced surjection and induced bijection
Any function induces a surjection by restricting its codomain to its range. Any surjective function induces a bijection defined on a quotient of its domain by collapsing all arguments mapping to a given fixed image. More precisely, every surjection can be factored as a projection followed by a bijection as follows. Let A/~ be the equivalence classes of A under the following equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
: x ~ y if and only if f(x) = f(y). Equivalently, A/~ is the set of all preimages under f. Let P(~) : A → A/~ be the projection map which sends each x in A to its equivalence class [x]~, and let fP : A/~ → B be the well-defined function given by fP([x]~) = f(x). Then f = fP o P(~).
See also
- Cover (algebra)Cover (algebra)In abstract algebra, a cover is one instance of some mathematical structure mapping onto another instance, such as a group covering a subgroup. This should not be confused with the concept of a cover in topology....
- Covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
- EnumerationEnumerationIn mathematics and theoretical computer science, the broadest and most abstract definition of an enumeration of a set is an exact listing of all of its elements . The restrictions imposed on the type of list used depend on the branch of mathematics and the context in which one is working...
- Fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
- Index setIndex setIn mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
- Section (category theory)Section (category theory)In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...

