.gif)
Proportionality (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, two variable quantities
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
are proportional if one of them is always the product of the other and a constant quantity, called the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
of proportionality or proportionality constant. In other words, are proportional if the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
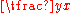 is constant. We also say that one of the quantities is proportional to the other. For example, if the speed of an object is constant, it travels a distance that is proportional to the travel time.
is constant. We also say that one of the quantities is proportional to the other. For example, if the speed of an object is constant, it travels a distance that is proportional to the travel time.If a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
transforms into and if the product is not zero, we say are proportional An equality of two ratios such as
 where no term is zero, is called a proportion.
where no term is zero, is called a proportion.
Geometric illustration
When the duplication of a given rectangle preserves its shape, the ratio of the large dimension to the small dimension is a constant number in all the copies, and in the original rectangle. The largest rectangle of the drawing is similarSimilarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to one or the other rectangle with stripes. From their width to their height, the coefficient is
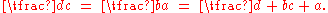 A ratio of their dimensions horizontally written within the image, at the top or the bottom, determines the common shape of the three similar rectangles.
A ratio of their dimensions horizontally written within the image, at the top or the bottom, determines the common shape of the three similar rectangles.The common diagonal of the similar rectangles divides each rectangle into two superposable triangles, with two different kinds of stripes. The four striped triangles and the two striped rectangles have a common vertex: the center of an homothetic transformation with a negative ratio – k or
 , that transforms one triangle and its stripes into another triangle with the same stripes, enlarged or reduced. The duplication scale of a striped triangle is the proportionality constant between the corresponding sides lengths of the triangles, equal to a positive ratio obliquely written within the image:
, that transforms one triangle and its stripes into another triangle with the same stripes, enlarged or reduced. The duplication scale of a striped triangle is the proportionality constant between the corresponding sides lengths of the triangles, equal to a positive ratio obliquely written within the image: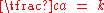 or
or 
In the proportion
 , the terms a and d are called the extremes, while b and c are the means, because a and d are the extreme terms of the list while b and c are in the middle of the list. From any proportion, we get another proportion by inverting the extremes or the means. And the product of the extremes equals the product of the means. Within the image, a double arrow indicates two inverted terms of the first proportion.
, the terms a and d are called the extremes, while b and c are the means, because a and d are the extreme terms of the list while b and c are in the middle of the list. From any proportion, we get another proportion by inverting the extremes or the means. And the product of the extremes equals the product of the means. Within the image, a double arrow indicates two inverted terms of the first proportion.Consider dividing the largest rectangle in two triangles, cutting along the diagonal. If we remove two triangles from either half rectangle, we get one of the plain gray rectangles. Above and below this diagonal, the areas
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the two biggest triangles of the drawing are equal, because these triangles are superposable. Above and below the subtracted areas are equal for the same reason. Therefore, the two plain gray rectangles have the same area:
Symbol
The mathematical symbol '∝' is used to indicate that two values are proportional. For example, A ∝ B.In Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
this is symbol U+221D
Unicode Mathematical Operators
Unicode ranges mathematical operators and symbols in multiple blocks.* Mathematical Operators * Miscellaneous Mathematical Symbols-A * Miscellaneous Mathematical Symbols-B...
.
Direct proportionality
Given two variables x and y, y is (directly) proportional to x (x and y vary directly, or x and y are in direct variation) if there is a non-zero constant k such that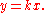
The relation is often denoted

and the constant ratio
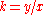
is called the proportionality constant or constant of proportionality.
Examples
- If an object travels at a constant speedSpeedIn kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
, then the distanceDistanceDistance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
traveled is proportional to the timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
spent traveling, with the speed being the constant of proportionality.
- The circumferenceCircumferenceThe circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is proportional to its diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
, with the constant of proportionality equal to πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
- On a mapMapA map is a visual representation of an area—a symbolic depiction highlighting relationships between elements of that space such as objects, regions, and themes....
drawn to scaleScale (map)The scale of a map is defined as the ratio of a distance on the map to the corresponding distance on the ground.If the region of the map is small enough for the curvature of the Earth to be neglected, then the scale may be taken as a constant ratio over the whole map....
, the distance between any two points on the map is proportional to the distance between the two locations that the points represent, with the constant of proportionality being the scale of the map.
- The force acting on a certain object due to gravity is proportional to the object's massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
; the constant of proportionality between the mass and the force is known as gravitational accelerationGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
.
Properties
Since
is equivalent to
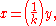
it follows that if y is proportional to x, with (nonzero) proportionality constant k, then x is also proportional to y with proportionality constant 1/k.
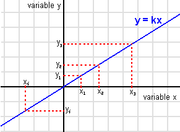
If y is proportional to x, then the graph of y as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of x will be a straight line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
passing through the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
with the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the line equal to the constant of proportionality: it corresponds to linear growth.
Inverse proportionality
The concept of inverse proportionality can be contrasted against direct proportionality. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constantCeteris paribus
or is a Latin phrase, literally translated as "with other things the same," or "all other things being equal or held constant." It is an example of an ablative absolute and is commonly rendered in English as "all other things being equal." A prediction, or a statement about causal or logical...
, the magnitude or absolute value of one inversely proportional variable will decrease if the other variable increases, while their product (the constant of proportionality k) is always the same.
Formally, two variables are inversely proportional (or varying inversely, or in inverse variation, or in inverse proportion or in reciprocal proportion) if one of the variables is directly proportional with the multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
(reciprocal) of the other, or equivalently if their product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
is a constant. It follows that the variable y is inversely proportional to the variable x if there exists a non-zero constant k such that
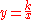
The constant can be found by multiplying the original x variable and the original y variable.
As an example, the time taken for a journey is inversely proportional to the speed of travel; the time needed to dig a hole is (approximately) inversely proportional to the number of people digging.
The graph of two variables varying inversely on the Cartesian coordinate plane is a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. The product of the X and Y values of each point on the curve will equal the constant of proportionality (k). Since neither x nor y can equal zero (if k is non-zero), the graph will never cross either axis.
Hyperbolic coordinates
The concepts of direct and inverse proportion lead to the location of points in the Cartesian plane by hyperbolic coordinates; the two coordinates correspond to the constant of direct proportionality that locates a point on a ray and the constant of inverse proportionality that locates a point on a hyperbola.Exponential and logarithmic proportionality
A variable y is exponentially proportional to a variable x, if y is directly proportional to the exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
of x, that is if there exist non-zero constants k and a
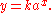
Likewise, a variable y is logarithmically proportional to a variable x, if y is directly proportional to the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of x, that is if there exist non-zero constants k and a
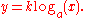
Experimental determination
To determine experimentally whether two physicalPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
quantities are directly proportional, one performs several measurements and plots the resulting data points in a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. If the points lie on or close to a straight line that passes through the origin (0, 0), then the two variables are probably proportional, with the proportionality constant given by the line's slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
.
See also
- CorrelationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
- Eudoxus of CnidusEudoxus of CnidusEudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
- Golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
- Proportional font
- Rule of three (mathematics)
- Sample sizeSample sizeSample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
- SimilaritySimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
Growth
- Linear growth
- Hyperbolic growthHyperbolic growthWhen a quantity grows towards a singularity under a finite variation it is said to undergo hyperbolic growth.More precisely, the reciprocal function 1/x has a hyperbola as a graph, and has a singularity at 0, meaning that the limit as x \to 0 is infinity: any similar graph is said to exhibit...

