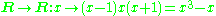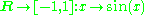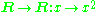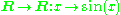Bijection, injection and surjection
Encyclopedia
In mathematics
, injections, surjections and bijections are classes of functions
distinguished by the manner in which arguments
(input expressions
from the domain
) and images
(output expressions from the codomain
) are related or mapped to each other.
A function maps elements from its domain to elements in its codomain.
An injective function is an injection.
A surjective function is a surjection.
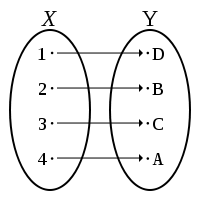
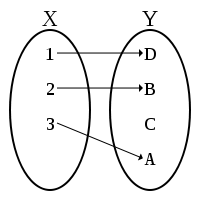
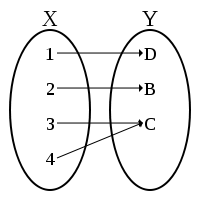
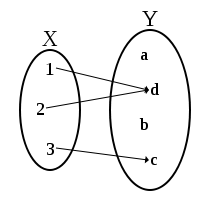
An injective function need not be surjective (not all elements of the codomain may be associated with arguments), and a surjective function need not be injective (some images may be associated with more than one argument). The four possible combinations of injective and surjective features are illustrated in the following diagrams.
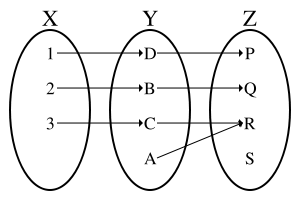 A function is injective (one-to-one) if every possible element of the codomain is mapped to by at most one argument. Equivalently, a function is injective if it maps distinct arguments to distinct images. An injective function is an injection. The formal definition is the following.
A function is injective (one-to-one) if every possible element of the codomain is mapped to by at most one argument. Equivalently, a function is injective if it maps distinct arguments to distinct images. An injective function is an injection. The formal definition is the following.
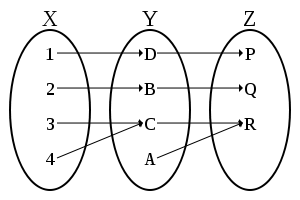 A function is surjective (onto) if every possible image is mapped to by at least one argument. In other words, every element in the codomain has non-empty preimage. Equivalently, a function is surjective if its image is equal to its codomain. A surjective function is a surjection. The formal definition is the following.
A function is surjective (onto) if every possible image is mapped to by at least one argument. In other words, every element in the codomain has non-empty preimage. Equivalently, a function is surjective if its image is equal to its codomain. A surjective function is a surjection. The formal definition is the following.
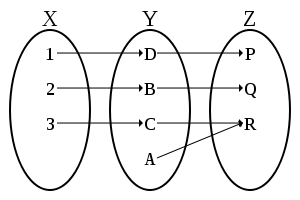 A function is bijective if it is both injective and surjective. A bijective function is a bijection (one-to-one correspondence). A function is bijective if and only if
A function is bijective if it is both injective and surjective. A bijective function is a bijection (one-to-one correspondence). A function is bijective if and only if
every possible image is mapped to by exactly one argument. This equivalent condition is formally expressed as follows.
Likewise, we can say that set "has fewer than or the same number of elements" as set
"has fewer than or the same number of elements" as set 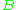 if there is an injection from
if there is an injection from 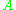 to
to 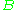 . We can also say that set
. We can also say that set 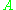 "has fewer than the number of elements" in set
"has fewer than the number of elements" in set 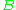 if there is an injection from
if there is an injection from 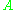 to
to 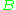 but not a bijection between
but not a bijection between 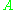 and
and 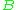 .
.
of sets, injections, surjections, and bijections correspond precisely to monomorphism
s, epimorphism
s, and isomorphism
s, respectively.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, injections, surjections and bijections are classes of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
distinguished by the manner in which arguments
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
(input expressions
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
from the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
) and images
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
(output expressions from the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
) are related or mapped to each other.
A function maps elements from its domain to elements in its codomain.
- A function
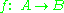 is injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
is injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
(one-to-one) if every element of the codomain is mapped to by at most one element of the domain. Notationally,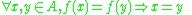 or, equivalently,
or, equivalently,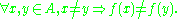
An injective function is an injection.
- A function is surjectiveSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
(onto) if every element of the codomain is mapped to by at least one element of the domain. (That is, the image and the codomain of the function are equal.) Notationally,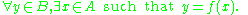
A surjective function is a surjection.
- A function is bijective (one-to-one and onto or one-to-one correspondence) if every element of the codomain is mapped to by exactly one element of the domain. (That is, the function is both injective and surjective.) A bijective function is a bijection.
An injective function need not be surjective (not all elements of the codomain may be associated with arguments), and a surjective function need not be injective (some images may be associated with more than one argument). The four possible combinations of injective and surjective features are illustrated in the following diagrams.
 |
 |
 |
 |
Injection

- The function
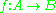 is injective iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
is injective iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
for all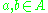 , we have
, we have 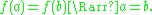
- A function f : A → B is injective if and only if A is empty or f is left-invertible; that is, there is a function g : f(A) → A such that g o f = identity function on A. Here f(A) is the image of f.
- Since every function is surjective when its codomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
is restricted to its imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
, every injection induces a bijection onto its image. More precisely, every injection f : A → B can be factored as a bijection followed by an inclusion as follows. Let fR : A → f(A) be f with codomain restricted to its image, and let i : f(A) → B be the inclusion map from f(A) into B. Then f = i o fR. A dual factorisation is given for surjections below. - The composition of two injections is again an injection, but if g o f is injective, then it can only be concluded that f is injective. See the figure at right.
- Every embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
is injective.
Surjection

- The function
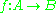 is surjective iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
is surjective iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
for all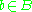 , there is
, there is 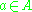 such that
such that 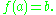
- A function f : A → B is surjective if and only if it is right-invertible, that is, if and only if there is a function g: B → A such that f o g = identity function on B. (This statement is equivalent to the axiom of choice.)
- By collapsing all arguments mapping to a given fixed image, every surjection induces a bijection defined on a quotient of its domain. More precisely, every surjection f : A → B can be factored as a projection followed by a bijection as follows. Let A/~ be the equivalence classes of A under the following equivalence relation: x ~ y if and only if f(x) = f(y). Equivalently, A/~ is the set of all preimages under f. Let P(~) : A → A/~ be the projection map which sends each x in A to its equivalence class [x]~, and let fP : A/~ → B be the well-defined function given by fP([x]~) = f(x). Then f = fP o P(~). A dual factorisation is given for injections above.
- The composition of two surjections is again a surjection, but if g o f is surjective, then it can only be concluded that g is surjective. See the figure at right*.
Bijection

If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
every possible image is mapped to by exactly one argument. This equivalent condition is formally expressed as follows.
- The function
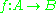 is bijective iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
is bijective iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
for all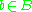 , there is a unique
, there is a unique 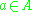 such that
such that 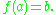
- A function f : A → B is bijective if and only if it is invertible, that is, there is a function g: B → A such that g o f = identity function on A and f o g = identity function on B. This function maps each image to its unique preimage.
- The composition of two bijections is again a bijection, but if g o f is a bijection, then it can only be concluded that f is injective and g is surjective. (See the figure at right and the remarks above regarding injections and surjections.)
- The bijections from a set to itself form a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition, called the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
Cardinality
Suppose you want to define what it means for two sets to "have the same number of elements". One way to do this is to say that two sets "have the same number of elements" if and only if all the elements of one set can be paired with the elements of the other, in such a way that each element is paired with exactly one element. Accordingly, we can define two sets to "have the same number of elements" if there is a bijection between them. We say that the two sets have the same cardinality.Likewise, we can say that set
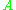 "has fewer than or the same number of elements" as set
"has fewer than or the same number of elements" as set 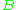 if there is an injection from
if there is an injection from 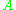 to
to 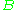 . We can also say that set
. We can also say that set 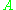 "has fewer than the number of elements" in set
"has fewer than the number of elements" in set 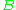 if there is an injection from
if there is an injection from 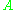 to
to 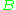 but not a bijection between
but not a bijection between 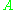 and
and 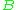 .
.Examples
It is important to specify the domain and codomain of each function since by changing these, functions which we think of as the same may have different jectivity.Injective and surjective (bijective)
- For every set A the identity function idA and thus specifically
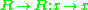 .
. -
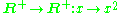 and thus also its inverse
and thus also its inverse 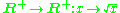 .
. - The exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
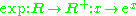 and thus also its inverse the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
and thus also its inverse the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
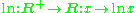
Injective and non-surjective
- The exponential function
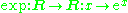
Non-injective and surjective
Non-injective and non-surjective
Properties
- For every function f, subset A of the domain and subset B of the codomain we have A ⊂ f −1(f(A)) and f(f −1(B)) ⊂ B. If f is injective we have A = f −1(f(A)) and if f is surjective we have f(f −1(B)) = B.
- For every function h : A → C we can define a surjection H : A → h(A) : a → h(a) and an injection I : h(A) → C : a → a. It follows that h = I ∘ H. This decomposition is unique up to isomorphism.
Category theory
In the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of sets, injections, surjections, and bijections correspond precisely to monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s, epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s, and isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s, respectively.