Vector-valued function
Encyclopedia
A vector-valued function also referred to as a vector function is a mathematical function
of one or more variables whose range
is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector. The dimension of the domain is not defined by the dimension of the range.
parameter t, often representing time
, producing a vector v(t) as the result. In terms of the standard unit vectors i, j, k of Cartesian 3-space, these specific type of vector-valued functions are given by expressions such as
where f(t), g(t) and h(t) are the coordinate functions of the parameter
t. The vector r(t) has its tail at the origin and its head at the coordinates evaluated by the function.
The vector shown in the graph to the right is the evaluation of the function near t=19.5 (between 6π and 6.5π; i.e., somewhat more than 3 rotations). The spiral is the path traced by the tip of the vector as t increases from zero through 8π.
Vector functions can also be referred to in a different notation:
of a vector-valued function is the intersection
of the domain of the functions f, g, and h.
by simply differentiating the components in the Cartesian coordinate system. Thus, if
is a vector-valued function, then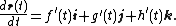
The vector derivative admits the following physical interpretation: if r(t) represents the position of a particle, then the derivative is the velocity
of the particle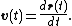
Likewise, the derivative of the velocity is the acceleration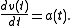
of a vector function a with respect to a scalar variable q is defined as
where ai is the scalar component of a in the direction of ei. It is also called the direction cosine of a and ei or their dot product. The vectors e1,e2,e3 form an orthonormal basis
fixed in the reference frame
in which the derivative is being taken.
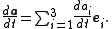
, as
Some authors prefer to use capital D to indicate the total derivative operator, as in D/Dt. The total derivative differs from the partial time derivative in that the total derivative accounts for changes in a due to the time variance of the variables qr.
, to take the derivative of a vector-valued function requires the choice of a reference frame (at least when a fixed Cartesian coordinate system is not implied as such). Once a reference frame has been chosen, the derivative of a vector-valued function can be computed using techniques similar to those for computing derivatives of scalar-valued functions. A different choice of reference frame will, in general, produce a different derivative function. The derivative functions in different reference frames have a specific kinematical relationship.
s in a fixed coordinate system, or for simple problems in physics. However, many complex problems involve the derivative of a vector function in multiple moving reference frames, which means that the basis vectors will not necessarily be constant. In such a case where the basis vectors e1,e2,e3 are fixed in reference frame E, but not in reference frame N, the more general formula for the ordinary time derivative of a vector in reference frame N is
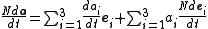
where the superscript N to the left of the derivative operator indicates the reference frame in which the derivative is taken. As shown previously, the first term on the right hand side is equal to the derivative of a in the reference frame where e1,e2,e3 are constant, reference frame E. It also can be shown that the second term on the right hand side is equal to the relative angular velocity
of the two reference frames cross multiplied with the vector a itself. Thus, after substitution, the formula relating the derivative of a vector function in two reference frames is
where NωE is the angular velocity
of the reference frame E relative to the reference frame N.
One common example where this formula is used is to find the velocity
of a space-borne object, such as a rocket
, in the inertial reference frame using measurements of the rocket's velocity relative to the ground. The velocity NvR in inertial reference frame N of a rocket R located at position rR can be found using the formula
where NωE is the angular velocity
of the Earth relative to the inertial frame N. Since velocity
is the derivative
of position, NvR and EvR are the derivatives of rR in reference frames N and E, respectively. By substitution,
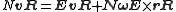
where EvR is the velocity vector of the rocket as measured from a reference frame E that is fixed to the Earth.
of scalar functions. Specifically, in the case of scalar multiplication of a vector, if p is a scalar variable function of q,
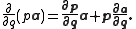
In the case of dot multiplication, for two vectors a and b that are both functions of q,
Similarly, the derivative of the cross product of two vector functions is
can be written as 
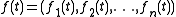. Its derivative equals
.
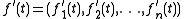If f is a function of several variables, say of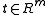
, then the partial derivatives of the components of f form a 
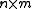matrix called the Jacobian matrix of f.
,
then f may be called an infinite-dimensional vector function.
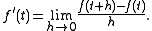
Most results of the finite-dimensional case also hold in the infinite-dimensional case too, mutatis mutandis. Differentiation can also be defined to functions of several variables (e.g.,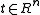
or even 
, where Y is an infinite-dimensional vector space).
N.B. If X is a Hilbert space, then one can easily show that any derivative (and any other limit) can be computed componentwise: if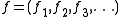
(i.e.,
, where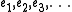 
is an orthonormal basis
of the space X), and
exists, then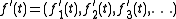
.
However, the existence of a componentwise derivative does not guarantee the existence of a derivative, as componentwise convergence in a Hilbert space does not guarantee convergence with respect to the actual topology of the Hilbert space.
s X too. However, not as many classical results hold in the Banach space
setting, e.g., an absolutely continuous function with values in a suitable Banach space need not have a derivative anywhere. Moreover, in most Banach spaces setting there are no orthonormal bases.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of one or more variables whose range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector. The dimension of the domain is not defined by the dimension of the range.
Example
A common example of a vector valued function is one that depends on a single real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
parameter t, often representing time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, producing a vector v(t) as the result. In terms of the standard unit vectors i, j, k of Cartesian 3-space, these specific type of vector-valued functions are given by expressions such as
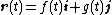or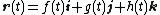
where f(t), g(t) and h(t) are the coordinate functions of the parameter
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
t. The vector r(t) has its tail at the origin and its head at the coordinates evaluated by the function.
The vector shown in the graph to the right is the evaluation of the function near t=19.5 (between 6π and 6.5π; i.e., somewhat more than 3 rotations). The spiral is the path traced by the tip of the vector as t increases from zero through 8π.
Vector functions can also be referred to in a different notation:
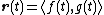or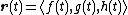
Properties
The domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of a vector-valued function is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the domain of the functions f, g, and h.
Derivative of a three-dimensional vector function
Many vector-valued functions, like scalar-valued functions, can be differentiatedDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
by simply differentiating the components in the Cartesian coordinate system. Thus, if
is a vector-valued function, then
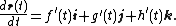
The vector derivative admits the following physical interpretation: if r(t) represents the position of a particle, then the derivative is the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the particle
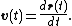
Likewise, the derivative of the velocity is the acceleration
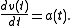
Partial derivative
The partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of a vector function a with respect to a scalar variable q is defined as
where ai is the scalar component of a in the direction of ei. It is also called the direction cosine of a and ei or their dot product. The vectors e1,e2,e3 form an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
fixed in the reference frame
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
in which the derivative is being taken.
Ordinary derivative
If a is regarded as a vector function of a single scalar variable, such as time t, then the equation above reduces to the first ordinary time derivative of a with respect to t,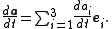Total derivative
If the vector a is a function of a number n of scalar variables qr (r = 1,...,n), and each qr is only a function of time t, then the ordinary derivative of a with respect to t can be expressed, in a form known as the total derivativeTotal derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
, as
Some authors prefer to use capital D to indicate the total derivative operator, as in D/Dt. The total derivative differs from the partial time derivative in that the total derivative accounts for changes in a due to the time variance of the variables qr.
Reference frames
Whereas for scalar-valued functions there is only a single possible reference frameFrame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
, to take the derivative of a vector-valued function requires the choice of a reference frame (at least when a fixed Cartesian coordinate system is not implied as such). Once a reference frame has been chosen, the derivative of a vector-valued function can be computed using techniques similar to those for computing derivatives of scalar-valued functions. A different choice of reference frame will, in general, produce a different derivative function. The derivative functions in different reference frames have a specific kinematical relationship.
Derivative of a vector function with nonfixed bases
The above formulas for the derivative of a vector function rely on the assumption that the basis vectors e1,e2,e3 are constant, that is, fixed in the reference frame in which the derivative of a is being taken, and therefore the e1,e2,e3 each has a derivative of identically zero. This often holds true for problems dealing with vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s in a fixed coordinate system, or for simple problems in physics. However, many complex problems involve the derivative of a vector function in multiple moving reference frames, which means that the basis vectors will not necessarily be constant. In such a case where the basis vectors e1,e2,e3 are fixed in reference frame E, but not in reference frame N, the more general formula for the ordinary time derivative of a vector in reference frame N is
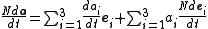
where the superscript N to the left of the derivative operator indicates the reference frame in which the derivative is taken. As shown previously, the first term on the right hand side is equal to the derivative of a in the reference frame where e1,e2,e3 are constant, reference frame E. It also can be shown that the second term on the right hand side is equal to the relative angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the two reference frames cross multiplied with the vector a itself. Thus, after substitution, the formula relating the derivative of a vector function in two reference frames is
where NωE is the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the reference frame E relative to the reference frame N.
One common example where this formula is used is to find the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of a space-borne object, such as a rocket
Rocket
A rocket is a missile, spacecraft, aircraft or other vehicle which obtains thrust from a rocket engine. In all rockets, the exhaust is formed entirely from propellants carried within the rocket before use. Rocket engines work by action and reaction...
, in the inertial reference frame using measurements of the rocket's velocity relative to the ground. The velocity NvR in inertial reference frame N of a rocket R located at position rR can be found using the formula
where NωE is the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the Earth relative to the inertial frame N. Since velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of position, NvR and EvR are the derivatives of rR in reference frames N and E, respectively. By substitution,
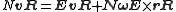
where EvR is the velocity vector of the rocket as measured from a reference frame E that is fixed to the Earth.
Derivative and vector multiplication
The derivative of the products of vector functions behaves similarly to the derivative of the productsProduct rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
of scalar functions. Specifically, in the case of scalar multiplication of a vector, if p is a scalar variable function of q,
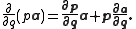
In the case of dot multiplication, for two vectors a and b that are both functions of q,
Similarly, the derivative of the cross product of two vector functions is
Derivative of an n-dimensional vector function
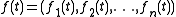A function f of a real number t with values in the space can be written as . Its derivative equals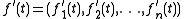.If f is a function of several variables, say of
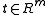, then the partial derivatives of the components of f form a 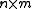matrix called the Jacobian matrix of f.Infinite-dimensional vector functions
If the values of a function f lie in an infinite-dimensional vector space X, such as a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
,
then f may be called an infinite-dimensional vector function.
Functions with values in a Hilbert space
If the argument of f is a real number and X is a a Hilbert space, then the derivative of f at a point t can be defined as in the finite-dimensional case: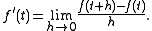Most results of the finite-dimensional case also hold in the infinite-dimensional case too, mutatis mutandis. Differentiation can also be defined to functions of several variables (e.g.,
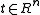or even , where Y is an infinite-dimensional vector space).N.B. If X is a Hilbert space, then one can easily show that any derivative (and any other limit) can be computed componentwise: if
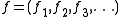
(i.e.,
, where 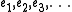is an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the space X), and
exists, then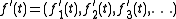.However, the existence of a componentwise derivative does not guarantee the existence of a derivative, as componentwise convergence in a Hilbert space does not guarantee convergence with respect to the actual topology of the Hilbert space.
Other infinite-dimensional vector spaces
Most of the above hold for other topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s X too. However, not as many classical results hold in the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
setting, e.g., an absolutely continuous function with values in a suitable Banach space need not have a derivative anywhere. Moreover, in most Banach spaces setting there are no orthonormal bases.
See also
- Infinite-dimensional-vector function
- Coordinate vectorCoordinate vectorIn linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
- Vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
- CurveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
- Parametric surfaceParametric surfaceA parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
- Position vector
- ParametrizationParametrizationParametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....