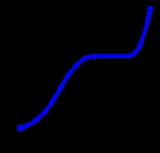
Monotonic function - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a monotonic function (or monotone function) is a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

that preserves the given order

Order (mathematics)

Order in mathematics may refer to:-In algebra:*Order , the cardinality of a group or period of an element*Order, or degree of a polynomial*Order, or dimension of a matrix*Order , an algebraic structure*Ordered group...

. This concept first arose in calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

, and was later generalized to the more abstract setting of order theory

Order theory

Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...

Monotonicity in calculus and analysis

In calculus

Calculus

, a function f defined on a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

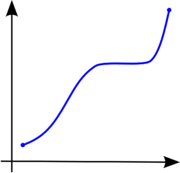
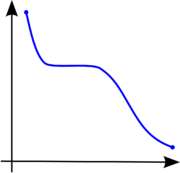
of the real numbers with real values is called monotonic (also monotonically increasing, increasing or non-decreasing), if for all x and y such that x ≤ y one has f(x) ≤ f(y), so f preserves the order (see Figure 1). Likewise, a function is called monotonically decreasing (also decreasing, or non-increasing) if, whenever x ≤ y, then f(x) ≥ f(y), so it reverses the order (see Figure 2).

If the order ≤ in the definition of monotonicity is replaced by the strict order <, then one obtains a stronger requirement. A function with this property is called strictly increasing. Again, by inverting the order symbol, one finds a corresponding concept called strictly decreasing. Functions that are strictly increasing or decreasing are one-to-one (because for x not equal to y, either x < y or x > y and so, by monotonicity, either f(x) < f(y) or f(x) > f(y), thus f(x) is not equal to f(y)).

When functions between discrete sets are considered in combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

, it is not always obvious that "increasing" and "decreasing" are taken to include the possibility of repeating the same value at successive arguments, so one finds the terms weakly increasing and weakly decreasing to stress this possibility.

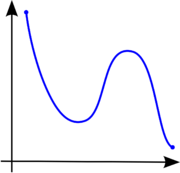
The terms "non-decreasing" and "non-increasing" should not be confused with the (much weaker) negative qualifications "not decreasing" and "not increasing". For example, the function of figure 3 first falls, then rises, then falls again. It is therefore not decreasing and not increasing, but it is neither non-decreasing nor non-increasing.

The term monotonic transformation can also possibly cause some confusion because it refers to a transformation by a strictly increasing function. Notably, this is the case in economics with respect to the ordinal properties of a utility function being preserved across a monotonic transform (see also monotone preferences

Monotone preferences

In economics, an agent's preferences are said to be weakly monotonic if, given a consumption bundle x, the agent prefers all consumption bundles y that have more of every good. That is, y \gg x implies y\succ x. An agent's preferences are said to be strongly monotonic if, given a consumption...

).

A function f(x) is said to be absolutely monotonic over an interval (a, b) if the derivatives of all orders of f are nonnegative at all points on the interval.

Some basic applications and results

The following properties are true for a monotonic function f : R → R:

f has limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

from the right and from the left at every point of its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

;
f has a limit at infinity (either ∞ or −∞) of either a real number, ∞, or −∞.
f can only have jump discontinuities;
f can only have countably many discontinuities in its domain.

These properties are the reason why monotonic functions are useful in technical work in analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

. Two facts about these functions are:

if f is a monotonic function defined on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

I, then f is differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

on I, i.e. the set of numbers x in I such that f is not differentiable in x has Lebesgue
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

measure zero.
if f is a monotonic function defined on an interval [a, b], then f is Riemann integrable
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...

.

An important application of monotonic functions is in probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

. If X is a random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

, its cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

F_X(x) = Prob(X ≤ x)

is a monotonically increasing function.

A function is unimodal if it is monotonically increasing up to some point (the mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....

) and then monotonically decreasing.

Monotonicity in functional analysis

In functional analysis

Functional analysis

Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...

on a topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

X, a (possibly non-linear) operator T : X → X^∗ is said to be a monotone operator if

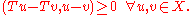
Kachurovskii's theorem

In mathematics, Kachurovskii's theorem is a theorem relating the convexity of a function on a Banach space to the monotonicity of its Fréchet derivative.-Statement of the theorem:...

shows that convex function

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

s on Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

s have monotonic operators as their derivatives.

A subset G of X × X^∗ is said to be a monotone set if for every pair [u₁,w₁] and [u₂,w₂] in G,

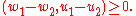
G is said to be maximal monotone if it is maximal among all monotone sets in the sense of set inclusion. The graph of a monotone operator G(T) is a monotone set. A monotone operator is said to be maximal monotone if its graph is a maximal monotone set.

Monotonicity in order theory

In order theory, one does not restrict to real numbers, but one is concerned with arbitrary partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

s or even with preordered sets

Preorder

In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...

. In these cases, the above definition of monotonicity is relevant as well. However, the terms "increasing" and "decreasing" are avoided, since they lose their appealing pictorial motivation as soon as one deals with orders that are not total

Total order

In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

. Furthermore, the strict relations < and > are of little use in many non-total orders and hence no additional terminology is introduced for them.

A monotone function is also called isotone, or . The dual

Duality (order theory)

In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...

notion is often called antitone, anti-monotone, or order-reversing. Hence, an antitone function f satisfies the property

x ≤ y implies f(x) ≥ f(y),

for all x and y in its domain. It is easy to see that the composite of two monotone mappings is also monotone.

A constant function

Constant function

In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...

is both monotone and antitone; conversely, if f is both monotone and antitone, and if the domain of f is a lattice

Lattice (order)

In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...

, then f must be constant.

Monotone functions are central in order theory. They appear in most articles on the subject and examples from special applications are found in these places. Some notable special monotone functions are order embeddings (functions for which x ≤ y if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

f(x) ≤ f(y)) and order isomorphism

Order isomorphism

In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...

s (surjective order embeddings).

Monotonicity in computer science

In computer science, monotonicity (also called consistency) is a condition applied to heuristic function

Heuristic function

A heuristic function, or simply a heuristic, is a function that ranks alternatives in various search algorithms at each branching step based on the available information in order to make a decision about which branch to follow during a search.-Shortest paths:For example, for shortest path...

s. A heuristic h(n) is monotonic if, for every node n and every successor n of n generated by any action a, the estimated cost of reaching the goal from n is no greater than the step cost of getting to n' plus the estimated cost of reaching the goal from n' ,

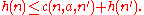
This is a form of triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

, with n, n, and the goal G_n closest to n. Because every monotonic heuristic is also admissible

Admissible heuristic

In computer science, specifically in algorithms related to Pathfinding, a heuristic function is said to be admissible if it is no more than the lowest-cost path to the goal. In other words, a heuristic is admissible if it never overestimates the cost of reaching the goal...

, monotonicity is a stricter requirement than admissibility. In some heuristic algorithms, such as A*, the algorithm can be considered optimal if it is monotonic.

Boolean functions

In Boolean algebra, a monotonic function is one such that for all a_i and b_i in {0,1}, if a₁ ≤ b₁, a₂ ≤ b₂, ..., a_n ≤ b_n, then f(a₁, ... , a_n) ≤ f(b₁, ... , b_n). In other words, a Boolean function is monotonic if, for every combination of inputs, switching one of the inputs from false to true can only cause the output to switch from false to true and not from true to false. Graphically, this means that a Boolean function is monotonic when in its Hasse diagram

Hasse diagram

In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...

(dual of its Venn diagram

Venn diagram

Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...

), there is no 1 (red vertex) connected to a higher 0 (white vertex).

The monotonic Boolean functions are precisely those that can be defined by an expression combining the inputs (which may appear more than once) using only the operators and
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....

and or
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...

(in particular not
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...

is forbidden). For instance "at least two of a,b,c hold" is a monotonic function of a,b,c, since it can be written for instance as ((a and b) or (a and c) or (b and c)).

The number of such functions on n variables is known as the Dedekind number

Dedekind number

Image:Monotone Boolean functions 0,1,2,3.svg|400px|thumb|right| The free distributive lattices of monotonic Boolean functions on 0, 1, 2, and 3 arguments, with 2, 3, 6, and 20 elements respectively...

of n.

Monotonic logic

Monotonicity of entailment

Entailment

In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...

is a property of many logic systems that states that the hypotheses of any derived fact may be freely extended with additional assumptions. Any true statement in a logic with this property continues to be true, even after adding new axiom

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

s. Logics with this property may be called monotonic, to differentiate them from non-monotonic logic

Non-monotonic logic

A non-monotonic logic is a formal logic whose consequence relation is not monotonic. Most studied formal logics have a monotonic consequence relation, meaning that adding a formula to a theory never produces a reduction of its set of consequences. Intuitively, monotonicity indicates that learning a...

External links

Convergence of a Monotonic Sequence by Anik Debnath and Thomas Roxlo (The Harker School), Wolfram Demonstrations Project
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

.
Definition of a Monotonic function from Wolfram Alpha
Wolfram Alpha
Wolfram Alpha is an answer-engine developed by Wolfram Research. It is an online service that answers factual queries directly by computing the answer from structured data, rather than providing a list of documents or web pages that might contain the answer as a search engine might...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.