Mu-recursive function - AbsoluteAstronomy.com

Mathematical logic

Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...

and computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, the μ-recursive functions are a class of partial function

Partial function

In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...

s from natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s to natural number

Natural number

s which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that can be computed by Turing machine

Turing machine

A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...

s. The μ-recursive functions are closely related to primitive recursive function

Primitive recursive function

The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...

s, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every μ-recursive function is a primitive recursive function — the most famous example is the Ackermann function

Ackermann function

In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...

.

Other equivalent classes of functions are the λ-recursive functions and the functions that can be computed by Markov algorithm

Markov algorithm

In theoretical computer science, a Markov algorithm is a string rewriting system that uses grammar-like rules to operate on strings of symbols. Markov algorithms have been shown to be Turing-complete, which means that they are suitable as a general model of computation and can represent any...

s.

The set of all recursive functions is known as R

R (complexity)

In computational complexity theory, R is the class of decision problems solvable by a Turing machine, which is the set of all recursive languages. R is equal to the set of all total computable functions....

in computational complexity theory

Computational complexity theory

Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...

Definition

The μ-recursive functions (or partial μ-recursive functions) are partial functions that take finite tuples of natural numbers and return a single natural number. They are the smallest class of partial functions that includes the initial functions and is closed under composition, primitive recursion, and the μ operator.

The smallest class of functions including the initial functions and closed under composition and primitive recursion (i.e. without minimisation) is the class of primitive recursive functions. While all primitive recursive functions are total, this is not true of partial recursive functions; for example, the minimisation of the successor function is undefined. The set of total recursive functions is a subset of the partial recursive functions and is a superset of the primitive recursive functions; functions like the Ackermann function

Ackermann function

can be proven to be total recursive, and not primitive.

The first three functions are called the "initial" or "basic" functions: (In the following the subscripting is per Kleene (1952) p. 219. For more about some of the various symbolisms found in the literature see Symbolism below.)

Constant function: For each natural number and every :

.

Alternative definitions use compositions of the successor function and use a zero function, that always returns zero, in place of the constant function.
Successor function S:
Projection function 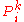(also called the Identity function 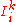): For all natural numbers such that :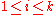

.
Composition operator (also called the substitution operator): Given an m-ary function and m k-ary functions :

.
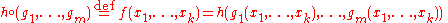Primitive recursion operator 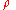: Given the k-ary function and k+2 -ary function :
.
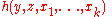1. Minimisation operator 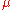: Given a (k+1)-ary total function :
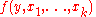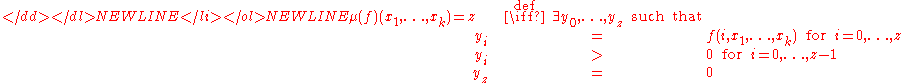
  Intuitively, minimisation seeks--beginning the search from 0 and proceeding upwards--the smallest argument that causes the function to return zero; if there is no such argument, the search never terminates.
  
  The strong equality operator can be used to compare partial μ-recursive functions. This is defined for all partial functions f and g so that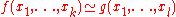
  holds if and only if for any choice of arguments either both functions are defined and their values are equal or both functions are undefined.
  
  Equivalence with other models of computability
  In the equivalence of models of computability, a parallel is drawn between Turing machine
  Turing machine
  A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
  
  s which do not terminate for certain inputs and an undefined result for that input in the corresponding partial recursive function.
  The unbounded search operator is not definable by the rules of primitive recursion as those do not provide a mechanism for "infinite loops" (undefined values).
  
  Normal form theorem
  A normal form theorem due to Kleene says that for each k there are primitive recursive functions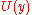 and 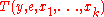such that for any μ-recursive function with k free variables there is an e such that.
  The number e is called an index or Gödel number for the function f. A consequence of this result is that any μ-recursive function can be defined using a single instance of the μ operator applied to a (total) primitive recursive function.
  
  Minsky (1967) observes (as does Boolos-Burgess-Jeffrey (2002) pp. 94–95) that the U defined above is in essence the μ-recursive equivalent of the universal Turing machine
  Universal Turing machine
  In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
  
  :
  
  To construct U is to write down the definition of a general-recursive function U(n, x) that correctly interprets the number n and computes the appropriate function of x. to construct U directly would involve essentially the same amount of effort, and essentially the same ideas, as we have invested in constructing the universal Turing machine. (italics in original, Minsky (1967) p. 189)
  
  Symbolism
  A number of different symbolisms are used in the literature. An advantage to using the symbolism is a derivation of a function by "nesting" of the operators one inside the other is easier to write in a compact form. In the following we will abbreviate the string of parameters x₁, ..., x_n as x:
  
  Constant function: Kleene uses " C_qⁿ(x) = q " and Boolos-Burgess-Jeffry (2002) (B-B-J) use the abbreviation " const_n( x) = n ":
  
  e.g. C₁₃⁷ ( r, s, t, u, v, w, x ) = 13
  
  e.g. const₁₃ ( r, s, t, u, v, w, x ) = 13
  
  Successor function: Kleene uses x' and S for "Successor". As "successor" is considered to be primitive, most texts use the apostrophe as follows:
  
  S(a) = a +1 =_def a', where 1 =_def 0', 2 =_def 0 ' ', etc.
  
  Identity function: Kleene (1952) uses " U_iⁿ " to indicate the identity function over the variables x_i; B-B-J use the identity function id_iⁿ over the variables x₁ to x_n:
  
  U_iⁿ( x ) = id_iⁿ( x ) = x_i
  
  e.g. U₃⁷ = id₃⁷ ( r, s, t, u, v, w, x ) = t
  
  Composition (Substitution) operator: Kleene uses a bold-face S_n^m (not to be confused with his S for "successor" ! ). The superscript "m" refers to the m^th of function "f_m", whereas the subscript "n" refers to the n^th variable "x_n":
  
  If we are given h( x )= g( f₁(x), ... , f_m(x) )
  
  h(x) = S_mⁿ(g, f₁, ... , f_m )
  
  In a similar manner, but without the sub- and superscripts, B-B-J write:
  
  h(x)= Cn[g, f₁ ,..., f_m](x)
  
  Primitive Recursion: Kleene uses the symbol " Rⁿ(base step, induction step) " where n indicates the number of variables, B-B-J use " Pr(base step, induction step)(x)". Given:
  
  base step: h( 0, x )= f( x ), and
  
  induction step: h( y+1, x ) = g( y, h(x,y),x )
  
  Example: primitive recursion definition of a + b:
  
  base step: f( 0, a ) = a = U₁¹(a)
  
  induction step: f( b' , a ) = ( f ( b, a ) )' = g( b, f( b, a), a ) = g( b, c, a ) = c' = S(U₂³( b, c, a )
  
  R² { U₁¹(a), S [ (U₂³( b, c, a ) ] }
  
  Pr{ U₁¹(a), S[ (U₂³( b, c, a ) ] }
  
  Example: Kleene gives an example of how to perform the recursive derivation of f(b, a) = b + a (notice reversal of variables a and b). He starting with 3 initial functions
  
  S(a) = a'
  
  U₁¹(a) = a
  
  U₂³( b, c, a ) = c
  
  g(b, c, a) = S(U₂³( b, c, a )) = c'
  
  base step: h( 0, a ) = U₁¹(a)
  
  induction step: h( b', a ) = g( b, h( b, a ), a )
  
  He arrives at:
  
  a+b = R²[ U₁¹, S₁³(S, U₂³) ]
  
  External links
  
  Stanford Encyclopedia of Philosophy entry
  
  The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Definition

Equivalence with other models of computability

Normal form theorem

Symbolism

External links