Cardinality
Encyclopedia
In mathematics
, the cardinality of a set is a measure of the "number of elements of the set". For example, the set A = {2, 4, 6} contains 3 elements, and therefore A has a cardinality of 3. There are two approaches to cardinality – one which compares sets directly using bijection
s and injection
s, and another which uses cardinal number
s.
The cardinality of a set A is usually denoted | A |, with a vertical bar
on each side; this is the same notation as absolute value
and the meaning depends on context
. Alternatively, the cardinality of a set A may be denoted by n(A), A, or # A.
The relation of having the same cardinality is called equinumerosity
, and this is an equivalence relation
on the class
of all sets. The equivalence class of a set A under this relation then consists of all those sets which have the same cardinality as A. There are two ways to define the "cardinality of a set":
The cardinalities of the infinite sets are denoted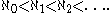
For each ordinal
α, α + 1 is the least cardinal number greater than α.
The cardinality of the natural number
s is denoted aleph-null
(0), while the cardinality of the real number
s is denoted by c, and is also referred to as the cardinality of the continuum
. We can show that c = 20; this also being the cardinality of the set of all subsets of the natural numbers. The continuum hypothesis
says that 1 = 20, i.e. 20 is the smallest cardinal number bigger than 0, i.e. there is no set whose cardinality is strictly between that of the integers and that of the real numbers. The continuum hypothesis still remains unresolved in an "absolute" sense. See below for more details on the cardinality of the continuum.
, Gottlob Frege
, Richard Dedekind
and others rejected the view of Galileo (which derived from Euclid
) that the whole cannot be the same size as the part. One example of this is Hilbert's paradox of the Grand Hotel
.
The reason for this is that the various characterizations of what it means for set A to be larger than set B, or to be the same size as set B, which are all equivalent for finite sets, are no longer equivalent for infinite sets. Different characterizations can yield different results. For example, in the popular characterization of size chosen by Cantor, sometimes an infinite set A is larger (in that sense) than an infinite set B; while other characterizations may yield that an infinite set A is always the same size as an infinite set B.
For finite sets, counting is just forming a bijection
(i.e., a one-to-one correspondence) between the set being counted and an initial segment of the positive integers. Thus there is no notion equivalent to counting for infinite sets. While counting gives a unique result when applied to a finite set, an infinite set may be placed into a one-to-one correspondence with many different ordinal numbers depending on how one chooses to "count" (order) it.
Additionally, different characterizations of size, when extended to infinite sets, will break different "rules" which held for finite sets. Which rules are broken varies from characterization to characterization. For example, Cantor's characterization, while preserving the rule that sometimes one set is larger than another, breaks the rule that deleting an element makes the set smaller. Another characterization may preserve the rule that deleting an element makes the set smaller, but break another rule. Furthermore, some characterization may not "directly" break a rule, but it may not "directly" uphold it either, in the sense that whichever is the case depends upon a controversial axiom such as the axiom of choice or the continuum hypothesis. Thus there are three possibilities. Each characterization will break some rules, uphold some others, and may be indecisive about some others.
If one extends to multiset
s, further rules are broken (assuming Cantor's approach), which hold for finite multisets. If we have two multisets A and B, A not being larger than B and B not being larger than A does not necessarily imply A has the same size as B. This rule holds for multisets that are finite. Needless to say, the law of trichotomy is explicitly broken in this case, as opposed to the situation with sets, where it is equivalent to the axiom of choice.
Dedekind simply defined an infinite set as one having the same size (in Cantor's sense) as at least one of its proper parts; this notion of infinity is called Dedekind infinite. This definition only works in the presence of some form of the axiom of choice, however, so will not be considered to work by some mathematicians.
Cantor introduced the above-mentioned cardinal numbers, and showed that (in Cantor's sense) some infinite sets are greater than others. The smallest infinite cardinality is that of the natural numbers (0).
(
) is greater than that of the natural numbers (0); that is, there are more real numbers R than whole numbers N. Namely, Cantor showed that
.
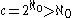The continuum hypothesis
states that there is no cardinal number
between the cardinality of the reals and the cardinality of the natural numbers, that is,
.
However, this hypothesis can neither be proved nor disproved within the widely accepted ZFC axiomatic set theory, if ZFC is consistent.
Cardinal arithmetic can be used to show not only that the number of points in a real number line is equal to the number of points in any segment
of that line, but that this is equal to the number of points on a plane and, indeed, in any finite-dimensional space. These results are highly counterintuitive, because they imply that there exist proper subsets and proper supersets of an infinite set S that have the same size as S, although S contains elements that do not belong to its subsets, and the supersets of S contain elements that are not included in it.
The first of these results is apparent by considering, for instance, the tangent function, which provides a one-to-one correspondence between the interval
(−½π, ½π) and R (see also Hilbert's paradox of the Grand Hotel
).
The second result was first demonstrated by Cantor in 1878, but it became more apparent in 1890, when Giuseppe Peano
introduced the space-filling curve
s, curved lines that twist and turn enough to fill the whole of any square, or cube, or hypercube
, or finite-dimensional space. These curves are not a direct proof that a line has the same number of points as a finite-dimensional space, but they can be easily used to obtain such a proof.
Cantor also showed that sets with cardinality strictly greater than
exist (see his generalized diagonal argument and theorem
). They include, for instance:
Both have cardinality
.
The cardinal equalities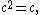
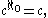and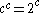 
can be demonstrated using cardinal arithmetic: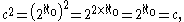
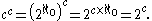
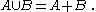
From this, one can show that in general the cardinalities of unions
and intersections
are related by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the cardinality of a set is a measure of the "number of elements of the set". For example, the set A = {2, 4, 6} contains 3 elements, and therefore A has a cardinality of 3. There are two approaches to cardinality – one which compares sets directly using bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s and injection
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
s, and another which uses cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s.
The cardinality of a set A is usually denoted | A |, with a vertical bar
Vertical bar
The vertical bar is a character with various uses in mathematics, where it can be used to represent absolute value, among others; in computing and programming and in general typography, as a divider not unlike the interpunct...
on each side; this is the same notation as absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
and the meaning depends on context
Ambiguity
Ambiguity of words or phrases is the ability to express more than one interpretation. It is distinct from vagueness, which is a statement about the lack of precision contained or available in the information.Context may play a role in resolving ambiguity...
. Alternatively, the cardinality of a set A may be denoted by n(A), A, or # A.
Case 1: | A | = | B |
- Two sets A and B have the same cardinality if there exists a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, that is, an injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and surjective functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, from A to B.
- For example, the set E = {0, 2, 4, 6, ...} of non-negative even numbers has the same cardinality as the set N = {0, 1, 2, 3, ...} of natural numbers, since the function f(n) = 2n is a bijection from N to E.
Case 2: | A | ≥ | B |
- A has cardinality greater than or equal to the cardinality of B if there exists an injective function from B into A.
Case 3: | A | > | B |
- A has cardinality strictly greater than the cardinality of B if there is an injective function, but no bijective function, from B to A.
- For example, the set R of all real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s has cardinality strictly greater than the cardinality of the set N of all natural numbers, because the inclusion map i : N → R is injective, but it can be shown that there does not exist a bijective function from N to R (see Cantor's diagonal argumentCantor's diagonal argumentCantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
or Cantor's first uncountability proofCantor's first uncountability proofGeorg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
).
Cardinal numbers
Above, "cardinality" was defined functionally. That is, the "cardinality" of a set was not defined as a specific object itself. However, such an object can be defined as follows.The relation of having the same cardinality is called equinumerosity
Equinumerosity
In mathematics, two sets are equinumerous if they have the same cardinality, i.e., if there exists a bijection f : A → B for sets A and B. This is usually denoted A \approx B \, or A \sim B....
, and this is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all sets. The equivalence class of a set A under this relation then consists of all those sets which have the same cardinality as A. There are two ways to define the "cardinality of a set":
- The cardinality of a set A is defined as its equivalence class under equinumerosity.
- A representative set is designated for each equivalence class. The most common choice is the initial ordinal in that classVon Neumann cardinal assignmentThe von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...
. This is usually taken as the definition of cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
in axiomatic set theory.
The cardinalities of the infinite sets are denoted
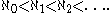
For each ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
α, α + 1 is the least cardinal number greater than α.
The cardinality of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is denoted aleph-null
Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
(0), while the cardinality of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is denoted by c, and is also referred to as the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. We can show that c = 20; this also being the cardinality of the set of all subsets of the natural numbers. The continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
says that 1 = 20, i.e. 20 is the smallest cardinal number bigger than 0, i.e. there is no set whose cardinality is strictly between that of the integers and that of the real numbers. The continuum hypothesis still remains unresolved in an "absolute" sense. See below for more details on the cardinality of the continuum.
Finite, countable and uncountable sets
If the axiom of choice holds, the law of trichotomy holds for cardinality. Thus we can make the following definitions:- Any set X with cardinality less than that of the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, or | X | < | N |, is said to be a finite set. - Any set X that has the same cardinality as the set of the natural numbers, or | X | = | N | = 0, is said to be a countably infiniteCountable setIn mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
set. - Any set X with cardinality greater than that of the natural numbers, or | X | > | N |, for example | R | = c > | N |, is said to be uncountableUncountable setIn mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
.
Infinite sets
Our intuition gained from finite sets breaks down when dealing with infinite sets. In the late nineteenth century Georg CantorGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, Gottlob Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
, Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
and others rejected the view of Galileo (which derived from Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
) that the whole cannot be the same size as the part. One example of this is Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...
.
The reason for this is that the various characterizations of what it means for set A to be larger than set B, or to be the same size as set B, which are all equivalent for finite sets, are no longer equivalent for infinite sets. Different characterizations can yield different results. For example, in the popular characterization of size chosen by Cantor, sometimes an infinite set A is larger (in that sense) than an infinite set B; while other characterizations may yield that an infinite set A is always the same size as an infinite set B.
For finite sets, counting is just forming a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
(i.e., a one-to-one correspondence) between the set being counted and an initial segment of the positive integers. Thus there is no notion equivalent to counting for infinite sets. While counting gives a unique result when applied to a finite set, an infinite set may be placed into a one-to-one correspondence with many different ordinal numbers depending on how one chooses to "count" (order) it.
Additionally, different characterizations of size, when extended to infinite sets, will break different "rules" which held for finite sets. Which rules are broken varies from characterization to characterization. For example, Cantor's characterization, while preserving the rule that sometimes one set is larger than another, breaks the rule that deleting an element makes the set smaller. Another characterization may preserve the rule that deleting an element makes the set smaller, but break another rule. Furthermore, some characterization may not "directly" break a rule, but it may not "directly" uphold it either, in the sense that whichever is the case depends upon a controversial axiom such as the axiom of choice or the continuum hypothesis. Thus there are three possibilities. Each characterization will break some rules, uphold some others, and may be indecisive about some others.
If one extends to multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s, further rules are broken (assuming Cantor's approach), which hold for finite multisets. If we have two multisets A and B, A not being larger than B and B not being larger than A does not necessarily imply A has the same size as B. This rule holds for multisets that are finite. Needless to say, the law of trichotomy is explicitly broken in this case, as opposed to the situation with sets, where it is equivalent to the axiom of choice.
Dedekind simply defined an infinite set as one having the same size (in Cantor's sense) as at least one of its proper parts; this notion of infinity is called Dedekind infinite. This definition only works in the presence of some form of the axiom of choice, however, so will not be considered to work by some mathematicians.
Cantor introduced the above-mentioned cardinal numbers, and showed that (in Cantor's sense) some infinite sets are greater than others. The smallest infinite cardinality is that of the natural numbers (0).
Cardinality of the continuum
One of Cantor's most important results was that the cardinality of the continuumCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
(
) is greater than that of the natural numbers (0); that is, there are more real numbers R than whole numbers N. Namely, Cantor showed that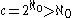.The continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
states that there is no cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
between the cardinality of the reals and the cardinality of the natural numbers, that is,
.However, this hypothesis can neither be proved nor disproved within the widely accepted ZFC axiomatic set theory, if ZFC is consistent.
Cardinal arithmetic can be used to show not only that the number of points in a real number line is equal to the number of points in any segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
of that line, but that this is equal to the number of points on a plane and, indeed, in any finite-dimensional space. These results are highly counterintuitive, because they imply that there exist proper subsets and proper supersets of an infinite set S that have the same size as S, although S contains elements that do not belong to its subsets, and the supersets of S contain elements that are not included in it.
The first of these results is apparent by considering, for instance, the tangent function, which provides a one-to-one correspondence between the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(−½π, ½π) and R (see also Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...
).
The second result was first demonstrated by Cantor in 1878, but it became more apparent in 1890, when Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
introduced the space-filling curve
Space-filling curve
In mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
s, curved lines that twist and turn enough to fill the whole of any square, or cube, or hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
, or finite-dimensional space. These curves are not a direct proof that a line has the same number of points as a finite-dimensional space, but they can be easily used to obtain such a proof.
Cantor also showed that sets with cardinality strictly greater than
exist (see his generalized diagonal argument and theoremCantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
). They include, for instance:
- the set of all subsets of R, i.e., the power set of R, written P(R) or 2R
- the set RR of all functions from R to R
Both have cardinality
.The cardinal equalities
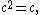
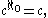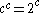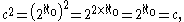
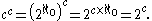
and can be demonstrated using cardinal arithmetic:Examples and properties
- If X = {a, b, c} and Y = {apples, oranges, peaches}, then | X | = | Y | because {(a, apples), (b, oranges), (c, peaches)} is a bijection between the sets X and Y. The cardinality of each of X and Y is 3.
- If | X | < | Y |, then there exists Z such that | X | = | Z | and Z ⊆ Y.
- Sets with cardinality of the continuum
Union and intersection
If A and B are disjoint sets, then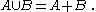From this, one can show that in general the cardinalities of unions
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
and intersections
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
are related by
See also
- Aleph numberAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
- Beth numberBeth numberIn mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
- Ordinality
- Countable setCountable setIn mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...