Gamma function - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the gamma function (represented by the capital Greek

Greek alphabet

The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...

letter Γ

Gamma

Gamma is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. It was derived from the Phoenician letter Gimel . Letters that arose from Gamma include the Roman C and G and the Cyrillic letters Ge Г and Ghe Ґ.-Greek:In Ancient Greek, gamma represented a...

) is an extension of the factorial

Factorial

In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...

function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

, with its argument shifted down by 1, to real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

and complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s. That is, if n is a positive integer:

Although the gamma function is defined for all complex numbers except the non-positive integers, it is defined via an improper integral

Improper integral

In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....

that converges only for complex numbers with a positive real part:

This integral function is extended by analytic continuation

Analytic continuation

In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...

to all complex numbers except the non-positive integers (where the function has simple poles), yielding the meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

we call the gamma function.

The gamma function is a component in various probability-distribution functions, and as such it is applicable in the fields of probability

Probability

Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

and statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, as well as combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

Motivation

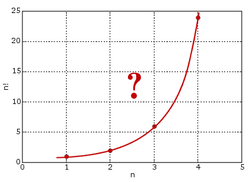
The gamma function can be seen as a solution to the following interpolation

Interpolation

In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....

problem:

"Find a smooth curve that connects the points (x, y) given by y = x! at the positive integer values for x."

A plot of the first few factorials makes clear that such a curve can be drawn, but it would be preferable to have a formula that precisely describes the curve, in which the number of operations does not depend on the size of n. The simple formula for the factorial, n! = 1 × 2 × … × n, cannot be used directly for fractional values of n since it is only valid when n is a natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

(i.e., a positive integer).
There is, in fact, no such simple solution for factorials; any combination of sums, products, powers, exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

s, or logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

s with a fixed number of terms will not suffice to express n!. However, it is possible to find a general formula for factorials using tools such as integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

s and limit

Limit of a function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

s from calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

. A good solution to this is the gamma function.

There are infinitely many continuous extensions of the factorial to non-integers: infinitely many curves can be drawn through any set of isolated points. The gamma function is the most useful solution in practice, being analytic

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

(except at the non-positive integers), and it can be characterized in several ways. However, it is not the only analytic function which extends the factorial, as adding to it any analytic function which is zero on the positive integers will give another function with that property.

A more restrictive property than satisfying the above interpolation is to satisfy the recurrence relation

Recurrence relation

In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

defining a slightly translated version of the factorial function,

for x equal to any positive real number. The Bohr–Mollerup theorem proves that these properties, together with the assumption that f be logarithmically convex (aka: "superconvex"), uniquely determine f for positive, real inputs. From there, the gamma function can be extended to all real and complex values (except the negative integers and zero) by using the unique analytic continuation

Analytic continuation

of f.

Main definition

The notation

is due to Legendre

Adrien-Marie Legendre

Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...

. If the real part of the complex number z is positive (Re(z) > 0), then the integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

converges absolutely

Absolute convergence

In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...

. Using integration by parts

Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...

, we see that the gamma function satisfies the functional equation

Functional equation

In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...

Combining this with

, we get:

for all positive integers n.

The identity Γ(z) = Γ(z+1) / z can be used (or, yielding the same result, analytic continuation

Analytic continuation

can be used) to extend the integral formulation for Γ(z) to a meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

defined for all complex numbers z, except z = −n for integers n ≥ 0, where the function has simple poles with residue

Residue (complex analysis)

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...

(−1)ⁿ/n!.

It is this extended version that is commonly referred to as the gamma function.

Alternative definitions

The following infinite product definitions for the gamma function, due to Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

and Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....

respectively, are valid for all complex numbers z, except the non-positive integers:

where

is the Euler–Mascheroni constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

.
It is straightforward to show that the Euler definition satisfies the functional equation

Functional equation

(1) above.

A somewhat curious parametrization of the gamma function is given in terms of generalized Laguerre polynomials,

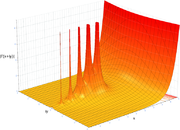
which converges for Re(z) < 1/2.

The gamma function in the complex plane

The behavior of

for an increasing positive variable is simple: it grows quickly — faster than an exponential function. Asymptotically as

, the magnitude of the gamma function is given by Stirling's formula

where the symbol ~ means that the quotient of both sides converges to 1.

The behavior for nonpositive z is more intricate. Euler's integral does not converge for z ≤ 0, but the function it defines in the positive complex half-plane has a unique analytic continuation

Analytic continuation

to the negative half-plane. One way to find that analytic continuation is to use Euler's integral for positive arguments and extend the domain to negative numbers by repeated application of the recurrence formula,

choosing n such that z + n is positive. The product in the denominator is zero when z equals any of the integers 0, −1, −2,... . Thus, the gamma function must be undefined at those points due to division by zero; it is a meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

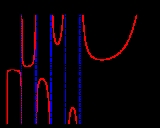
with poles at the nonpositive integers. The following image shows the graph of the gamma function along the real line:
The gamma function is nonzero everywhere along the real line, although it comes arbitrarily close as

. There is in fact no complex number z for which

, and hence the reciprocal gamma function

is an entire function

Entire function

In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...

, with zeros at z = 0, −1, −2,.... We see that the gamma function has a local minimum at

where it attains the value

. The gamma function must alternate sign between the poles because the product in the forward recurrence contains an odd number of negative factors if the number of poles between

and

is odd, and an even number if the number of poles is even.

Plotting the gamma function in the complex plane yields:

General

Other important functional equations for the gamma function are Euler's reflection formula

Reflection formula

In mathematics, a reflection formula or reflection relation for a function f is a relationship between f and f...

and the duplication formula

The duplication formula is a special case of the multiplication theorem

Multiplication theorem

In mathematics, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function. For the explicit case of the gamma function, the identity is a product of values; thus the name...

A simple but useful property, which can be seen from the limit definition, is:

Perhaps the best-known value of the gamma function at a non-integer argument is

which can be found by setting z = 1/2 in the reflection or duplication formulas, by using the relation to the beta function given below with x = y = 1/2, or simply by making the substitution u = √t in the integral definition of the gamma function, resulting in a Gaussian integral

Gaussian integral

The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...

. In general, for non-negative integer values of n we have:

where n!! denotes the double factorial and, when n = 0, (-1)!! = 1. See Particular values of the gamma function

Particular values of the Gamma function

The Gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer and half-integer arguments, but no simple expressions are known for the values at rational points in general...

for calculated values.

It might be tempting to generalize the result that

by looking for a formula for other individual values

where

is rational. However, these numbers are not known to be expressible by themselves in terms of elementary functions. It has been proved that

is a transcendental number

Transcendental number

In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...

and algebraically independent

Algebraic independence

In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K...

for any integer

and each of the fractions

= 1/6, 1/4, 1/3, 2/3, 3/4, and 5/6. In general, when computing values of the gamma function, we must settle for numerical approximations.

The derivatives of the gamma function are described in terms of the polygamma function. For example:

For positive integer m the derivative of gamma function can be calculated as follows (here γ is the Euler–Mascheroni constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

The n-th derivative of the gamma function is:

The gamma function has simple poles at z = −n = 0, −1, −2, −3, ... . The residue

Residue (complex analysis)

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...

there is

Moreover, the gamma function has the following Laurent expansion

Laurent series

In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...

in 0

valid for |z|<1. In particular

The Bohr–Mollerup theorem states that among all functions extending the factorial functions to the positive real numbers, only the gamma function is log-convex, that is, its natural logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

is convex

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

Pi function

An alternative notation which was originally introduced by Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

and which was sometimes used is the Pi function, which in terms of the gamma function is

so that

for every non-negative integer n.

Using the Pi function the reflection formula takes on the form

where sinc is the normalized sinc function, while the multiplication theorem takes on the form

We also sometimes find

which is an entire function

Entire function

In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...

, defined for every complex number. That π(z) is entire entails it has no poles, so Γ(z) has no zeros

Zero (complex analysis)

In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...

Relation to other functions

In the first integral above, which defines the gamma function, the limits of integration are fixed. The upper and lower incomplete gamma functions
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...

are the functions obtained by allowing the lower or upper (respectively) limit of integration to vary.
The gamma function is related to the Beta function by the formula

The derivative of the logarithm of the gamma function is called the digamma function; higher derivatives are the polygamma functions.
The analog of the gamma function over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...

or a finite ring
Finite ring
In mathematics, more specifically abstract algebra, a finite ring is a ring that has a finite number of elements....

is the Gaussian sums, a type of exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...

.
The reciprocal gamma function is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...

and has been studied as a specific topic.
The gamma function also shows up in an important relation with the Riemann zeta function, ζ(z).

And also in the following elegant formula:

which is valid only for Re(z) > 1.

The logarithm of the gamma function satisfies the following formula due to Lerch:

where

is the Hurwitz zeta function,

is the Riemann zeta function and the prime (') denotes differentiation in the first variable.

The gamma function is intimately related to the stretched exponential function. For instance, the moments of that function are

Particular values

Main article: Particular values of the gamma function
Particular values of the Gamma function
The Gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer and half-integer arguments, but no simple expressions are known for the values at rational points in general...

Some particular values of the gamma function are:

Approximations

Complex values of the gamma function can be computed numerically with arbitrary precision using Stirling's approximation

Stirling's approximation

In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...

or the Lanczos approximation.

The gamma function can be computed to fixed precision for Re(z) ∈ [1, 2] by applying integration by parts

Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...

to Euler's integral. For any positive number x the gamma function can be written

When Re(z) ∈ [1, 2] and x ≥ 1, the absolute value of the last integral is smaller than (x + 1) e^−x. By choosing x large enough, this last expression can be made smaller than 2^−N for any desired value N. Thus, the gamma function can be evaluated to N bits of precision with the above series. When z is rational, the computation can be performed with binary splitting

Binary splitting

In mathematics, binary splitting is a technique for speeding up numerical evaluation of many types of series with rational terms. In particular, it can be used to evaluate hypergeometric series at rational points...

in time O((log N)² M(N)) where M(N) is the time needed to multiply two N-bit numbers.

For arguments that are integer multiples of 1/24 the gamma function can also be evaluated quickly using arithmetic-geometric mean iterations (see particular values of the gamma function

Particular values of the Gamma function

).

Because the Gamma and factorial functions grow so rapidly for moderately-large arguments, many computing environments include a function that returns the natural logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

of the gamma function (often given the name lngamma in programming environments or gammaln in spreadsheets); this grows much more slowly, and for combinatorial calculations allows adding and subtracting logs instead of multiplying and dividing very large values. The digamma function, which is the derivative of this function, is also commonly seen.
In the context of technical and physical applications, e.g. with wave propagation, the functional equation

is often used since it allows one to determine function values in one strip of width 1 in z from the neighbouring strip. In particular, starting with a good approximation for a z with large real part one may go step by step down to the desired z.
Following an indication of Carl Friedrich Gauss

Carl Friedrich Gauss

, Rocktaeschel (1922) proposed for lngamma an approximation for large Re(z):

This can be used to accurately approximate

for z with a smaller Re(z) via (P.E.Böhmer, 1939)

A more accurate approximation can be obtained by using more terms from the asymptotic expansions of

and

, which are based on Stirling's approximation.

An asymptotic approximation of the gamma function is

Applications

Opening a random page in an advanced table of formulas, one may be as likely to spot the gamma function as a trigonometric function. One author describes the gamma function as "Arguably, the most common special function, or the least 'special' of them. The other transcendental functions listed below are called 'special' because you could conceivably avoid some of them by staying away from many specialized mathematical topics. On the other hand, the gamma function

is most difficult to avoid."

Integration problems

The gamma function finds application in such diverse areas as quantum physics, astrophysics

Astrophysics

Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...

and fluid dynamics

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

. The gamma distribution, which is formulated in terms of the gamma function, is used in statistics

Statistics

to model a wide range of processes; for example, the time between occurrences of earthquakes.

The primary reason for the gamma function's usefulness in such contexts is the prevalence of expressions of the type

which describe processes that decay exponentially in time or space. Integrals of such expressions can occasionally be solved in terms of the gamma function when no elementary solution exists. For example, if

is a power function and

is a linear function, a simple change of variables gives the evaluation

The fact that the integration is performed along the entire positive real line might signify that the gamma function describes the cumulation of a time-dependent process that continues indefinitely, or the value might be the total of a distribution in an infinite space.

It is of course frequently useful to take limits of integration other than 0 and

to describe the cumulation of a finite process, in which case the ordinary gamma function is no longer a solution; the solution is then called an incomplete gamma function

Incomplete gamma function

In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...

. (The ordinary gamma function, obtained by integrating across the entire positive real line, is sometimes called the complete gamma function for contrast).

An important category of exponentially decaying functions is that of Gaussian functions

and integrals thereof, such as the error function

Error function

In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...

. There are many interrelations between these functions and the gamma function; notably, the square root of

we obtained by evaluating

is the "same" as that found in the normalizing factor of the error function and the normal distribution.

The integrals we have discussed so far involve transcendental functions, but the gamma function also arises from integrals of purely algebraic functions. In particular, the arc length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

s of ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

s and of the lemniscate

Lemniscate

In algebraic geometry, a lemniscate refers to any of several figure-eight or ∞ shaped curves. It may refer to:*The lemniscate of Bernoulli, often simply called the lemniscate, the locus of points whose product of distances from two foci equals the square of half the interfocal distance*The...

, which are curves defined by algebraic equations, are given by elliptic integral

Elliptic integral

In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...

s that in special cases can be evaluated in terms of the gamma function. The gamma function can also be used to calculate "volume" and "area" of

-dimensional hypersphere

Hypersphere

In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...

s.

Another important special case is that of the beta function

Calculating products

The gamma function's ability to and generalize factorial products immediately leads to applications in many areas of mathematics; in combinatorics

Combinatorics

, and by extension in areas such as probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

and the calculation of power series. Many expressions involving products of successive integers can be written as some combination of factorials, the most important example perhaps being that of the binomial coefficient

Binomial coefficient

In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

The example of binomial coefficients motivates why the properties of the gamma function when extended to negative numbers are natural. A binomial coefficient gives the number of ways to choose

elements from a set of

elements; if

, there are of course no ways. If

is the factorial of a negative integer and hence infinite if we use the gamma function definition of factorials — dividing by infinity gives the expected value of 0.

We can replace the factorial by a gamma function to extend any such formula to the complex numbers. Generally, this works for any product wherein each factor is a rational function

Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

of the index variable, by factoring the rational function into linear expressions. If

and

are monic polynomials of degree

and

with respective roots

and

, we have

If we have a way to calculate the gamma function numerically, it is a breeze to calculate numerical values of such products. The number of gamma functions in the right-hand side depends only on the degree of the polynomials, so it does not matter whether

equals 5 or

. Moreover, due to the poles of the gamma function, the equation also holds (in the sense of taking limits) when the left-hand product contain zeros or poles.

By taking limits, certain rational products with infinitely many factors can be evaluated in terms of the gamma function as well. Due to the Weierstrass factorization theorem

Weierstrass factorization theorem

In mathematics, the Weierstrass factorization theorem in complex analysis, named after Karl Weierstrass, asserts that entire functions can be represented by a product involving their zeroes...

, analytic functions can be written as infinite products, and these can sometimes be represented as finite products or quotients of the gamma function. We have already seen one striking example: the reflection formula essentially represents the sine function as the product of two gamma functions. Starting from this formula, the exponential function as well as all the trigonometric and hyperbolic functions can be expressed in terms of the gamma function.

More functions yet, including the hypergeometric function and special cases thereof, can be represented by means of complex contour integrals of products and quotients of the gamma function, called Mellin-Barnes integrals.

Analytic number theory

An elegant and deep application of the gamma function is in the study of the Riemann zeta function. A fundamental property of the Riemann zeta function is its functional equation

Functional equation

Among other things, this provides an explicit form for the analytic continuation

Analytic continuation

of the zeta function to a meromorphic function in the complex plane and leads to an immediate proof that the zeta function has infinitely many so-called "trivial" zeros on the real line. Borwein et al. call this formula "one of the most beautiful findings in mathematics". Another champion for that title might be

Both formulas were derived by Bernhard Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

in his seminal 1859 paper "Über die Anzahl der Primzahlen unter einer gegebenen Grösse" ("On the Number of Prime Numbers less than a Given Quantity"), one of the milestones in the development of analytic number theory

Analytic number theory

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...

— the branch of mathematics that studies prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

s using the tools of mathematical analysis. Factorial numbers, considered as discrete objects, are an important concept in classical number theory because they contain many prime factors, but Riemann found a use for their continuous extension that arguably turned out to be even more important.

History

The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, notably documented by Philip J. Davis

Philip J. Davis

Philip J. Davis is an American applied mathematician.Davis was born in Lawrence, Massachusetts. He is known for his work in numerical analysis and approximation theory, as well as his investigations in the history and philosophy of mathematics...

in an article that won him the 1963 Chauvenet Prize

Chauvenet Prize

The Chauvenet Prize is the highest award for mathematical expository writing. It consists of a prize of $1,000 and a certificate, and is awarded yearly by the Mathematical Association of America in recognition of an outstanding expository article on a mathematical topic. The prize is named in...

, reflects many of the major developments within mathematics since the 18th century. In the words of Davis, "each generation has found something of interest to say about the gamma function. Perhaps the next generation will also."

18th century: Euler and Stirling

The problem of extending the factorial to non-integer arguments was apparently first considered by Daniel Bernoulli

Daniel Bernoulli

Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...

and Christian Goldbach

Christian Goldbach

Christian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...

in the 1720s, and was solved at the end of the same decade by Leonhard Euler

Leonhard Euler

. Euler gave two different definitions: the first was not his integral but an infinite product,

of which he informed Goldbach in a letter dated October 13, 1729. He wrote to Goldbach again on January 8, 1730, to announce his discovery of the integral representation

which is valid for n > 0. By the change of variables t = −log s, this becomes the familiar Euler integral. Euler published his results in the paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("On transcendental progressions, that is, those whose general terms cannot be given algebraically"), submitted to the St. Petersburg Academy on November 28, 1729. Euler further discovered some of the gamma function's important functional properties, including the reflection formula.

James Stirling

James Stirling (mathematician)

James Stirling was a Scottish mathematician. The Stirling numbers and Stirling's approximation are named after him.-Biography:...

, a contemporary of Euler, also attempted to find a continuous expression for the factorial and came up with what is now known as Stirling's formula. Although Stirling's formula gives a good estimate of

, also for non-integers, it does not provide the exact value. Extensions of his formula that correct the error were given by Stirling himself and by Jacques Philippe Marie Binet

Jacques Philippe Marie Binet

Jacques Philippe Marie Binet was a French mathematician, physicist and astronomer born in Rennes; he died in Paris, France, in 1856. He made significant contributions to number theory, and the mathematical foundations of matrix algebra which would later lead to important contributions by Cayley...

19th century: Gauss, Weierstrass and Legendre

Carl Friedrich Gauss

rewrote Euler's product as

and used this formula to discover new properties of the gamma function. Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex number, as instead Gauss first did. Gauss also proved the multiplication theorem

Multiplication theorem

of the gamma function and investigated the connection between the gamma function and elliptic integral

Elliptic integral

In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...

s.

Karl Weierstrass

Karl Weierstrass

further established the role of the gamma function in complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, starting from yet another product representation,

where γ is the Euler–Mascheroni constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

. Weierstrass originally wrote his product as one for

, in which case it is taken over the function's zeros rather than its poles. Inspired by this result, he proved what is known as the Weierstrass factorization theorem

Weierstrass factorization theorem

In mathematics, the Weierstrass factorization theorem in complex analysis, named after Karl Weierstrass, asserts that entire functions can be represented by a product involving their zeroes...

—that any entire function can be written as a product over its zeros in the complex plane; a generalization of the fundamental theorem of algebra

Fundamental theorem of algebra

The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...

.

The name gamma function and the symbol

were introduced by Adrien-Marie Legendre

Adrien-Marie Legendre

Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...

around 1811; Legendre also rewrote Euler's integral definition in its modern form. Although the symbol is an upper-case Greek gamma, there is no accepted standard for whether the function name should be written "gamma function" or "Gamma function" (some authors simply write "

-function"). The alternative "Pi function" notation

due to Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works.

It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to

instead of simply using "

". Consider that the notation for exponents,

, has been generalized from integers to complex numbers

without any change. Legendre's motivation for the normalization
does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician Cornelius Lanczos

Cornelius Lanczos

Cornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....

, for example, called it "void of any rationality" and would instead use

). Legendre's normalization does simplify a few formulas, but complicates most others.

19th-20th centuries: characterizing the gamma function

It is somewhat problematic that a large number of definitions have been given for the gamma function. Although they describe the same function, it is not entirely straightforward to prove the equivalence. Stirling never proved that his extended formula corresponds exactly to Euler's gamma function; a proof was first given by Charles Hermite

Charles Hermite

Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....

in 1900. Instead of finding a specialized proof for each formula, it would be desirable to have a general method of identifying the gamma function.

One way to prove would be to find a differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

that characterizes the gamma function. Most special functions in applied mathematics arise as solutions to differential equations, whose solutions are unique. However, the gamma function does not appear to satisfy any simple differential equation. Otto Hölder

Otto Hölder

Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...

proved in 1887 that the gamma function at least does not satisfy any algebraic differential equation

Algebraic differential equation

In mathematics, an algebraic differential equation is a differential equation that can be expressed by means of differential algebra. There are several such notions, according to the concept of differential algebra used....

by showing that a solution to such an equation could not satisfy the gamma function's recurrence formula. This result is known as Hölder's theorem

Hölder's theorem

In mathematics, Hölder's theorem states that the gamma function does not satisfy any algebraic differential equation whose coefficients are rational functions. The result was first proved by Otto Hölder in 1887; several alternative proofs have subsequently been found.The theorem also generalizes to...

.

A definite and generally applicable characterization of the gamma function was not given until 1922. Harald Bohr

Harald Bohr

Harald August Bohr was a Danish mathematician and football player. After receiving his doctorate in 1910, Bohr became an eminent mathematician, founding the field of almost periodic functions. His brother was the Nobel Prize-winning physicist Niels Bohr...

and Johannes Mollerup then proved what is known as the Bohr–Mollerup theorem: that the gamma function is the unique solution to the factorial recurrence relation that is positive and logarithmically convex for positive z and whose value at 1 is 1 (a function is logarithmically convex if its logarithm is convex).

The Bohr–Mollerup theorem is useful because it is relatively easy to prove logarithmic convexity for any of the different formulas used to define the gamma function. Taking things further, instead of defining the gamma function by any particular formula, we can choose the conditions of the Bohr–Mollerup theorem as the definition, and then pick any formula we like that satisfies the conditions as a starting point for studying the gamma function. This approach was used by the Bourbaki group.

Reference tables and software

Although the gamma function can be calculated virtually as easily as any mathematically simpler function with a modern computer—even with a programmable pocket calculator—this was of course not always the case. Until the mid-20th century, mathematicians relied on hand-made tables; in the case of the gamma function, notably a table computed by Gauss in 1813 and one computed by Legendre in 1825.

Tables of complex values of the gamma function, as well as hand-drawn graphs, were given in Tables of Higher Functions by Jahnke and Emde, first published in Germany in 1909. According to Michael Berry, "the publication in J&E of a three-dimensional graph showing the poles of the gamma function in the complex plane acquired an almost iconic status."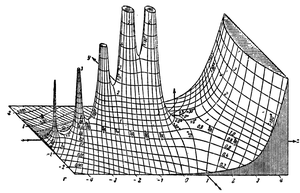

There was in fact little practical need for anything but real values of the gamma function until the 1930s, when applications for the complex gamma function were discovered in theoretical physics. As electronic computers became available for the production of tables in the 1950s, several extensive tables for the complex gamma function were published to meet the demand, including a table accurate to 12 decimal places from the U.S. National Bureau of Standards.

Abramowitz and Stegun
Abramowitz and Stegun
Abramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...

became the standard reference for this and many other special functions after its publication in 1964.

Double-precision floating-point implementations of the gamma function and its logarithm are now available in most scientific computing software and special functions libraries, for example Matlab

MATLAB

MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...

, GNU Octave

GNU Octave

GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...

, and the GNU Scientific Library

GNU Scientific Library

In computing, the GNU Scientific Library is a software library written in the C programming language for numerical calculations in applied mathematics and science...

. The gamma function was also added to the C

C (programming language)

C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....

standard library (math.h). Arbitrary-precision implementations are available in most computer algebra system

Computer algebra system

A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...

s, such as Mathematica

Mathematica

Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...

and Maple

Maple (software)

Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....

. PARI/GP

PARI/GP

PARI/GP is a computer algebra system with the main aim of facilitating number theory computations. It is free software; versions 2.1.0 and higher are distributed under the GNU General Public License...

, MPFR

MPFR

GNU MPFR is a portable C library for arbitrary-precision binary floating-point computation with correct rounding, based on GNU Multi-Precision Library. The computation is both efficient and has a well-defined semantics. It copies the ideas from the ANSI/IEEE-754 standard for fixed-precision...

and MPFUN contain free arbitrary-precision implementations.

External links

Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
C++ reference for std::tgamma
Examples of problems involving the gamma function can be found at Exampleproblems.com.
Wolfram gamma function evaluator (arbitrary precision)
Volume of n-Spheres and the Gamma Function at MathPages
"Elementary Proofs and Derivations"
"Selected Transformations, Identities, and Special Values for the Gamma Function"

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.