Rational function
Encyclopedia
In mathematics
, a rational function is any function
which can be written as the ratio
of two polynomial functions. Neither the coefficient
s of the polynomials nor the values
taken by the function are necessarily rational
.
,
, a function is called a rational function if and only if it can be written in the form
where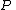
and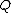 
are polynomial functions in 
and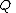 
is not the zero polynomial. The domain
of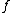
is the set of all points 
for which the denominator 
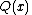is not zero, where one assumes that the fraction is written in its lower degree terms, that is, 
and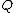 
have several factors of the positive degree.
Every polynomial function is a rational function with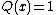
. A function that cannot be written in this form (for example, 
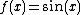) is not a rational function (but the adjective "irrational" is not generally used for functions, but only for numbers).
An expression of the form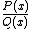
is called a rational expression. The 
need not be a variable. In abstract algebra
the
is called an indeterminate
.
A rational equation is an equation in which two rational expressions are set equal to each other. These expressions obey the same rules as fractions
. The equations can be solved by cross-multiplying. Division by zero is undefined, so that a solution causing formal division by zero is rejected.
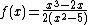is not defined at 
.
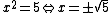The rational function
is defined for all real number
s, but not for all complex number
s, since if x were the square root of
(i.e. the imaginary unit
) or its negative, then formal evaluation would lead to division by zero: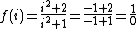
, which is undefined.
The rational function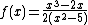
, as x approaches infinity, is asymptotic to 
.
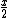A constant function
such as f(x) = π is a rational function since constants are polynomials. Note that the function itself is rational, even though f(x) is irrational for all x.
The rational function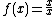
is equal to 1 for all x except 0, where there is a removable discontinuity.
The sum, product, or quotient (excepting division by the zero polynomial) of two rational functions is itself a rational function: however, the process of reduction to standard form may inadvertently result in the removing of such discontinuities unless care is taken.
of any rational function satisfy a linear recurrence relation
, which can be found by setting the rational function equal to its Taylor series and collecting like terms.
For example,
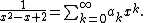
Multiplying through by the denominator and distributing,
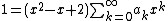
After adjusting the indices of the sums to get the same powers of x, we get
Combining like terms gives
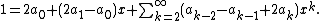
Since this holds true for all x in the radius of convergence of the original Taylor series, we can compute as follows. Since the constant term
on the left must equal the constant term on the right it follows that
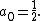
Then, since there are no powers of x on the left, all of the coefficient
s on the right must be zero, from which it follows that
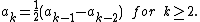
Conversely, any sequence that satisfies a linear recurrence determines a rational function when used as the coefficients of a Taylor series. This is useful in solving such recurrences, since by using partial fraction decomposition
we can write any rational function as a sum of factors of the form 1 / (ax + b) and expand these as geometric series, giving an explicit formula for the Taylor coefficients; this is the method of generating functions.
In abstract algebra
the concept of a polynomial is extended to include formal expressions in which the coefficients of the polynomial can be taken from any field
. In this setting given a field F and some indeterminate X, a rational expression is any element of the field of fractions
of the polynomial ring
F[X]. Any rational expression can be written as the quotient of two polynomials P/Q with Q ≠ 0, although this representation isn't unique. P/Q is equivalent to R/S, for polynomials P, Q, R, and S, when PS = QR. However since F[X] is a unique factorization domain
, there is a unique representation
for any rational expression P/Q with P and Q polynomials of lowest degree and Q chosen to be monic. This is similar to how a fraction
of integers can always be written uniquely in lowest terms by canceling out common factors.
The field of rational expressions is denoted F(X). This field is said to be generated (as a field) over F by (a transcendental element) X, because F(X) does not contain any proper subfield containing both F and the element X.
, a rational function
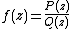
is the ratio of two polynomials with complex coefficients, where Q is not the zero polynomial and P and Q have no common factor (this avoids f taking the indeterminate value 0/0). The domain and range of f are usually taken to be the Riemann sphere
, which avoids any need for special treatment at the poles of the function (where Q(z) is 0).
The degree of a rational function is the maximum of the degrees
of its constituent polynomials P and Q. If the degree of f is d, then the equation
has d distinct solutions in z except for certain values of w, called critical values, where two or more solutions coincide. The function f can therefore be thought of as a d-fold covering
of the w-sphere by the z-sphere.
Rational functions with degree 1 are called Möbius transformations and form the automorphism
s group
of the Riemann sphere
. Rational functions are representative examples of meromorphic function
s.
An extended version of the abstract idea of rational function is used in algebraic geometry. There the function field of an algebraic variety
V is formed as the field of fractions of the coordinate ring of V (more accurately said, of a Zariski-dense affine open set in V). Its elements f are considered as regular functions in the sense of algebraic geometry on non-empty open sets U, and also may be seen as morphisms to the projective line
.
, especially in the construction of field extension
s. They also provide an example of a nonarchimedean field (see Archimedean property
).
Rational functions are used in numerical analysis
for interpolation
and approximation
of functions, for example the Padé approximations introduced by Henri Padé
. Approximations in terms of rational functions are well suited for computer algebra system
s and other numerical software. Like polynomials, they can be evaluated straightforwardly, and at the same time they express more diverse behavior than polynomials.
Rational functions are used to approximate or model more complex equations in science and engineering including (i) fields and forces in physics, (ii) spectroscopy in analytical chemistry, (iii) enzyme kinetics in biochemistry, (iv) electronic circuitry, (v) aerodynamics, (vi) medicine concentrations in vivo, (vii) wave functions for atoms and molecules,
(viii) optics and photography to improve image resolution, and (ix) acoustics and sound.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a rational function is any function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which can be written as the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of two polynomial functions. Neither the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of the polynomials nor the values
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
taken by the function are necessarily rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
.
Definitions
In the case of one variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
,
, a function is called a rational function if and only if it can be written in the formwhere
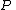and 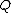are polynomial functions in and 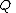is not the zero polynomial. The domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of
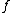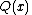is the set of all points for which the denominator is not zero, where one assumes that the fraction is written in its lower degree terms, that is, and 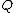have several factors of the positive degree.Every polynomial function is a rational function with
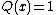. A function that cannot be written in this form (for example, 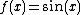) is not a rational function (but the adjective "irrational" is not generally used for functions, but only for numbers).An expression of the form
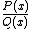is called a rational expression. The need not be a variable. In abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
the
is called an indeterminateIndeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
.
A rational equation is an equation in which two rational expressions are set equal to each other. These expressions obey the same rules as fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
. The equations can be solved by cross-multiplying. Division by zero is undefined, so that a solution causing formal division by zero is rejected.
Examples
The rational function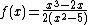 is not defined at 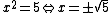.The rational function
is defined for all real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, but not for all complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, since if x were the square root of
(i.e. the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
) or its negative, then formal evaluation would lead to division by zero:
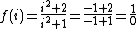, which is undefined.The rational function
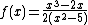, as x approaches infinity, is asymptotic to 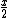.A constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
such as f(x) = π is a rational function since constants are polynomials. Note that the function itself is rational, even though f(x) is irrational for all x.
The rational function
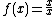is equal to 1 for all x except 0, where there is a removable discontinuity.The sum, product, or quotient (excepting division by the zero polynomial) of two rational functions is itself a rational function: however, the process of reduction to standard form may inadvertently result in the removing of such discontinuities unless care is taken.
Taylor series
The coefficients of a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of any rational function satisfy a linear recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
, which can be found by setting the rational function equal to its Taylor series and collecting like terms.
For example,
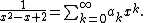
Multiplying through by the denominator and distributing,
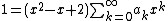
After adjusting the indices of the sums to get the same powers of x, we get
Combining like terms gives
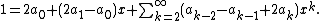
Since this holds true for all x in the radius of convergence of the original Taylor series, we can compute as follows. Since the constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
on the left must equal the constant term on the right it follows that
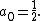
Then, since there are no powers of x on the left, all of the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s on the right must be zero, from which it follows that
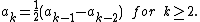
Conversely, any sequence that satisfies a linear recurrence determines a rational function when used as the coefficients of a Taylor series. This is useful in solving such recurrences, since by using partial fraction decomposition
Partial fraction
In algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
we can write any rational function as a sum of factors of the form 1 / (ax + b) and expand these as geometric series, giving an explicit formula for the Taylor coefficients; this is the method of generating functions.
Abstract algebra and geometric notion
In abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
the concept of a polynomial is extended to include formal expressions in which the coefficients of the polynomial can be taken from any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. In this setting given a field F and some indeterminate X, a rational expression is any element of the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
F[X]. Any rational expression can be written as the quotient of two polynomials P/Q with Q ≠ 0, although this representation isn't unique. P/Q is equivalent to R/S, for polynomials P, Q, R, and S, when PS = QR. However since F[X] is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
, there is a unique representation
Irreducible fraction
An irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
for any rational expression P/Q with P and Q polynomials of lowest degree and Q chosen to be monic. This is similar to how a fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
of integers can always be written uniquely in lowest terms by canceling out common factors.
The field of rational expressions is denoted F(X). This field is said to be generated (as a field) over F by (a transcendental element) X, because F(X) does not contain any proper subfield containing both F and the element X.
Complex rational functions
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a rational function
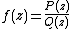
is the ratio of two polynomials with complex coefficients, where Q is not the zero polynomial and P and Q have no common factor (this avoids f taking the indeterminate value 0/0). The domain and range of f are usually taken to be the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, which avoids any need for special treatment at the poles of the function (where Q(z) is 0).
The degree of a rational function is the maximum of the degrees
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
of its constituent polynomials P and Q. If the degree of f is d, then the equation
has d distinct solutions in z except for certain values of w, called critical values, where two or more solutions coincide. The function f can therefore be thought of as a d-fold covering
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
of the w-sphere by the z-sphere.
Rational functions with degree 1 are called Möbius transformations and form the automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Rational functions are representative examples of meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s.
Notion of a rational function on an algebraic variety
Like polynomials, rational expressions can also be generalized to n indeterminates X1,..., Xn, by taking the field of fractions of F[X1,..., Xn], which is denoted by F(X1,..., Xn).An extended version of the abstract idea of rational function is used in algebraic geometry. There the function field of an algebraic variety
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
V is formed as the field of fractions of the coordinate ring of V (more accurately said, of a Zariski-dense affine open set in V). Its elements f are considered as regular functions in the sense of algebraic geometry on non-empty open sets U, and also may be seen as morphisms to the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
.
Applications
These objects are first encountered in school algebra. In more advanced mathematics they play an important role in ring theoryRing theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, especially in the construction of field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s. They also provide an example of a nonarchimedean field (see Archimedean property
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
).
Rational functions are used in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
for interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
and approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
of functions, for example the Padé approximations introduced by Henri Padé
Henri Padé
Henri Eugène Padé was a French mathematician, who is now remembered mainly for his development of approximation techniques for functions using rational functions.He was educated at École Normale Supérieure in Paris...
. Approximations in terms of rational functions are well suited for computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s and other numerical software. Like polynomials, they can be evaluated straightforwardly, and at the same time they express more diverse behavior than polynomials.
Rational functions are used to approximate or model more complex equations in science and engineering including (i) fields and forces in physics, (ii) spectroscopy in analytical chemistry, (iii) enzyme kinetics in biochemistry, (iv) electronic circuitry, (v) aerodynamics, (vi) medicine concentrations in vivo, (vii) wave functions for atoms and molecules,
(viii) optics and photography to improve image resolution, and (ix) acoustics and sound.
See also
- Partial fraction decomposition
- Partial fractions in integrationPartial fractions in integrationIn integral calculus, partial fraction expansions provide an approach to integrating a general rational function. Any rational function of a real variable can be written as the sum of a polynomial function and a finite number of algebraic fractions...
- Function field of an algebraic varietyFunction field of an algebraic varietyIn algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...