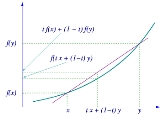
Convex function
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a real-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
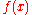defined on an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
is called convex (or convex downward or concave upward) if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph
Epigraph (mathematics)
In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....
(the set of points on or above the graph of the function) is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
.
Unanswered Questions
