Number theory
Encyclopedia
Number theory is a branch of pure mathematics
devoted primarily to the study of the integers. Number theorists study prime numbers (which, when multiplied, give all the integers) as well
as the properties of objects made out of integers (such as rational numbers) or defined as generalizations of the integers (such as, for example, algebraic integers).
Integers can be considered either in themselves or as solutions to equations
(diophantine geometry
). Questions in number theory are often best understood through
the study of analytical
objects (e.g., the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory
). One may also study real numbers in relation to rational numbers, e.g., as approximated by the latter (diophantine approximation
).
The older term for number theory is arithmetic; by the early twentieth century, it had been superseded by "number theory". (The word "arithmetic" is used by the general public to mean "elementary calculations"; it has also acquired other meanings in mathematical logic
, as in Peano arithmetic, and computer science
, as in floating point arithmetic
.) The use of the term arithmetic for number theory regained some ground in the second half of the 20th century, arguably in part due to French influence. In particular, arithmetical is preferred as an adjective to number-theoretic.
find of an arithmetical nature is a fragment of a table: the broken clay tablet
Plimpton 322
(Larsa, Mesopotamia, ca. 1800 BCE) contains a list of "Pythagorean triples", i.e., integers
such that 
.
The triples are too many and too large to have been obtained by brute force.
The heading over the first column reads: "The takiltum of the diagonal which has been substracted such that the width..."
The table's outlay suggests that it was constructed by means of what amounts, in modern language, to the identity
which is implicit in routine Old Babylonian exercises. If some other method was used, the triples were first
constructed and then reordered by
, presumably for actual use as a "table",
i.e., with a view to applications.
We do not know what these applications may have been, or whether there could have been any; Babylonian astronomy, for example, truly flowered only later. It has been suggested instead that the table was a source of numerical examples for school problems.
While Babylonian number theory – or what survives of Babylonian mathematics that can be called thus – consists of this single, striking fragment,
Babylonian algebra (in the
secondary-school sense of "algebra") was exceptionally well developed. Late Neoplatonic sources state that Pythagoras
learned mathematics from the Babylonians. (Much earlier sources state that Thales
and Pythagoras
travelled and studied in Egypt
.)
Euclid IX 21—34
is very probably Pythagorean; it is very simple material
("odd times even is odd", "if an odd number measures [= divides] an even number, then it also measures [= divides] half of it"), but it is all that is needed to prove that
is irrational
. (Pythagoraean mystics gave great importance to the odd and the even.)
The discovery that
is irrational is credited
to the early Pythagoreans (pre-Theodorus
). By revealing (in modern
terms) that numbers could be irrational, this discovery seems to have
provoked the first foundational crisis in mathematical history; its proof or its divulgation
are sometimes credited to Hippasus, who was expelled or split from
the Pythagorean sect. It is only here that we can start to speak of a clear, conscious division between
numbers (integers and the rationals – the subjects of arithmetic) and lengths (real numbers, whether rational or not).
The Pythagorean tradition spoke also of so-called polygonal
or figured numbers. While square numbers, cubic numbers, etc., are seen now as more natural than triangular numbers, square numbers, pentagonal numbers, etc., the study of the sums
of triangular and pentagonal numbers would prove fruitful in the early modern period (17th to early 19th century).
We know of no clearly arithmetical material in ancient Egyptian
or Vedic
sources, though there is some algebra in both. The Chinese remainder theorem
appears as an exercise in Sun Zi
's Suan Ching (also known as Sun Tzu's Mathematical Classic; 3rd, 4th or 5th century CE.). (There is one important step glossed over in Sun Zi's solution: it is the problem that was later solved by Āryabhaṭa
's kuṭṭaka – see below.)
There is also some numerical mysticism in Chinese mathematics, but, unlike that of the Pythagoreans, it seems to have
led nowhere. Like the Pythagoreans' perfect numbers, magic squares have passed from superstition into recreation.
means, by and large, Plato and Euclid, respectively.
Plato
had a keen interest in mathematics, and distinguished clearly between arithmetic and calculation. (By arithmetic he meant, in part, theorising on number, rather than what arithmetic or number theory have come to mean.) It is through one of Plato's dialogues—namely,
Theaetetus
– that we know that Theodorus
had proven that
are irrational. Theaetetus was, like Plato, a disciple of Theodorus's; he worked on distinguishing different kind of inconmensurables, and was thus arguably a pioneer in the study of number systems. (Book X of Euclid's Elements
is described by Pappus
as being largely based on Theaetetus's work.)
Euclid
devoted part of his Elements to prime numbers and divisibility, topics that belong unambiguously to number theory and are basic thereto (Books VII to IX of Euclid's Elements
).
In particular, he gave an algorithm for computing the greatest common divisor of two numbers
(the Euclidean algorithm
; Elements, Prop. VII.2) and the first known proof of the infinitude of primes (Elements, Prop. IX.20).
In 1773, Lessing
published an epigram
he had found in a manuscript during his work as a librarian; it claimed to be a letter sent by Archimedes
to Eratosthenes
. The epigram proposed what has become known as
Archimedes' cattle problem
; its solution (absent from the manuscript) requires solving an indeterminate quadratic equation (which reduces to what would later be misnamed Pell's equation
). As far as we know, such equations were first successfully treated by the Indian school. It is not known whether Archimedes himself had a method of solution.
Very little is known about Diophantus of Alexandria; he probably lived in the third century CE, that is, about five hundred years after Euclid. Six out of the thirteen books
of Diophantus's Arithmetica
survive in the original Greek; four more books survive in an Arabic translation. The Arithmetica is a collection of worked-out problems where the task is invariably to find rational solutions to a system of polynomial equations, usually of the form
or 
. Thus, nowadays, we speak of Diophantine equations when we speak of polynomial equations to which rational or integer solutions must be found.
One may say that Diophantus was studying rational points—i.e., points whose coordinates are rational—on curve
s and varieties
; however, unlike the Greeks of the Classical period, who did what we would now call basic algebra in geometrical terms, Diophantus did what we would now call basic algebraic geometry in purely algebraic terms. In modern language, what Diophantus does is to find rational parametrisations of many varieties; in other words, he shows how to obtain infinitely many rational numbers satisfying a system of equations by giving a procedure that can be made into an algebraic expression
(say,
, 
, 
,
where
, 
and 
are polynomials
or quotients of polynomials; this would be what is sought for if such
satisfied
a given equation
(say) for all values of r and s).
Diophantus also studies the equations of some non-rational curves, for which no rational parametrisation is possible. He manages to find some rational points on these curves – elliptic curves, as it happens, in what seems to be their first known occurrence—by means of what amounts to a tangent construction: translated into coordinate geometry
(which did not exist in Diophantus's time), his method would be visualised as drawing a tangent to a curve at a known
rational point, and then finding the other point of intersection of the tangent with the curve; that other point is a new
rational point. (Diophantus also resorts to what could be called a special case of a secant construction.)
While Diophantus is concerned largely with rational solutions, he assumes some results on integer numbers; in particular, he seems to assume that every integer is the sum of four squares, though he never states as much explicitly.
probably influenced Indian learning, to the point of introducing
trigonometry, it seems
to be the case that Indian mathematics is otherwise an indigenous
tradition;
in particular, there is no evidence that Euclid's Elements reached India
before the 18th century.
Āryabhaṭa
(476–550 CE) showed that pairs of simultaneous congruences
,
could be solved by a method he called kuṭṭaka, or pulveriser; this is a procedure close to (a generalisation of) the Euclidean algorithm
, which was probably discovered
independently in India. Āryabhaṭa seems to have had in mind applications to astronomical calculations.
Brahmagupta
(628 CE) started the systematic study of indefinite quadratic equations—in particular, the misnamed
Pell equation
, in which Archimedes
may have first been interested, and which did not start to be solved in the West until the time
of Fermat and Euler. Later Sanskrit authors would
follow, using Brahmagupta's technical terminology. A general procedure (the chakravala
, or "cyclic method") for solving Pell's equation was
finally found by Jayadeva (cited in the eleventh century; his work is otherwise lost); the earliest surviving exposition appears in Bhāskara II's
Bīja-gaṇita (twelfth century).
Unfortunately, Indian mathematics remained largely unknown in the West until the late eighteenth century; Brahmagupta and Bhāskara's work was translated (into English, by Colebrooke
) in 1817.
ordered translations of many Greek mathematical works and at least one Sanskrit work (the Sindhind,
which may or may not
be Brahmagupta
's Brāhmasphuţasiddhānta
), thus giving rise to the rich tradition of Islamic mathematics
.
Diophantus's main work, the Arithmetica, was translated into Arabic by Qusta ibn Luqa
(820–912).
Part of the treatise al-Fakhri (by al-Karajī
, 953 – ca. 1029) builds on it to some extent. Al-Karajī's contemporary Ibn al-Haytham knew what would later be called Wilson's theorem, which, arguably, was thus the first clearly non-trivial result on congruences to prime moduli ever known.
Other than a treatise on squares in arithmetic progression by
Fibonacci
– who lived and studied in north Africa and Constantinople during his formative
years, ca. 1175–1200 – no number theory to speak of was done in western Europe while it went through the Middle Ages.
Matters started to change in Europe in the late Renaissance
, thanks to a renewed study of the works of Greek antiquity.
A key catalyst was the textual emendation and translation into Latin of Diophantus's Arithmetica
(Bachet
, 1621, following a first attempt by Xylander
, 1575).
Pierre de Fermat
(1601–1665) never published his writings; in particular, his work on number theory is contained entirely in letters to mathematicians and in private marginal notes. He wrote down nearly no proofs in
number theory; he had
no models in the area. He did make repeated use of mathematical induction
, introducing the method of infinite descent
.
One of Fermat's first interests was perfect numbers (which appear in Euclid, Elements IX) and amicable numbers;
this led him to work on integer divisor
s, which were from the beginning among the subjects of the
correspondence (1636 onwards) that put him in touch with the mathematical community of the day. He had already studied Bachet's edition of Diophantus carefully; by 1643, his interests had shifted largely to diophantine problems and sums of squares (also treated by Diophantus).
Fermat's achievements in arithmetic include:
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
devoted primarily to the study of the integers. Number theorists study prime numbers (which, when multiplied, give all the integers) as well
as the properties of objects made out of integers (such as rational numbers) or defined as generalizations of the integers (such as, for example, algebraic integers).
Integers can be considered either in themselves or as solutions to equations
(diophantine geometry
Diophantine geometry
In mathematics, diophantine geometry is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry over a ground field K that is not algebraically closed, such as the field of rational numbers or a finite field, or more general...
). Questions in number theory are often best understood through
the study of analytical
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
objects (e.g., the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
). One may also study real numbers in relation to rational numbers, e.g., as approximated by the latter (diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
).
The older term for number theory is arithmetic; by the early twentieth century, it had been superseded by "number theory". (The word "arithmetic" is used by the general public to mean "elementary calculations"; it has also acquired other meanings in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, as in Peano arithmetic, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, as in floating point arithmetic
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
.) The use of the term arithmetic for number theory regained some ground in the second half of the 20th century, arguably in part due to French influence. In particular, arithmetical is preferred as an adjective to number-theoretic.
The dawn of arithmetic
The first historicalfind of an arithmetical nature is a fragment of a table: the broken clay tablet
Plimpton 322
Plimpton 322
Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University...
(Larsa, Mesopotamia, ca. 1800 BCE) contains a list of "Pythagorean triples", i.e., integers
such that .The triples are too many and too large to have been obtained by brute force.
The heading over the first column reads: "The takiltum of the diagonal which has been substracted such that the width..."
The table's outlay suggests that it was constructed by means of what amounts, in modern language, to the identity
which is implicit in routine Old Babylonian exercises. If some other method was used, the triples were first
constructed and then reordered by
, presumably for actual use as a "table",i.e., with a view to applications.
We do not know what these applications may have been, or whether there could have been any; Babylonian astronomy, for example, truly flowered only later. It has been suggested instead that the table was a source of numerical examples for school problems.
While Babylonian number theory – or what survives of Babylonian mathematics that can be called thus – consists of this single, striking fragment,
Babylonian algebra (in the
secondary-school sense of "algebra") was exceptionally well developed. Late Neoplatonic sources state that Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
learned mathematics from the Babylonians. (Much earlier sources state that Thales
Thales
Thales of Miletus was a pre-Socratic Greek philosopher from Miletus in Asia Minor, and one of the Seven Sages of Greece. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition...
and Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
travelled and studied in Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
.)
Euclid IX 21—34
is very probably Pythagorean; it is very simple material
("odd times even is odd", "if an odd number measures [= divides] an even number, then it also measures [= divides] half of it"), but it is all that is needed to prove that
is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. (Pythagoraean mystics gave great importance to the odd and the even.)
The discovery that
is irrational is creditedto the early Pythagoreans (pre-Theodorus
Theodorus of Cyrene
Theodorus of Cyrene was a Greek mathematician of the 5th century BC. The only first-hand accounts of him that we have are in two of Plato's dialogues: the Theaetetus and the Sophist...
). By revealing (in modern
terms) that numbers could be irrational, this discovery seems to have
provoked the first foundational crisis in mathematical history; its proof or its divulgation
are sometimes credited to Hippasus, who was expelled or split from
the Pythagorean sect. It is only here that we can start to speak of a clear, conscious division between
numbers (integers and the rationals – the subjects of arithmetic) and lengths (real numbers, whether rational or not).
The Pythagorean tradition spoke also of so-called polygonal
Polygonal number
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
or figured numbers. While square numbers, cubic numbers, etc., are seen now as more natural than triangular numbers, square numbers, pentagonal numbers, etc., the study of the sums
of triangular and pentagonal numbers would prove fruitful in the early modern period (17th to early 19th century).
We know of no clearly arithmetical material in ancient Egyptian
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
or Vedic
Vedic
Vedic may refer to:* the Vedas, the oldest preserved Indic texts** Vedic Sanskrit, the language of these texts** Vedic period, during which these texts were produced** Vedic pantheon of gods mentioned in Vedas/vedic period...
sources, though there is some algebra in both. The Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
appears as an exercise in Sun Zi
Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
's Suan Ching (also known as Sun Tzu's Mathematical Classic; 3rd, 4th or 5th century CE.). (There is one important step glossed over in Sun Zi's solution: it is the problem that was later solved by Āryabhaṭa
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
's kuṭṭaka – see below.)
There is also some numerical mysticism in Chinese mathematics, but, unlike that of the Pythagoreans, it seems to have
led nowhere. Like the Pythagoreans' perfect numbers, magic squares have passed from superstition into recreation.
Classical Greece and the early Hellenistic period
Aside from a few fragments, the mathematics of Classical Greece is known to us either through the reports of contemporary non-mathematicians or through mathematical works from the early Hellenistic period. In the case of number theory, thismeans, by and large, Plato and Euclid, respectively.
Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
had a keen interest in mathematics, and distinguished clearly between arithmetic and calculation. (By arithmetic he meant, in part, theorising on number, rather than what arithmetic or number theory have come to mean.) It is through one of Plato's dialogues—namely,
Theaetetus
Theaetetus (dialogue)
The Theaetetus is one of Plato's dialogues concerning the nature of knowledge. The framing of the dialogue begins when Euclides tells his friend Terpsion that he had written a book many years ago based on what Socrates had told him of a conversation he'd had with Theaetetus when Theaetetus was...
– that we know that Theodorus
Theodorus of Cyrene
Theodorus of Cyrene was a Greek mathematician of the 5th century BC. The only first-hand accounts of him that we have are in two of Plato's dialogues: the Theaetetus and the Sophist...
had proven that
are irrational. Theaetetus was, like Plato, a disciple of Theodorus's; he worked on distinguishing different kind of inconmensurables, and was thus arguably a pioneer in the study of number systems. (Book X of Euclid's ElementsEuclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
is described by Pappus
Pappus of Alexandria
Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
as being largely based on Theaetetus's work.)
Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
devoted part of his Elements to prime numbers and divisibility, topics that belong unambiguously to number theory and are basic thereto (Books VII to IX of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
).
In particular, he gave an algorithm for computing the greatest common divisor of two numbers
(the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
; Elements, Prop. VII.2) and the first known proof of the infinitude of primes (Elements, Prop. IX.20).
In 1773, Lessing
Gotthold Ephraim Lessing
Gotthold Ephraim Lessing was a German writer, philosopher, dramatist, publicist, and art critic, and one of the most outstanding representatives of the Enlightenment era. His plays and theoretical writings substantially influenced the development of German literature...
published an epigram
Epigram
An epigram is a brief, interesting, usually memorable and sometimes surprising statement. Derived from the epigramma "inscription" from ἐπιγράφειν epigraphein "to write on inscribe", this literary device has been employed for over two millennia....
he had found in a manuscript during his work as a librarian; it claimed to be a letter sent by Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
to Eratosthenes
Eratosthenes
Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
. The epigram proposed what has become known as
Archimedes' cattle problem
Archimedes' cattle problem
Archimedes' cattle problem is a problem in Diophantine analysis, the study of polynomial equations with integer solutions. Attributed to Archimedes, the problem involves computing the number of cattle in a herd of the sun god from a given set of restrictions...
; its solution (absent from the manuscript) requires solving an indeterminate quadratic equation (which reduces to what would later be misnamed Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
). As far as we know, such equations were first successfully treated by the Indian school. It is not known whether Archimedes himself had a method of solution.
Diophantus
of Diophantus's Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
survive in the original Greek; four more books survive in an Arabic translation. The Arithmetica is a collection of worked-out problems where the task is invariably to find rational solutions to a system of polynomial equations, usually of the form
or . Thus, nowadays, we speak of Diophantine equations when we speak of polynomial equations to which rational or integer solutions must be found.One may say that Diophantus was studying rational points—i.e., points whose coordinates are rational—on curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s and varieties
Variety
- Mathematics :* Abelian variety, a complex torus that can be embedded into projective space* Abstract variety, an intrinsically defined variety* Algebraic variety, the basic object of study in algebraic geometry** Affine variety, a subset of algebraic varieties...
; however, unlike the Greeks of the Classical period, who did what we would now call basic algebra in geometrical terms, Diophantus did what we would now call basic algebraic geometry in purely algebraic terms. In modern language, what Diophantus does is to find rational parametrisations of many varieties; in other words, he shows how to obtain infinitely many rational numbers satisfying a system of equations by giving a procedure that can be made into an algebraic expression
(say,
, , ,where
, and are polynomialsor quotients of polynomials; this would be what is sought for if such
satisfieda given equation
(say) for all values of r and s).Diophantus also studies the equations of some non-rational curves, for which no rational parametrisation is possible. He manages to find some rational points on these curves – elliptic curves, as it happens, in what seems to be their first known occurrence—by means of what amounts to a tangent construction: translated into coordinate geometry
(which did not exist in Diophantus's time), his method would be visualised as drawing a tangent to a curve at a known
rational point, and then finding the other point of intersection of the tangent with the curve; that other point is a new
rational point. (Diophantus also resorts to what could be called a special case of a secant construction.)
While Diophantus is concerned largely with rational solutions, he assumes some results on integer numbers; in particular, he seems to assume that every integer is the sum of four squares, though he never states as much explicitly.
The Indian school: Āryabhaṭa, Brahmagupta, Bhāskara
While Greek astronomy – thanks to Alexander's conquests –probably influenced Indian learning, to the point of introducing
trigonometry, it seems
to be the case that Indian mathematics is otherwise an indigenous
tradition;
in particular, there is no evidence that Euclid's Elements reached India
before the 18th century.
Āryabhaṭa
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
(476–550 CE) showed that pairs of simultaneous congruences
, could be solved by a method he called kuṭṭaka, or pulveriser; this is a procedure close to (a generalisation of) the Euclidean algorithmEuclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
, which was probably discovered
independently in India. Āryabhaṭa seems to have had in mind applications to astronomical calculations.
Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
(628 CE) started the systematic study of indefinite quadratic equations—in particular, the misnamed
Pell equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
, in which Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
may have first been interested, and which did not start to be solved in the West until the time
of Fermat and Euler. Later Sanskrit authors would
follow, using Brahmagupta's technical terminology. A general procedure (the chakravala
Chakravala method
The chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
, or "cyclic method") for solving Pell's equation was
finally found by Jayadeva (cited in the eleventh century; his work is otherwise lost); the earliest surviving exposition appears in Bhāskara II's
Bīja-gaṇita (twelfth century).
Unfortunately, Indian mathematics remained largely unknown in the West until the late eighteenth century; Brahmagupta and Bhāskara's work was translated (into English, by Colebrooke
Henry Thomas Colebrooke
Henry Thomas Colebrooke was an English orientalist.-Biography:Henry Thomas Colebrooke, third son of Sir George Colebrooke, 2nd Baronet, was born in London. He was educated at home; and when only fifteen he had made considerable attainments in classics and mathematics...
) in 1817.
Arithmetic in the Islamic golden age
In the early ninth century, the caliph Al-Ma'munAl-Ma'mun
Abū Jaʿfar Abdullāh al-Māʾmūn ibn Harūn was an Abbasid caliph who reigned from 813 until his death in 833...
ordered translations of many Greek mathematical works and at least one Sanskrit work (the Sindhind,
which may or may not
be Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's Brāhmasphuţasiddhānta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
), thus giving rise to the rich tradition of Islamic mathematics
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
.
Diophantus's main work, the Arithmetica, was translated into Arabic by Qusta ibn Luqa
Qusta ibn Luqa
Qusta ibn Luqa was a Melkite physician, scientist and translator, of Byzantine Greek extraction. He was born in Baalbek. Travelling to parts of the Byzantine Empire, he brought back Greek texts and translated them into Arabic.- Biography :Qusta ibn Luqa al-BaBa'albakki, i. e...
(820–912).
Part of the treatise al-Fakhri (by al-Karajī
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
, 953 – ca. 1029) builds on it to some extent. Al-Karajī's contemporary Ibn al-Haytham knew what would later be called Wilson's theorem, which, arguably, was thus the first clearly non-trivial result on congruences to prime moduli ever known.
Other than a treatise on squares in arithmetic progression by
Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
– who lived and studied in north Africa and Constantinople during his formative
years, ca. 1175–1200 – no number theory to speak of was done in western Europe while it went through the Middle Ages.
Matters started to change in Europe in the late Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
, thanks to a renewed study of the works of Greek antiquity.
A key catalyst was the textual emendation and translation into Latin of Diophantus's Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
(Bachet
Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...
, 1621, following a first attempt by Xylander
Guilielmus Xylander
Wilhelm Xylander was a German classical scholar and humanist....
, 1575).
Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
(1601–1665) never published his writings; in particular, his work on number theory is contained entirely in letters to mathematicians and in private marginal notes. He wrote down nearly no proofs in
number theory; he had
no models in the area. He did make repeated use of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, introducing the method of infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
.
One of Fermat's first interests was perfect numbers (which appear in Euclid, Elements IX) and amicable numbers;
this led him to work on integer divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s, which were from the beginning among the subjects of the
correspondence (1636 onwards) that put him in touch with the mathematical community of the day. He had already studied Bachet's edition of Diophantus carefully; by 1643, his interests had shifted largely to diophantine problems and sums of squares (also treated by Diophantus).
Fermat's achievements in arithmetic include:
- Fermat's little theoremFermat's little theoremFermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
(1640), stating that, if a is not divisible by a prime p, then
- If a and b are coprime, then
is not divisible by any prime congruent to −1 modulo 4. Every prime congruent to −1 modulo 4 can be written in the form 
. These statements date from 1640; in 1659, Fermat stated to Huygens that he had proven the latter statement by the method of descent. Fermat and Frenicle also did some work (some of it erroneous or non-rigorous) on other quadratic forms. - Fermat posed the problem of solving
as a challenge to English mathematicians (1657). The problem was solved in a few months by Wallis and Brouncker. Fermat considered their solution valid, but pointed out they had provided an algorithm without a proof (as had Jayadeva and Bhaskara, though Fermat would never know this). He states that a proof can be found by descent. - Fermat developed methods for (doing what in our terms amounts to) finding points on curves of genusGenusIn biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...
0 and 1. As in Diophantus, there are many special procedures and what amounts to a tangent construction, but no use of a secant construction. - Fermat states and proves in his correspondence that
has no non-trivial solutions in the integers. Fermat also mentioned to his correspondents that 
has no non-trivial solutions, and that this could be proven by descent. The first known proof is due to Euler (1753; indeed by descent).
Fermat's claim ("Fermat's last theoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
") to have shown there are no solutions to
for all 
(a fact completely beyond his methods) appears only on his annotations on the margin of his copy of Diophantus; he never claimed this to others and thus had no need to retract it if he found a mistake in his alleged proof.
Euler
The interest of Leonhard Euler
Leonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(1707–1783) in number theory was first spurred in 1729, when a friend of his, the amateur GoldbachChristian GoldbachChristian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...
, pointed him towards some of Fermat's work on the subject. This has been called the "rebirth" of modern number theory, after Fermat's relative lack of success in getting his contemporaries' attention for the subject. Euler's work on number theory includes the following:
- Proofs for Fermat's statements. This includes Fermat's little theoremFermat's little theoremFermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
(generalised by Euler to non-prime moduli); the fact that
if and only if 
; initial work towards a proof that every integer is the sum of four squares (the first complete proof is by LagrangeLagrangeLa Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
(1770), soon improved by Euler himself); the lack of non-zero integer solutions to
(implying the case n=4 of Fermat's last theorem, the case n=3 of which Euler also proved by a related method).
- Pell's equationPell's equationPell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
, first misnamed by Euler. He wrote on the link between continued fractions and Pell's equation. - First steps towards analytic number theoryAnalytic number theoryIn mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
. In his work of sums of four squares, partitions, pentagonal numbers, and the distribution of prime numbers, Euler pioneered the use of what can be seen as analysis (in particular, infinite series) in number theory. Since he lived before the development of complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, most of his work is restricted to the formal manipulation of power series. He did, however, do some very notable (though not fully rigorous) early work on what would later be called the Riemann zeta function. - Quadratic forms. Following Fermat's lead, Euler did further research on the question of which primes are can be expressed in the form
, some of it prefiguring quadratic reciprocity. - Diophantine equations. Euler worked on some diophantine equations of genus 0 and 1. In particular, he studied DiophantusDiophantusDiophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
's work; he tried to systematise it, but the time was not yet ripe for such an endeavour – algebraic geometry was still in its infancy. He did notice there was a connection between diophantine problems and elliptic integrals, whose study he had himself initiated.
Lagrange, Legendre and Gauss
Lagrange
LagrangeLa Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
(1736–1813) was the first to give full proofs of some of Fermat's and Euler's work and observations
- for instance,
the four-square theoremLagrange's four-square theoremLagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
and the basic theory of the misnamed "Pell's equation" (for which an algorithmic solution was found by Fermat and his contemporaries, and also by Jayadeva and Bhaskara II before them). He also studied quadratic forms in full generality (as opposed to
) -- defining their equivalence relation, showing how to put them in reduced form, etc.
LegendreAdrien-Marie LegendreAdrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
(1752–1833) was the first to state the law of quadratic reciprocity. He also
conjectured what amounts to the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
and Dirichlet's theorem on arithmetic progressionsDirichlet's theorem on arithmetic progressionsIn number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
. He gave a full treatment of the equation
and worked on quadratic forms along the lines later developed fully by Gauss. In his old age, he was the first to prove "Fermat's last theorem" for 
(completing work by Dirichlet, and crediting both him and Sophie GermainSophie GermainMarie-Sophie Germain was a French mathematician, physicist, and philosopher. Despite initial opposition from her parents and difficulties presented by a gender-biased society, she gained education from books in her father's library and from correspondence with famous mathematicians such as...
).
In Disquisitiones Arithmeticae
Disquisitiones ArithmeticaeThe Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
(1798), GaussGaussGauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
(1777–1855) proved the law of quadratic reciprocityQuadratic reciprocityIn number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
and developed the theory of quadratic forms (in particular, defining their composition). He also introduced some basic notation (congruences) and devoted a section to computational matters, including primality tests. The last section of the Disquisitiones established a link between roots of unity and number theory:
The theory of the division of the circle…which is treated in sec. 7 does not belong
by itself to arithmetic, but its principles can only be drawn from higher arithmetic.
In this way, Gauss arguably made a first foray towards both Galois's work and algebraic number theoryAlgebraic number theoryAlgebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
Maturity. Division into subfields.
Starting early in the nineteenth century, the following developments gradually took place:
- The rise to self-consciousness of number theory (or higher arithmetic) as a field of study.
- The development of much of modern mathematics necessary for basic modern number theory: complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, Galois theoryGalois theoryIn mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
—accompanied by greater rigor in analysis and abstraction in algebra. - The rough subdivision of number theory into its modern subfields—in particular, analyticAnalytic number theoryIn mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
and algebraic number theoryAlgebraic number theoryAlgebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
Algebraic number theory may be said to start with the study of reciprocity and cyclotomy, but truly came into its own with the development of abstract algebra and early ideal theory and valuation theory; see below. A conventional starting point for analytic number theory is Dirichlet's theorem on arithmetic progressionsDirichlet's theorem on arithmetic progressionsIn number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
(1837), whose proof introduced L-functions and involved some asymptotic analysis and a limiting process on a real variable. The first use of analytic ideas in number theory actually
goes back to Euler (1730s), who used formal power series and non-rigorous (or implicit) limiting arguments. The use of complex analysis in number theory comes later: the work of Riemann (1859) on the zeta function is the canonical starting point; Jacobi's four-square theoremJacobi's four-square theoremIn 1834, Carl Gustav Jakob Jacobi found an exact formula for the total number of ways a given positive integer n can be represented as the sum of four squares...
(1839), which predates it, belongs to an initially different strand that has by now taken a leading role in analytic number theory (modular forms).
The history of each subfield is briefly addressed in its own section below; see the main article of each subfield for fuller treatments. Many of the most interesting questions in each area remain open and are being actively worked on.
Elementary tools
The term elementaryElementary proofIn mathematics, an elementary proof is a mathematical proof that only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be...
generally denotes a method that does not use complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. For example, the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
was first proven in 1896, but an elementary proof was found only in 1949 by ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
. The term is somewhat ambiguous: for example, proofs based on complex Tauberian theorems (e.g. Wiener–Ikehara) are often seen as quite enlightening but not elementary, in spite of using Fourier analysis, rather than complex analysis as such. Here as elsewhere, an elementary proof may be longer and more difficult for most readers than a non-elementary one.
Number theory has the reputation of being a field many of whose results can be stated to the layperson. At the same time, the proofs of these results are not particularly accessible, in part because the range of tools they use is, if anything, unusually broad within mathematics.
Analytic number theory
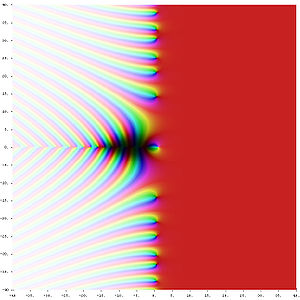Analytic number theory may be defined
- in terms of its tools, as the study of the integers by means of tools from real and complex analysis,
- in terms of its concerns, as the study within number theory of estimates on size and density, as opposed to identities.
Some subjects generally considered to be part of analytic number theory, e.g., sieve theorySieve theorySieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
, are better covered by the second rather than the first definition: some of sieve theory, for instance, uses little analysis, yet it is considered to be part of
analytic number theory.
The following are examples of problems in analytic number theory: the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, the Goldbach conjecture (or the twin prime conjecture, or the Hardy–Littlewood conjectures), the Waring problem and the Riemann HypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. Some of the most important tools of analytic number theory are the circle method, sieve methods and L-functions (or, rather, the study of their properties). The theory of modular forms (and, more generally, automorphic forms) also occupies an increasingly central place in the toolbox of analytic number theory.
One may ask analytic questions about algebraic numbers, and use analytic means to answer such questions; it is thus that algebraic and analytic number theory intersect. For example, one may define prime ideals (generalizations of prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s living in the field of algebraic numbers) and ask how many prime ideals there are up to a certain size. This question can be answered by means of an examination of Dedekind zeta functionDedekind zeta functionIn mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
s, which are generalizations of the Riemann zeta function, an all-important analytic object that describes the distribution of prime numbers.
Algebraic number theory
Algebraic number theory studies algebraic properties and algebraic objects of interest in number theory. (Thus, analytic and algebraic number theory can and do overlap:
the former is defined by its methods, the latter by its objects of study.)
A key topic is that of the algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, which are generalizations of the rational numbers. Briefly, an algebraic number is any complex number that is a solution to some polynomial equation
with rational coefficients;
for example, every solution
of 
(say) is an algebraic number. Fields of algebraic numbers are also called algebraic number fieldAlgebraic number fieldIn mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s, or shortly number fields.
It could be argued that the simplest kind of number fields (viz., quadratic fields) were already studied by Gauss, as the discussion of quadratic forms in Disquisitiones arithmeticae can be restated in terms of idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s and
normsNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
in quadratic fields. (A quadratic field consists of all
numbers of the form
, where
and 
are rational numbers and 
is a fixed rational number whose square root is not rational.)
For that matter, the 11th-century chakravala methodChakravala methodThe chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
amounts—in modern terms—to an algorithm for finding the units of a real quadratic number field. However, neither Bhāskara nor Gauss knew of number fields as such.
The grounds of the subject as we know it were set in the late nineteenth century, when ideal numbers, the theory of ideals and valuation theory were developed; these are three complementary ways of dealing with the lack of unique factorisation in algebraic number fields. (For example, in the field generated by the rationals
and
, the number 
can be factorised both as 
and
; all of 
, 
, 
and
are irreducible, and thus, in a naïve sense, analogous to primes among the integers.)
The initial impetus for the development of ideal numbers (by KummerErnst KummerErnst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
) seems to have come from the study
of higher reciprocity laws, i.e., generalisations of quadratic reciprocityQuadratic reciprocityIn number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
.
Number fields are often studied as extensions of smaller number fields: a field L is said to be an extension of a field K if L contains K.
(For example, the complex numbers C are an extension of the reals R,
and the reals R are an extension of the rationals Q.)
Classifying the possible extensions of a given number field is a difficult and partially open problem. Abelian extensions—that is, extensions L of K such that the Galois groupGalois groupIn mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
Gal(L/K) of L over K is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
—are relatively well understood.
Their classification was the object of the programme of class field theoryClass field theoryIn mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, which was initiated in the late 19th century (partly by Kronecker and Eisenstein) and carried out largely in 1900—1950.
An example of an active area of research in algebraic number theory is Iwasawa theoryIwasawa theoryIn number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
. The Langlands programLanglands programThe Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
, one of the main current large-scale research plans in mathematics, is sometimes described as an attempt to generalise class field theory to non-abelian extensions of number fields.
Diophantine geometry
The central problem of Diophantine geometry is to determine when a Diophantine equationDiophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
has solutions, and if it does, how many. The approach taken is to think of the solutions of an equation as a geometric object.
For example, an equation in two variables defines a curve in the plane. More generally, an equation, or system of equations, in two or more variables defines a curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, a surfaceAlgebraic surfaceIn mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
or some other such object in n-dimensional space. In Diophantine geometry, one asks whether there are any rational points (points all of whose coordinates are rationals) or
integral points (points all of whose coordinates are integers) on the curve or surface. If there are any such points, the next step is to ask how many there are and how they are distributed. A basic question in this direction is: are there finitely
or infinitely many rational points on a given curve (or surface)? What about integer points?
An example here may be helpful. Consider the Pythagorean equationPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
;
we would like to study its rational solutions, i.e., its solutions
such that
x and y are both rational. This is the same as asking for all integer solutions
to
; any solution to the latter equation gives
us a solution
, 
to the former. It is also the
same as asking for all points with rational coordinates on the curve
described by
. (This curve happens to be a circle of radius 1 around the origin.)
The rephrasing of questions on equations in terms of points on curves turns out to be felicitous. The finiteness or not of the number of rational or integer points on an algebraic curve—that is, rational or integer solutions to an equation
, where 
is a polynomial in two variables—turns out to depend crucially on the genus of the curve. The genus can be defined as follows: allow the variables in 
to be complex numbers; then 
defines a 2-dimensional surface in (projective) 4-dimensional space (since two complex variables can be decomposed into four real variables, i.e., four dimensions). Count
the number of (doughnut) holes in the surface; call this number the genus of
. Other geometrical notions turn out to be just as crucial.
There is also the closely linked area of diophantine approximations: given a number
, how well can it be approximated by rationals? (We are looking for approximations that are good relative to the amount of space that it takes to write the rational: call 
(with 
) a good approximation to 
if 
, where 
is large.) This question is of special interest if 
is an algebraic number. If 
cannot be well approximated, then some equations do not have integer or rational solutions. Moreover, several concepts (especially that of heightHeightHeight is the measurement of vertical distance, but has two meanings in common use. It can either indicate how "tall" something is, or how "high up" it is. For example "The height of the building is 50 m" or "The height of the airplane is 10,000 m"...
) turn out to be crucial both in diophantine geometry and in the study of diophantine approximations.
Diophantine geometry should not be confused with the geometry of numbersGeometry of numbersIn number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by ....
, which is a collection of graphical methods for answering certain questions in algebraic number theory. Arithmetic geometry, on the other hand, is a contemporary term
for much the same domain as that covered by the term diophantine geometry. The term arithmetic geometry is arguably used
most often when one wishes to emphasise the connections to modern algebraic geometry (as in, for instance, Faltings' theoremFaltings' theoremIn number theory, the Mordell conjecture is the conjecture made by that a curve of genus greater than 1 over the field Q of rational numbers has only finitely many rational points. The conjecture was later generalized by replacing Q by a finite extension...
) rather than to techniques in diophantine approximations.
Recent approaches and subfields
The areas below date as such from no earlier than the mid-twentieth century, even if they are based on older material. For example, as is explained below, the matter of algorithms in number theory is very old, in some sense older than the concept of proof; at the same time, the modern study of computability dates only from the 1930s and 1940s, and computational complexityComputational ComplexityComputational Complexity may refer to:*Computational complexity theory*Computational Complexity...
from the 1970s.
Probabilistic number theory
Take a number at random between one and a million. How likely is it to be prime? This is just another way of asking how many primes there are between one and a million. Very well; ask further: how many prime divisors will it have, on average? How many divisors will it have altogether, and with what likelihood? What is the probability that it have many more or many fewer divisors or prime divisors than the average?
Much of probabilistic number theory can be seen as an important special case of the study of variables that are almost, but not quite, mutually independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. For example, the event that a random integer between one and a million be divisible by two and the event that it be divisible by three are almost independent, but not quite.
It is sometimes said that probabilistic combinatorics uses the fact that whatever happens with probability greater than
must happen sometimes; one may say with equal justice that many applications of probabilistic number theory hinge on the fact that whatever is unusual must be rare. If certain algebraic objects (say, rational or integer solutions to certain equations) can be shown to be in the tail of certain sensibly defined distributions, it follows that there must be few of them; this is a very concrete non-probabilistic statement following from a probabilistic one.
At times non-rigorous, probabilistic approach leads to a number of heuristicHeuristicHeuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
algorithms and open problems, notably Cramér's conjecture.
Arithmetic combinatorics
Let
be a set of integers. Consider the set 
consisting of all sums of two elements of 
. Is 
much larger than A? Barely larger? If 
is barely larger than 
, must 
have plenty of arithmetic structure \pmod e.g., does it look like an arithmetic progressionArithmetic progressionIn mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
?
If we begin from a fairly "thick" infinite set
, does it contain many elements in arithmetic progression: 
,
, 
, 
, 
, 
, say? Should it be possible to write large integers as sums of elements of 
?
These questions are characteristic of arithmetic combinatorics. This is a presently coalescing field; it subsumes additive number theoryAdditive number theoryIn number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
(which concerns itself with certain very specific sets
of arithmetic significance, such as the primes or the squares) and, arguably, some of the geometry of numbersGeometry of numbersIn number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by ....
,
together with some rapidly developing new material. Its focus on issues of growth and distribution accounts in part for its developing links with ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, finite group theory, model theoryModel theoryIn mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, and other fields. The term additive combinatorics is also used; however, the sets
being studied need not be sets of integers, but rather subsets of non-commutative groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, for which the multiplication symbol, not the addition symbol, is traditionally used; they can also be subsets of ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s, in which case the growth of
and 
·
may be
compared.
Computations in number theory
While the word algorithm goes back only to certain readers of al-Khwārizmī, careful descriptions of methods of solution are older than proofs: such methods (that is, algorithms) are as old as any recognisable mathematics—ancient Egyptian, Babylonian, Vedic, Chinese—whereas proofs appeared only with the Greeks of the classical period.
An interesting early case is that of what we now call the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
. In its basic form (namely, as an algorithm for computing the greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
) it appears as Proposition 2 of Book VII in ElementsEuclid's ElementsEuclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, together with a proof of correctness. However, in the form that is often used in number theory (namely, as an algorithm for finding integer solutions to an equation
,
or, what is the same, for finding the quantities whose existence is assured by the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
) it first appears in the works of Āryabhaṭa (5th–6th century CE) as an algorithm called
kuṭṭaka ("pulveriser"), without a proof of correctness.
There are two main questions: "can we compute this?" and "can we compute it rapidly?". Anybody can test whether a number is prime or, if it is not, split it into prime factors; doing so rapidly is another matter. We now know fast algorithms for testing primalityPrimality testA primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
, but, in spite of much work (both theoretical and practical), no truly fast algorithm for factoring.
The difficulty of a computation can be useful: modern protocols for encrypting messagesCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
(e.g., RSA) depend on functions that are known to all, but whose inverses (a) are known only to a chosen few, and (b) would take one too long a time to figure out on one's own. For example, these functions can be such that their inverses can be computed only if certain large integers are factorized. While many difficult computational problems outside number theory are known, most working encryption protocols nowadays are based on the difficulty of a few number-theoretical problems.
On a different note—some things may not be computable at all; in fact, this can be proven in some instances. For instance, in 1970, it was proven that there is no Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
which can solve all Diophantine equations (see Hilbert's 10th problem). There are thus some problems in number theory that will never be solved. We even know the shape of some of them, viz., Diophantine equations in nine variables; we simply do not know, and cannot know, which coefficients give us equations for which the following two statements are both true: there are no solutions, and we shall never know that there are no solutions.
Literature
Two of the most popular introductions to the subject are:
- G. H. Hardy and E. M. Wright, An introduction to the theory of numbers, 6th ed., rev. by D. R. Heath-Brown and J. H. Silverman, Oxford University Press, Oxford, 2008 (first published in 1938).
- I. M. VinogradovIvan Matveyevich VinogradovIvan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
, Elements of Number Theory, Mineola, NY: Dover Publications, 2003, reprint of the 1954 edition.
Hardy and Wright's book is a comprehensive classic, though its clarity sometimes suffers due to the authors' insistence on elementary methods.
Vinogradov's main attraction consists in its set of problems, which quickly lead to Vinogradov's own research interests; the text itself is very basic and close to minimal.
Popular choices for a second textbook include:- Jean-Pierre SerreJean-Pierre SerreJean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
, A Course in Arithmetic, Graduate Texts in MathematicsGraduate Texts in MathematicsGraduate Texts in Mathematics is a series of graduate-level textbooks in mathematics published by Springer-Verlag. The books in this series, like the other Springer-Verlag mathematics series, are yellow books of a standard size...
, Springer Verlag, (1996, ISBN 978-0-387-90040-7)
External links
- Pell's equation
- If a and b are coprime, then