
Cycloid
Encyclopedia
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.
It is an example of a roulette
, a curve generated by a curve rolling on another curve.
The cycloid is the solution to the brachistochrone problem (i.e. it is the curve of fastest descent under gravity) and the related tautochrone problem (i.e. the period of an object in descent without friction inside this curve does not depend on the object's starting position).
and later by Mersenne
. It was named by Galileo
in 1599. In 1634 G.P. de Roberval showed that the area under one arch of a cycloid is three times the area of its generating circle. In 1658 Christopher Wren
showed that the length of one arch of a cycloid is four times the diameter of its generating circle. The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th century mathematicians.
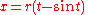
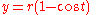
where t is a real parameter
, corresponding to the angle through which the rolling circle has rotated, measured in radian
s. For given t, the circle's centre lies at x = rt, y = r.
Solving for t and replacing, the Cartesian equation
would be

The first arch of the cycloid consists of points such that

The cycloid is differentiable everywhere except at the cusps
where it hits the x-axis, with the derivative tending toward or
or  as one approaches a cusp. The map from t to (x, y) is a differentiable curve
as one approaches a cusp. The map from t to (x, y) is a differentiable curve
or parametric curve of class C∞ and the singularity where the derivative is 0 is an ordinary cusp.
The cycloid satisfies the differential equation
:
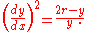
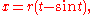
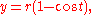
with

Since
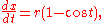
we find the area under the arch to be
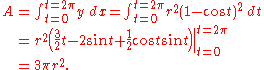
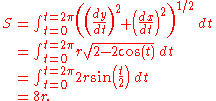
also traces a cycloid path. Such a cycloidal pendulum is isochronous
, regardless of amplitude.
The 17th Century Dutch mathematician Christiaan Huygens discovered and proved these properties of the cycloid in the search to the design of more accurate pendulum clocks for use in navigation.
All these curves are roulettes
with a circle rolled along a uniform curvature
. The cycloid, epicycloids, and hypocycloids have the property that each is similar
to its evolute
. If q is the product
of that curvature with the circle's radius, signed positive for epi- and negative for hypo-, then the curve:evolute similitude ratio is 1 + 2q.
The classic Spirograph
toy traces out hypotrochoid and epitrochoid
curves.
 The cycloidal arch was used by architect Louis Kahn
The cycloidal arch was used by architect Louis Kahn
in his design for the Kimbell Art Museum
in Fort Worth, Texas
. It was also used in the design of the Hopkins Center
in Hanover, New Hampshire
.
It is an example of a roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
, a curve generated by a curve rolling on another curve.
The cycloid is the solution to the brachistochrone problem (i.e. it is the curve of fastest descent under gravity) and the related tautochrone problem (i.e. the period of an object in descent without friction inside this curve does not depend on the object's starting position).
History
The cycloid was first studied by Nicholas of CusaNicholas of Cusa
Nicholas of Kues , also referred to as Nicolaus Cusanus and Nicholas of Cusa, was a cardinal of the Catholic Church from Germany , a philosopher, theologian, jurist, mathematician, and an astronomer. He is widely considered one of the great geniuses and polymaths of the 15th century...
and later by Mersenne
Marin Mersenne
Marin Mersenne, Marin Mersennus or le Père Mersenne was a French theologian, philosopher, mathematician and music theorist, often referred to as the "father of acoustics"...
. It was named by Galileo
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
in 1599. In 1634 G.P. de Roberval showed that the area under one arch of a cycloid is three times the area of its generating circle. In 1658 Christopher Wren
Christopher Wren
Sir Christopher Wren FRS is one of the most highly acclaimed English architects in history.He used to be accorded responsibility for rebuilding 51 churches in the City of London after the Great Fire in 1666, including his masterpiece, St. Paul's Cathedral, on Ludgate Hill, completed in 1710...
showed that the length of one arch of a cycloid is four times the diameter of its generating circle. The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th century mathematicians.
Equations
The cycloid through the origin, generated by a circle of radius r, consists of the points (x, y), with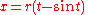
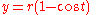
where t is a real parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
, corresponding to the angle through which the rolling circle has rotated, measured in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. For given t, the circle's centre lies at x = rt, y = r.
Solving for t and replacing, the Cartesian equation
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
would be

The first arch of the cycloid consists of points such that

The cycloid is differentiable everywhere except at the cusps
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
where it hits the x-axis, with the derivative tending toward
 or
or  as one approaches a cusp. The map from t to (x, y) is a differentiable curve
as one approaches a cusp. The map from t to (x, y) is a differentiable curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
or parametric curve of class C∞ and the singularity where the derivative is 0 is an ordinary cusp.
The cycloid satisfies the differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
:
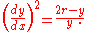
Area
One arch of a cycloid generated by a circle of radius r can be parameterized by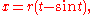
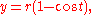
with

Since
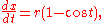
we find the area under the arch to be
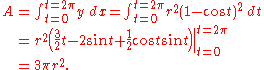
Arc length
The arc length S of one arch is given by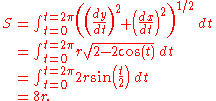
Cycloidal pendulum
If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the "string" is constrained between the adjacent arcs of the cycloid, and the pendulum's length is equal to that of half the arc length of the cycloid (i.e. twice the diameter of the generating circle), the bob of the pendulumPendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
also traces a cycloid path. Such a cycloidal pendulum is isochronous
Tautochrone curve
A tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point...
, regardless of amplitude.
The 17th Century Dutch mathematician Christiaan Huygens discovered and proved these properties of the cycloid in the search to the design of more accurate pendulum clocks for use in navigation.
Related curves
Several curves are related to the cycloid.- Curtate cycloid: Here the point tracing out the curve is inside the circle, which rolls on a line.
- Prolate cycloid: Here the point tracing out the curve is outside the circle, which rolls on a line.
- TrochoidTrochoidthumb|290px|right|A [[cycloid]] generated by a rolling circleTrochoid is the word created by Gilles de Roberval for the curve described by a fixed point as a circle rolls along a straight line...
: refers to any of the cycloid, the curtate cycloid and the prolate cycloid. - HypocycloidHypocycloidIn geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...
: The point is on the edge of the circle, which rolls not on a line but on the inside of another circle. - EpicycloidEpicycloidIn geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
: The point is on the edge of the circle, which rolls not on a line but on the outside of another circle. - HypotrochoidHypotrochoidA hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
: As hypocycloid but the point need not be on the edge of its circle. - EpitrochoidEpitrochoidAn epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
: As epicycloid but the point need not be on the edge of its circle.
All these curves are roulettes
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
with a circle rolled along a uniform curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. The cycloid, epicycloids, and hypocycloids have the property that each is similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to its evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
. If q is the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of that curvature with the circle's radius, signed positive for epi- and negative for hypo-, then the curve:evolute similitude ratio is 1 + 2q.
The classic Spirograph
Spirograph
Spirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced...
toy traces out hypotrochoid and epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
curves.
Use in architecture

Louis Kahn
Louis Isadore Kahn was an American architect, based in Philadelphia, Pennsylvania, United States. After working in various capacities for several firms in Philadelphia, he founded his own atelier in 1935...
in his design for the Kimbell Art Museum
Kimbell Art Museum
The Kimbell Art Museum in Fort Worth, Texas, hosts a small but excellent art collection as well as traveling art exhibitions, educational programs and an extensive research library. Its initial artwork came from the private collection of Kay and Velma Kimbell, who also provided funds for a new...
in Fort Worth, Texas
Fort Worth, Texas
Fort Worth is the 16th-largest city in the United States of America and the fifth-largest city in the state of Texas. Located in North Central Texas, just southeast of the Texas Panhandle, the city is a cultural gateway into the American West and covers nearly in Tarrant, Parker, Denton, and...
. It was also used in the design of the Hopkins Center
Hopkins Center for the Arts
Hopkins Center for the Creative and Performing Arts at Dartmouth College is located at 2 East Wheelock Street in Hanover, New Hampshire. The center, which was designed by Wallace K. Harrison and foreshadows his later design of Manhattan’s Lincoln Center, is the college’s cultural hub. It is home...
in Hanover, New Hampshire
Hanover, New Hampshire
Hanover is a town along the Connecticut River in Grafton County, New Hampshire, United States. The population was 11,260 at the 2010 census. CNN and Money magazine rated Hanover the sixth best place to live in America in 2011, and the second best in 2007....
.
See also
- EpicycloidEpicycloidIn geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
- EpitrochoidEpitrochoidAn epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
- HypocycloidHypocycloidIn geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...
- HypotrochoidHypotrochoidA hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
- SpirographSpirographSpirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced...
Other References
- An application from physics: Ghatak, A. & Mahadevan, L. Crack street: the cycloidal wake of a cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
tearing through a sheet. Physical Review Letters, 91, (2003). link.aps.org - Edward Kasner & James Newman (1940) Mathematics and the Imagination, pp 196–200, Simon & SchusterSimon & SchusterSimon & Schuster, Inc., a division of CBS Corporation, is a publisher founded in New York City in 1924 by Richard L. Simon and M. Lincoln Schuster. It is one of the four largest English-language publishers, alongside Random House, Penguin and HarperCollins...
.
External links
Retrieved April 27, 2007.- Cycloids at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- A Treatise on The Cycloid and all forms of Cycloidal Curves, monograph by Richard A. Proctor, B.A. posted by Cornell University Library.
- Cicloides y trocoides
- Cycloid Curves by Sean Madsen with contributions by David von Seggern, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Cycloid on PlanetPTC (Mathcad

